對于初學者來說，機器學習相當復雜，可能很容易迷失在細節的海洋里。本文通過將機器學習算法分為三個類別，梳理出一條相對清晰的路線，幫助初學者理解機器學習算法的基本原理，從而更高效地學習機器學習。 原文:Machine Learning in Three Steps: How to Efficiently Learn It[1]

當有志于成為數據科學家的學習者試圖學習機器學習算法時，通常會采用兩種極端方法。第一種方法是學習并從頭實現所有復雜算法，從而期待真正掌握這些算法。另一種方法假設計算機可以自己"學習"，因此個人沒有必要學習算法，從而導致一些人只依賴于諸如lazypredict之類的工具軟件包。

在學習機器學習算法時，比較現實的是在這兩個極端中間采取某種方法。不過還有問題，那就是從哪里開始呢？本文中我將把機器學習算法分為三類，并就從什么開始和可以跳過什么提供一些拙見。

機器學習算法的復雜性

由于可用算法眾多，開始學習機器學習可能很快就會被壓垮。線性回歸(linear regression)、支持向量機(SVM, support vector machine)、梯度下降(gradient descent)、梯度增強(gradient boosting)、決策樹(decision tree)、LASSO(Least Absolute Shrinkage and Selection Operator)、嶺回歸(ridge)、網格搜索(grid search)、等等，都是在提出這個問題時立馬能夠想到的一些算法。

在監督學習領域，這些算法有不同的目的和目標。本文只討論監督學習。

為了更好地理解各種技術，根據其目標和復雜度級別進行分類是有幫助的。通過將這些算法組織成不同類別和復雜度，可以簡化概念，使其更容易理解。這種方法可以極大增強人們對機器學習的理解，并幫助確定用于特定任務或目標的最合適的技術。

當學生深入研究機器學習領域時，可能會因為其復雜性而感到氣餒。然而，在付諸實踐之前，沒有必要學習或熟悉所有算法。機器學習領域的不同職位可能需要不同熟練程度，在某些方面缺乏知識是可以接受的。例如，數據科學家、數據分析師、數據工程師和機器學習研究人員這些不同的角色有不同的要求。

對整個過程有廣泛的理解可以使機器學習從業者在時間緊迫的情況下跳過某些技術細節，同時仍然理解整個過程。

1. 分解機器學習算法

1.1 模型、訓練和調優

"機器學習算法"的范圍相當廣泛，可以分為三種主要類型的算法：

用于接收輸入數據并隨后生成預測的機器學習模型，如線性回歸、支持向量機、決策樹、KNN等。

用于創建或優化模型的**模型訓練/擬合算法(model training/fitting algorithms)**，即為特定數據集找到模型的參數。不同的機器學習模型有其特定的訓練算法。雖然梯度下降是最著名的訓練基于數學函數的模型的方法，但其他機器學習模型可以使用不同的技術進行訓練，本文將在后面的部分中更詳細探討這些技術。

**超參數調優(hyperparameter tuning)**，即尋找機器學習模型的最優超參數。與訓練過程相反，超參數調優的過程通常不依賴于機器學習模型。盡管還有其他替代方法，但網格搜索是執行此任務的一種流行且常用的方法，我們將在本文后面深入討論。

1.2 三類ML模型

第一種類型涉及能夠接收數據并根據該數據生成預測的模型。這些模型可以分為三大類：

基于距離(Distance-based)的模型，包括K-近鄰(K-nearest-neighbors)、線性判別分析(Linear Discriminant Analysis)和二次判別分析(Quadratic Discriminant Analysis)。在scikit-learn庫中，這些也被稱為"估算器(estimators)"。

基于決策樹(Decision tree)的模型，例如單個決策樹(用于分類或回歸)、隨機森林(Random Forest)和梯度增強決策樹(Gradient-Boosted Decision Trees)。

基于數學函數(Mathematical functions)的模型，也被稱為參數模型，是假設輸入和輸出之間關系的特定函數形式的模型。可以進一步分為線性模型(linear model)，如OLS回歸、SVM(具有線性核)、Ridge和LASSO，以及非線性模型，如具有非線性核的SVM和神經網絡。

1.3 元模型和集成方法

在機器學習中，元模型(meta-model)是一種將多個個體模型的預測結果結合起來以獲得更準確預測的模型，也被稱為"堆疊模型(stacked model)"或"超級學習器(super learner)"。構成元模型的個體模型可以是不同類型的或使用不同算法，它們的預測結果可以通過加權平均或其他技術進行組合。

元模型的目標是通過減少個體模型可能存在的方差和偏差來提高預測的總體準確性和魯棒性，并且通過捕捉數據中更復雜的模式來克服個體模型的局限性。

常見的創建元模型的方法是基于集成的方法，比如打包(bagging)、增強(boosting)或堆疊(stacking)。

打包(Bagging)或Bootstrap Aggregating是一種通過組合基于數據集的不同樣本訓練多個模型來減少模型方差的機器學習技術。Bagging背后的思想是生成多個模型，每個模型都有一個數據子集，然后組合起來創建一個更健壯、更不易過擬合的模型。

增強(Boosting)是另一種集成方法，將多個弱模型組合在一起創建一個強模型。與Bagging不同的不同之處在于，Bagging是獨立訓練每個模型，而Boosting是按順序訓練模型，每個新模型都是在之前模型錯誤分類的數據上進行訓練，通過匯總所有模型的預測來完成最終的預測。

堆疊(Stacking)或堆疊泛化(stacked generalization)，是一種元模型集成方法，方法是訓練多個基本模型，并以基本模型的預測作為更高級模型的輸入，高級模型通過結合基本模型的預測來做出最終預測。

隨機森林(Random forests)是Bagging的延伸，增加了額外的隨機性。除了對數據進行隨機抽樣外，隨機森林還為每個分割隨機選擇特征子集，從而有助于減少過擬合并增加集合中模型的多樣性。

集成方法最常應用于決策樹，而非線性回歸等線性模型。這是因為決策樹比線性模型更容易出現過擬合，而集成方法通過組合多個模型有助于減少過擬合。

決策樹有高方差和低偏差，意味著容易過度擬合訓練數據，導致在新的、未見過的數據上表現不佳。集成方法通過聚合多個決策樹的預測來解決這個問題，從而產生更健壯和準確的模型。

另一方面，線性模型(如線性回歸)具有低方差和高偏差，意味著不太容易過度擬合，但可能造成欠擬合。集成方法對線性模型不那么有效，因為模型已經是低方差的，無法從聚合中獲益。

然而，在某些情況下，集成方法仍然可以應用于線性模型。例如，Bagging中使用的自舉聚合技術可以應用于任何類型模型，包括線性回歸。在這種情況下，Bagging算法會對訓練數據進行采樣，并在自舉樣本上擬合多個線性回歸模型，從而使模型更穩定、更具有魯棒性。然而，值得注意的是，得到的模型仍然是線性回歸模型，而不是元模型。

總的來說，雖然集成方法最常用于決策樹，但在某些情況下，也可以與線性模型一起使用，重要的是要記住每種模型的優點和局限性，并為手頭的問題選擇合適的方法。

1.4 機器學習算法概述

下圖提供了三類機器學習算法的摘要，本文后續部分將更深入研究每個類別。

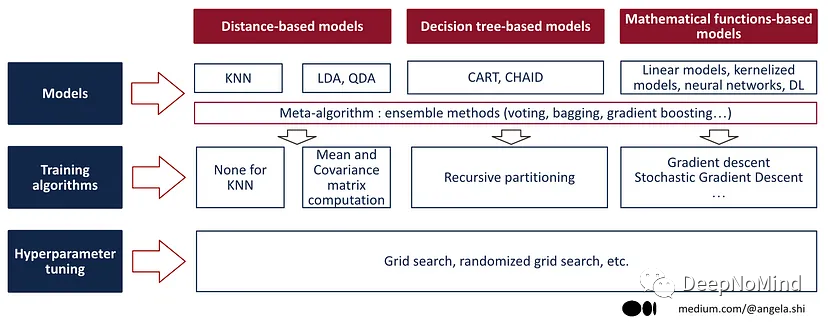
機器學習算法概述

2. 機器學習模型

本節我們將仔細研究機器學習模型的三大類別：

(1) 基于距離的模型

基于距離的模型：KNN

貝葉斯分類：LDA, QDA

(2) 決策樹模型

(3) 基于數學函數的模型

線性模型

核支持向量機(kernel SVM)或核嶺(kernel ridge)等核化模型(Kernelized models)

神經網絡

深度學習模型

2.1 基于距離的模型

第一類機器學習模型是基于距離的模型，這些模型利用數據點之間的距離進行預測。

最簡單、最具代表性的模型是K近鄰模型(KNN, K-Nearest Neighbors)，可以計算新數據點與數據集中所有現有數據點之間的距離，然后選擇K個最近的鄰居，并將新數據點分配給K個鄰居中最常見的類。

在檢驗K近鄰(KNN)算法時，注意到在訓練階段沒有建立顯式模型。在KNN中，對新觀測值的預測是通過在訓練集中找到與該觀測值最近的K個鄰居，并取其目標值的平均值或多數投票來完成的。

與其他算法在訓練期間將模型擬合到數據不同，KNN存儲整個訓練數據集，并簡單地計算新觀測值與現有數據集之間的距離來進行預測。因此，KNN可以被認為是一種"懶學習(lazy learning)"算法，在訓練階段不主動構建模型，并將決策過程推遲到推理時。

因此，推理/測試階段可能很慢，可以用更有效的算法(如k-d樹)進行優化。

2.2 貝葉斯分類

線性判別分析(LDA，Linear Discriminant Analysis)和二次判別分析(QDA，Quadratic Discriminant Analysis)都是基于距離的模型，利用馬氏距離(Mahalanobis distance)進行預測，馬氏距離是點和分布之間距離的度量，因此考慮到了變量之間的相關性。

LDA假設不同類別的方差相同，而QDA假設每個類別的方差不同。這意味著LDA假設所有類別的協方差矩陣是相同的，而QDA允許每個類別有自己的協方差矩陣。

2.3 基于決策樹的模型

第二種機器學習模型是基于決策樹的模型，也被稱為基于規則的模型(rule-based models)。這種模型生成一組規則，用來解釋如何做出決策或預測。

決策樹的每個分支代表一個規則或條件，用于確定接下來要遵循的數據子集。這些規則通常采用簡單的if-then語句的形式，例如"如果變量X的值大于5，則遵循左分支，否則遵循右分支"。

決策樹的最終葉節點表示的是基于輸入變量值以及相關規則所做出的目標變量預測類/值。

決策樹的優點是易于解釋和理解，因為規則可以以清晰直觀的方式可視化和解釋，因此對于向非技術相關方解釋預測或決策背后的原因非常有用。

然而，決策樹也容易出現過擬合，當模型變得過于復雜，與訓練數據擬合過于緊密時，就會出現過擬合，從而導致對新數據的泛化能力差。為了解決這個問題，通常將集成方法應用于決策樹。

2.4 基于數學函數的模型

第三類機器學習模型是基于數學函數的模型，基于數學函數模擬輸入變量和目標變量之間的關系。線性模型(如普通最小二乘(OLS，Ordinary Least Squares)回歸、具有線性核的支持向量機(SVM，Support Vector Machines)、Ridge、LASSO)假設輸入變量與目標變量之間的關系是線性的。非線性模型，如具有非線性核的支持向量機和神經網絡，可以模擬輸入變量和目標變量之間更復雜的關系。

對于基于數學函數的模型，如線性回歸或邏輯回歸，必須定義損失函數。損失函數衡量模型的預測與實際數據的匹配程度，目標是通過調整模型參數最小化損失函數。

相比之下，對于非數學函數為基礎的模型(如KNN或決策樹)，不需要定義損失函數,而是通過不同的方法進行匹配，例如在KNN的情況下找到最近的鄰居，或者在決策樹的情況下根據特征值遞歸分割數據。

在基于數學函數的模型中，定義合適的損失函數至關重要，因為它決定了模型要解決的優化問題。可以根據手頭問題使用不同的損失函數，例如回歸問題的均方誤差或二元分類問題的交叉熵。

值得注意的是，所有具有線性核的線性模型(如OLS、LASSO、Ridge、SVM等)，都可以寫成線性方程y = wX + b的形式。然而，這些模型之間的區別在于用于估計模型參數w和b的最優值的代價函數。

因此，雖然所有這些模型都可以以相同的數學函數的形式編寫，但重要的是要注意選擇的代價函數決定了模型的行為和性能，因此可以將它們視為具有不同代價函數的不同模型，而不是具有不同代價函數的同一模型。

非線性模型是解決復雜機器學習問題的強大工具，而線性模型無法充分解決這些問題。在實踐中基本上有兩種方法：核技巧(kernel trick)和神經網絡。

核技巧是一種有效實現特征映射的方法，無需顯式計算轉換后的特征。相反，它定義核函數來計算轉換后的特征空間中輸入樣本對之間的相似性。通過使用核函數，可以隱式地將輸入數據映射到高維空間，在高維空間中可以更容易地分離和建模。

從這個意義上說，核部分可以看作是特征工程的一種形式，其中模型能夠創建更適合手頭任務的新特征。這與傳統特征工程不一樣，在傳統特征工程中，人類專家根據領域知識和直覺手動創建新特征。

另一種創建非線性模型的方法是使用神經網絡。它們由相互連接的節點或"神經元"層組成，每個節點對其輸入執行簡單的數學運算，并將結果傳遞給下一層。

神經網絡強大的關鍵在于能夠學習輸入和輸出之間復雜的非線性關系。這是通過在訓練期間根據預測輸出和實際輸出之間的誤差調整神經元之間連接的權重來實現的。

2.5 深度學習模型

深度學習的重點是通過多層結構來學習數據的表示。近年來，由于其在計算機視覺、自然語言處理和語音識別等應用中的廣泛成功，變得越來越受歡迎。雖然深度學習模型有大量參數和層，實現相對復雜，但其特征工程也是其重要部分之一。

卷積神經網絡(CNN，convolutional neural network)是深度學習模型的一個例子，其核心是對輸入圖像應用一系列濾波器，每個濾波器尋找特定的特征，如邊緣或角，然后網絡的下一層使用這些提取的特征對輸入圖像進行分類。

像CNN這樣的深度學習模型可以被認為是特征工程和可訓練模型的結合。該模型的特征工程涉及設計網絡架構以從輸入數據中提取有用的特征，而可訓練模型涉及優化網絡參數以擬合數據并做出準確的預測。

3. 模型訓練/擬合

訓練機器學習模型是通過向模型展示一組標記的示例來教模型做出預測或決策的過程。標記的示例，也稱為訓練數據，由成對的輸入特征和輸出標簽組成。

在訓練過程中，機器學習模型學習識別輸入特征及其對應的輸出標簽中的模式。該模型使用特定算法從訓練數據中學習并調整其內部參數，以提高對新數據的預測或分類能力。

一旦模型在標記的例子上進行了訓練，就可以用來對新的、沒見過的數據進行預測或決策，這個過程被稱為推理或測試。

不同的機器學習模型有不同的訓練算法，以下是不同機器學習模型使用的訓練算法的一些示例。

3.1 基于距離的模型訓練

KNN是一種不需要顯式訓練的非參數算法。它存儲整個訓練數據集，并用來預測新實例的標簽，方法是根據一些距離度量在訓練數據集中找到K個最接近的實例，然后根據K個最近鄰居的多數投票進行預測。

LDA是一種用于分類任務的監督學習算法。LDA對每個類的輸入特征的分布進行建模，并用該信息找到輸入特征的線性組合，使類之間的分離最大化。得到的線性判別式可以用來對新實例進行分類。

LDA的訓練過程包括估計每個類別的輸入特征的均值和協方差矩陣，然后用這些估值來計算類內和類間散點矩陣，這些散點矩陣用于導出線性判別式，線性判別式的數量等于類的數量減一。

3.2 基于決策樹的模型訓練

至于決策樹，通常用一種稱為遞歸劃分的方法進行訓練。

遞歸分區從整個數據集開始，自上而下根據一組規則或條件將其分成子集。在每個子集上遞歸重復分割過程，直到滿足停止條件(通常是當子集變得太小或進一步分割無法提高模型性能時)。

分割規則基于數據集特征或屬性，算法在每一步中選擇對模型性能改善最顯著的特征。分割過程產生一個樹狀結構，其中內部節點表示分割條件，葉節點表示最終預測。

在訓練過程中，可以使用各種度量來評估決策樹，例如信息增益或基尼雜質(Gini impurity)，以確定最佳分割標準。一旦訓練好決策樹，就可以根據輸入特征從根節點找到適當的葉節點路徑，對新的、未知的數據進行預測。

3.3 基于數學函數的模型訓練

基于數學函數的模型，也稱為參數模型，是為輸入和輸出之間的關系假設特定函數形式的模型。

用于優化基于數學函數的模型參數的最基本算法是梯度下降(gradient descent)。梯度下降是一種迭代優化算法，它首先對參數值進行初始猜測，然后根據損失函數相對于參數的梯度對參數值進行更新，持續這一過程直到算法收斂到損失函數最小為止。

對于非凸函數(non-convex functions)，通常用隨機梯度下降(SGD, stochastic gradient descent)來代替梯度下降，SGD在每次迭代時隨機抽取一個數據子集來計算梯度，這種方法比梯度下降算法更快、更有效。

在神經網絡中，反向傳播(backpropagation)用于計算損失函數相對于參數的梯度。反向傳播本質上就是將微積分的鏈式法則應用于由神經網絡表示的復合函數，可以有效計算網絡每層的梯度，對于訓練深度神經網絡必不可少。

對于深度學習模型，通常使用更高級的優化技術來提高性能，包括動量(momentum)和自適應學習率(adaptive learning rate)等技術，動量可以幫助算法避免陷入局部最小值，自適應學習率可以在訓練過程中自動調整學習率，以提高收斂速度和穩定性。

綜上所述，梯度下降是優化函數模型參數的基本算法。對于非凸函數，通常使用隨機梯度下降法。反向傳播用于計算神經網絡中的梯度，此外還有其他更高級的技術用于深度學習模型。

4. 模型優化

機器學習的第三個方面包括通過使用網格搜索來優化模型的超參數(hyperparameters)。超參數是模型的設置或配置，這些設置或配置不是在訓練過程中學習到的，而必須手動指定。

超參數的例子包括學習率、神經網絡中隱藏層的數量以及正則化強度等，通過使用網格搜索，評估多個超參數組合，從而可以確定模型的最佳配置。

網格搜索是一種用于優化機器學習模型超參數的常用技術。然而，這并不是唯一可用的方法，還有其他幾種可用于微調模型參數的替代方法，一些最流行的替代方案包括：

隨機網格搜索：與網格搜索相比，隨機搜索涉及從預定義范圍內隨機采樣超參數，從而更有效的探索參數空間。

貝葉斯優化：貝葉斯優化利用概率模型，通過迭代評估模型性能，更新超參數的概率分布，找到超參數的最優集合。

遺傳算法：遺傳算法模擬自然選擇過程，通過產生一組潛在的解決方案，評估其性能，并選擇最適合的個體進行繁殖，從而找到最優的超參數集。

基于梯度的優化：基于梯度的優化涉及使用梯度迭代調整超參數，目的是最大化模型性能。

基于集成的優化：基于集成的優化涉及將具有不同超參數的多個模型組合在一起，以創建更具魯棒性和更準確的最終模型。

每種替代方法都有其優缺點，需要根據所處理的特定問題、參數空間大小和可用計算資源選擇最佳方法。

5. 高效學習機器學習的幾個技巧

現在我們對機器學習算法的不同類別有了大致了解，接下來探索一下為了創建有效的預測模型，需要學習什么。

5.1 算法太難學？

如果我們從一些乍一看可能很復雜的算法開始，就會覺得機器學習是個具有挑戰性的領域。然而，通過將該過程分解為三個階段(建模、擬合和調優)，就能夠獲得更清晰的理解。

例如，學習支持向量機(SVM)對于數據科學家來說可能令人生畏，因為有大量的技術術語，如最優超平面(optimal hyperplane)、無約束最小化(unconstrained minimization)、對偶性(原始和對偶形式)、拉格朗日乘子(Lagrange multipliers)、Karush-Kuhn-Tucker條件、二次規劃等等。然而，有必要將SVM只是理解為一個線性模型，和OLS回歸類似，方程為y = wX + b。

雖然上面提到的各種技術可以被用來優化SVM，但重要的是不要陷入技術問題的泥潭，而是要關注SVM作為線性模型的基本概念。

5.2 了解模型

我們已經討論了三種類型的機器學習算法——模型、擬合算法和調優算法。在我看來，對于數據科學家來說，重要的是將理解模型置于其他兩個步驟之上。

從這個角度來看，將機器學習模型分為三種主要類型，從而有助于理解其功能：

基于距離的模型：在這種類型中，KNN不是一個合適的模型，因為新數據的距離是直接計算的，而在LDA或QDA中，是基于分布距離計算。

基于決策樹的模型：決策樹遵循if-else規則，形成一組可用于決策的規則。

基于數學函數的模型：可能不太容易理解，然而函數通常都很簡單。

一旦對模型如何工作有了堅實的理解，就可以使用預先存在的包來進行擬合和調優:對于擬合，流行的scikit-learn庫提供了model.fit方法。而對于調優，像Optuna這樣的工具通過study.optimize提供了高效的學習優化技術。通過專注于理解模型本身，數據科學家可以更好地為自己在該領域的成功做好準備。

對于一些獨立模型，如果采用這種方法，可以提升對其的理解，這里有一些例子：

多項式回歸是對特征進行不同次冪變換后的線性回歸。

線性回歸、ridge、LASSO和SVR是相同的模型，只是底層代價函數不同。

線性回歸、邏輯回歸和支持向量機是同一模型，只是底層代價函數不同。你可能會注意到線性回歸是回歸量而邏輯回歸和支持向量機是分類器，請閱讀SGDClassifier的文檔或查看關于SGDClassifier的這篇文章[2]。

10個最常見但最令人困惑的機器學習模型名稱說明[3]這篇文章說明理解模型并不總是直截了當的。

5.3 模型可視化

在理解模型時，可視化是一個非常有用的工具。當使用機器學習模型時，使用簡單的數據集創建可視化可以幫助說明模型是如何創建以及如何工作的。

下面一些文章涵蓋的主題包括線性回歸的可視化，也可以應用于ridge、lasso、SVM以及神經網絡。

另一種方法是在Excel中實現模型，因為它可以提供一種可視化的方式來查看數據和模型的輸出。

Visualization of linear regression[4]

Visualization of neural networks[5]

Visualization of Decision Tree Regressors[6]

Nearest Neighbors Regressors — A Visual Guide[7]

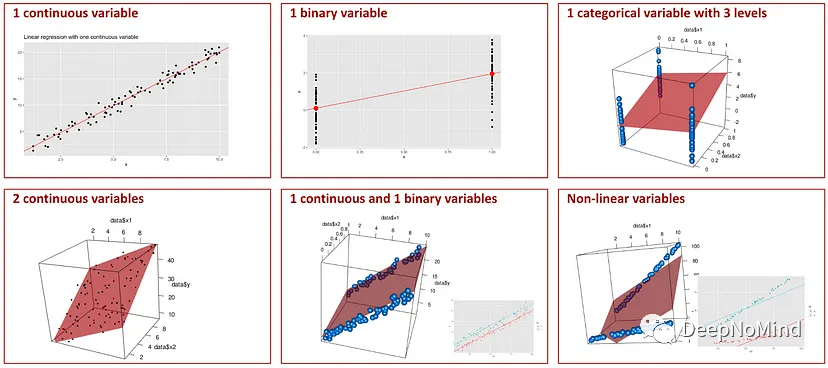
線性回歸的可視化

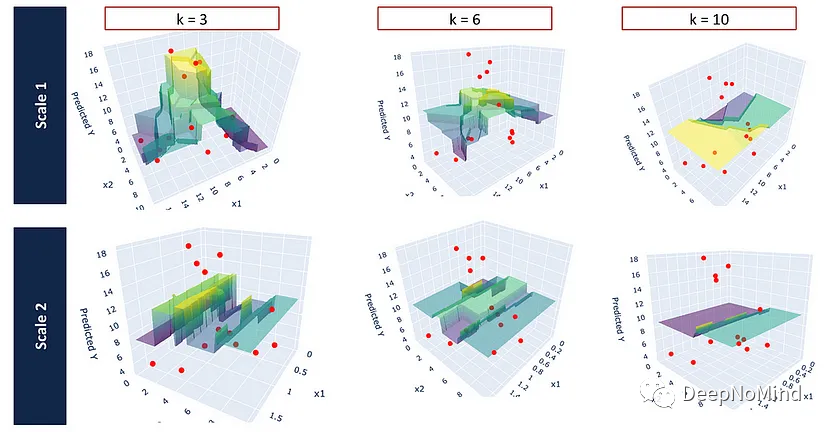
不同特征尺度的KNN回歸器

5.4 使用Excel了解擬合過程

一開始，了解擬合過程可能會讓人望而生畏。但是，如果想要學習，那么首先要對模型的工作原理有一個堅實的理解。在這方面，一個特別有用的工具是微軟Excel。

Excel是一個廣泛使用的電子表格程序，可用于可視化和操作數據。在機器學習領域，可以用來演示擬合過程是如何工作的簡單模型(如線性回歸)。通過使用Excel，可以看到這個算法是如何一步步實現的。

要記住，雖然Excel可以是一種理解簡單數據集的擬合過程的有效方法，但并不是機器學習最有效工具。

用Excel來理解擬合過程對于機器學習初學者來說是一個有用的工具，它提供了一種簡單易用的方法來可視化算法并了解它們是如何工作的。

下面是幾篇關于線性回歸、邏輯回歸和神經網絡梯度下降的文章。

K-Nearest neighbors in Excel[8]

Linear Regression With Gradient Descent in Excel[9]

Logistic Regression With Gradient Descent in Excel[10]

Neural Network Classifier from Scratch in Excel[11]

Decision Tree Regressors in Excel[12]

Implementing KNN in Excel[13]

K-means from Scratch in Excel[14]

Neural Network with Backpropagation in Excel[15]

基于Excel的機器學習算法

5.5 使用簡單數據集進行測試

為了全面理解機器學習算法，從頭開始實現可能是一種有效方法，然而這種方法可能相當耗時，并且可能需要高水平的技術熟練度。另一種方法是使用預先訓練好的包或庫來使用簡單的數據集創建和可視化模型的輸出。

通過這些包，可以輕松試驗不同參數并測試各種機器學習算法。這種方法可以幫助我們了解算法的內部工作原理，同時也使我們能夠快速評估在特定數據集上的有效性。

通過使用這樣的數據集，可以很容易可視化模型的輸入和輸出。反過來，也可以讓我們更深入了解模型是如何進行預測的。此外，通過改變模型的超參數和其他方面，還可以可視化這些變化對模型預測的影響。

這種方法可以幫助初學者開始機器學習，并更好地理解不同算法的工作原理。這是一種獲得實踐經驗和試驗不同模型的極好方法，而無需在實現上花費太多時間。

6. 結論

總之，機器學習是一個復雜的領域。然而，了解三種主要類型的機器學習算法(模型、擬合算法和調優算法)，并根據它們的目標和復雜性進行分類，可以幫助我們全面了解其工作原理。通過優先理解模型，將它們可視化，并在Excel等工具中實現，可以揭開擬合和調優過程的神秘面紗。

審核編輯 ：李倩