麥克斯韋方程,是所有電磁理論的基礎,其微分形式如下圖所示。
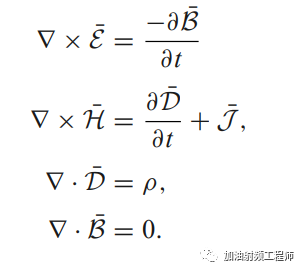
都說麥克斯韋方程是世界上最美的公式之一,可是這幾個方程,到底能讓我們了解些什么呢?
在說這個問題之前,先來說說相量的概念。
歐拉公式告訴我們:
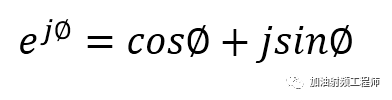
所以對于平面上的任一點Z,可以表示為:
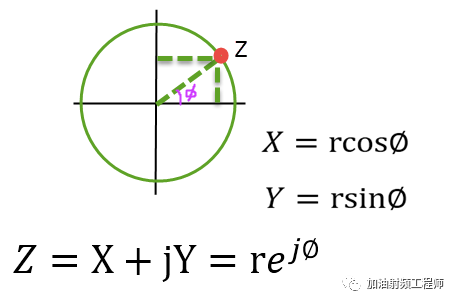
所以,對于一個實正弦信號,可以用下列形式表示:
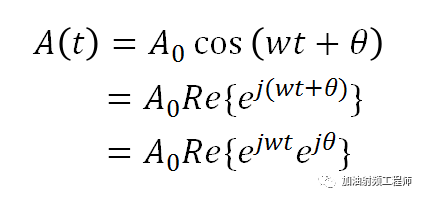
所謂使用相量表示,即:
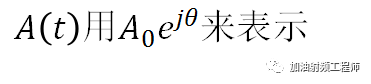
但是,也不是什么時候,都可以用相量進行表示。
從上面公式可知,A(t)的相量形式,省去了Re{}以及e(jwt)。
那什么時候,這兩個可以省去呢?
一種情況是,大家都知道了,寫與不寫,大家都默認是有這兩項的。
也就是說,使用相量形式的前提,是:
(1) 被表示的變量是一個實數,所以不需要將Re{}寫出來
(2) 處理的系統是線性時不變系統,即變量的頻率分量是不變的,因此,不需要把e(jwt)寫出來。
所以,用相量來表示一個正弦信號時,只要寫出其幅度和相位就可以了。
不過,雖然不用寫出來,但是需要記住的是,其實這兩項是存在的。如果對A(t)進行求導的話,不能忘記還有時間的存在,即:
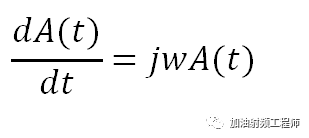
現在,用相量來對麥克斯韋方程中的第一個和第二個旋度方程進行處理。
為了簡化分析,假設所分析區域中的電流和電荷都為0。
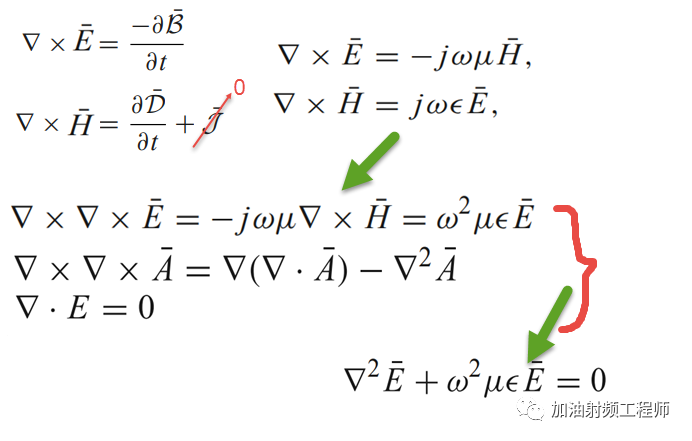
類似的推導,也可以得到:
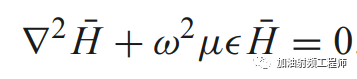
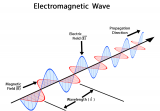
而這兩個式子,就是電磁場的波動方程,或者說是波動方程的相量形式。
波動方程是一個微分方程,這個微分方程,可將變量在時間上的二階導數與其在空間上的二階導數聯系起來。
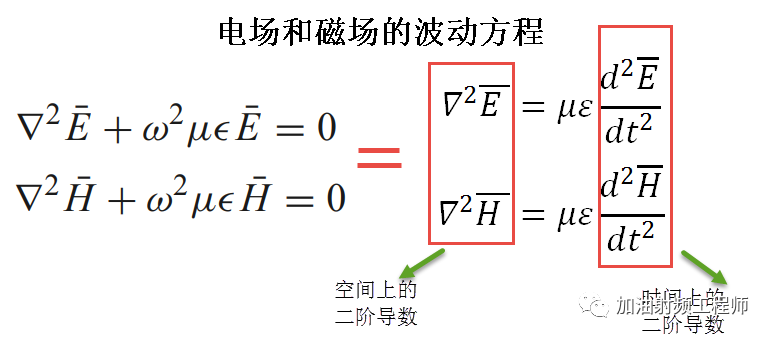
定義波數:

在無耗的媒介中,介電常數和磁導率都為實數,因此k也為實數。
假設電場只存在于x方向,且只隨z的變化而變化。
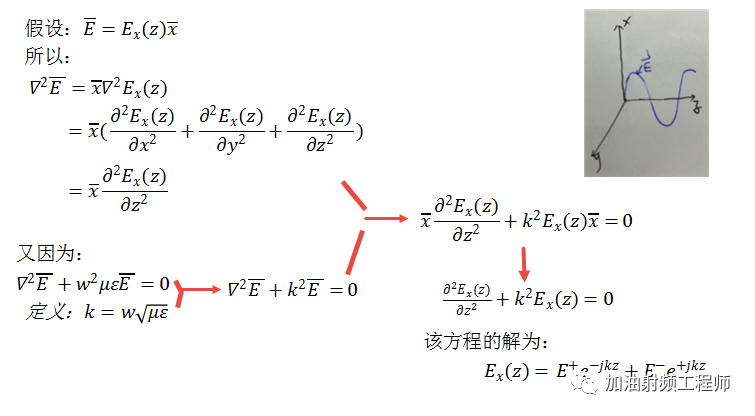
把上面的相量形式改成正常形式后,則:
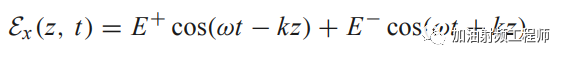
上面式子中的第一項,表示前向波,即隨著時間的增加,波沿著+z軸傳播;而第二項,表示后向波,即隨著時間的增加,波沿著-z軸傳播。
此時,相速,即波的相位在空間中傳播的速度如下式所示:
而電磁波的波長,則定義為在固定的時間點,兩個波峰或者波谷的距離。即:
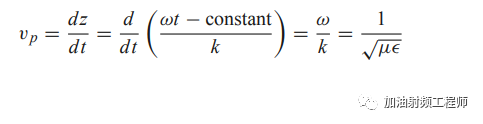
因此,由麥克斯韋方程,可以得到電磁場的波動方程,對波動方程進行求解,即可以得到電場和磁場在時間和空間上的傳播形式。
審核編輯:劉清
-
電磁場
+關注
關注
0文章
797瀏覽量
47859 -
正弦信號
+關注
關注
0文章
46瀏覽量
16862 -
麥克斯韋
+關注
關注
0文章
19瀏覽量
5813
原文標題:麥克斯韋方程是怎么告訴我們波的形式的
文章出處:【微信號:加油射頻工程師,微信公眾號:加油射頻工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
麥克斯韋方程組究竟帶來了什么
麥克斯韋Maxwell方程組是怎么來的
淺析麥克斯韋方程組
電磁場理論之麥克斯韋方程組論文的詳細資料免費下載
追逐麥克斯韋方程組與電磁波理論
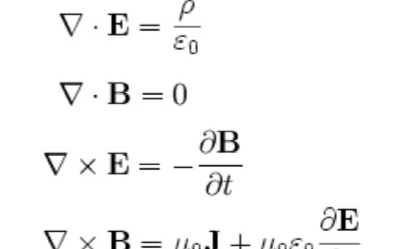
麥克斯韋方程組的詳細資料說明

電磁波的傳播原理和麥克斯韋方程組的詳細說明
射頻微波設計入門——麥克斯韋方程組
描述電磁場的麥克斯韋方程組
麥克斯韋理論:赫茲的電磁波實驗
深度解析麥克斯韋方程
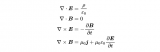


















評論