k-d樹是一種常用的多維數(shù)據(jù)結(jié)構(gòu)，它可以用于范圍搜索、最近鄰搜索等問題。但是，在實(shí)際應(yīng)用中，我們經(jīng)常需要對動態(tài)數(shù)據(jù)進(jìn)行查詢和修改操作。這時候，傳統(tǒng)的k-d樹就顯得力不從心了。為了解決這個問題，研究人員提出了動態(tài)k-d樹（Dynamic k-d Tree）這一概念。與傳統(tǒng)的k-d樹不同，動態(tài)k-d樹可以支持插入、刪除和修改操作，并且能夠保持平衡狀態(tài)。動態(tài)k-d樹可以用于各種多維數(shù)據(jù)結(jié)構(gòu)問題，例如范圍搜索、最近鄰搜索等。本文將介紹動態(tài)k-d樹的基本原理、實(shí)現(xiàn)方法。

1 基本原理

1.1 k-d樹

首先，我們來回顧一下傳統(tǒng)的k-d樹。k-d樹是一種二叉搜索樹，它將每個節(jié)點(diǎn)表示為一個超矩形，并按照某種規(guī)則將超矩形劃分成兩個子區(qū)域。具體來說，k-d樹的構(gòu)建過程如下：

選擇一個維度d，將數(shù)據(jù)集按照第d個維度的值進(jìn)行排序。

選擇中位數(shù)作為根節(jié)點(diǎn)，并將數(shù)據(jù)集分成兩個子集。左子集包含小于中位數(shù)的所有數(shù)據(jù)，右子集包含大于中位數(shù)的所有數(shù)據(jù)。

對左右子集遞歸執(zhí)行步驟1和步驟2，直到每個節(jié)點(diǎn)只包含一個數(shù)據(jù)點(diǎn)

在k-d樹中，每個節(jié)點(diǎn)都表示一個超矩形，其中包含了一些數(shù)據(jù)點(diǎn)。對于任意一個節(jié)點(diǎn)，它的左子樹和右子樹所代表的超矩形是不相交的。因此，在搜索時，我們可以通過比較查詢點(diǎn)與當(dāng)前節(jié)點(diǎn)所代表的超矩形的位置關(guān)系來確定搜索方向。例如，在二維平面上構(gòu)建k-d樹時，每個節(jié)點(diǎn)都代表一個矩形區(qū)域。如果查詢點(diǎn)在當(dāng)前節(jié)點(diǎn)所代表的矩形區(qū)域的左下角，則搜索方向?yàn)樽笞訕洌蝗绻樵凕c(diǎn)在右上角，則搜索方向?yàn)橛易訕洹?/p>

1.2 動態(tài)k-d樹

傳統(tǒng)的k-d樹只能處理靜態(tài)數(shù)據(jù)集，即數(shù)據(jù)集不會發(fā)生變化。但是，在實(shí)際應(yīng)用中，我們經(jīng)常需要對動態(tài)數(shù)據(jù)進(jìn)行查詢和修改操作。例如，在機(jī)器人運(yùn)動規(guī)劃中，機(jī)器人需要不斷地獲取周圍環(huán)境信息，并進(jìn)行路徑規(guī)劃。這時候，傳統(tǒng)的k-d樹就無法滿足需求了。

為了解決這個問題，研究人員提出了動態(tài)k-d樹（Dynamic k-d Tree）這一概念。與傳統(tǒng)的k-d樹不同，動態(tài)k-d樹可以支持插入、刪除和修改操作，并且能夠保持平衡狀態(tài)。

在動態(tài)k-d樹中，每個節(jié)點(diǎn)都代表一個超矩形區(qū)域，其中包含了一些數(shù)據(jù)點(diǎn)。與傳統(tǒng)的k-d樹不同的是，動態(tài)k-d樹中的節(jié)點(diǎn)可以被插入、刪除或修改。當(dāng)一個節(jié)點(diǎn)被插入時，我們需要重新構(gòu)建整個樹；當(dāng)一個節(jié)點(diǎn)被刪除時，我們需要將其從樹中移除，并重新平衡整個樹；當(dāng)一個節(jié)點(diǎn)被修改時，我們需要更新其所代表的超矩形區(qū)域，并重新平衡整個樹。

2. ikd-Tree設(shè)計(jì)與實(shí)現(xiàn)

ikd-Tree是一種基于K-D樹的動態(tài)數(shù)據(jù)結(jié)構(gòu)。它由一個二叉搜索樹組成，在每個節(jié)點(diǎn)上存儲一個超矩形區(qū)域和一個點(diǎn)集合。超矩形區(qū)域是由該節(jié)點(diǎn)所代表的所有點(diǎn)確定的最小超矩形區(qū)域。每個節(jié)點(diǎn)都有一個劃分軸和劃分值來將其子節(jié)點(diǎn)分成兩個子集。ikd-Tree的基本結(jié)構(gòu)，包括節(jié)點(diǎn)、分割平面和子樹等和一些增量操作，包括插入、重新插入和刪除等。在這些操作中，ikd-Tree使用遞歸算法來更新節(jié)點(diǎn)，并通過旋轉(zhuǎn)和重建子樹來保持平衡。此外，該節(jié)還介紹了如何進(jìn)行動態(tài)重新平衡，以避免樹的不平衡導(dǎo)致查詢效率下降。最后，該節(jié)討論了如何使用ikd-Tree進(jìn)行最近點(diǎn)搜索。ikd-Tree 中樹節(jié)點(diǎn)的屬性在下表中給出。第 2-4 行是標(biāo)準(zhǔn) k-d 樹的公共屬性。屬性 left tson 和 rightson 分別是指向它的左子節(jié)點(diǎn)和右子節(jié)點(diǎn)的指針。點(diǎn)信息（例如點(diǎn)坐標(biāo)、強(qiáng)度）存儲在點(diǎn)中。由于一個點(diǎn)對應(yīng)于 k-d 樹上的單個節(jié)點(diǎn)，因此我們將互換使用點(diǎn)和節(jié)點(diǎn)。劃分軸記錄在axis中。第 5-7 行是為第 III-C 節(jié)中詳述的增量更新而設(shè)計(jì)的新屬性。

2.1 增量更新和重新平衡

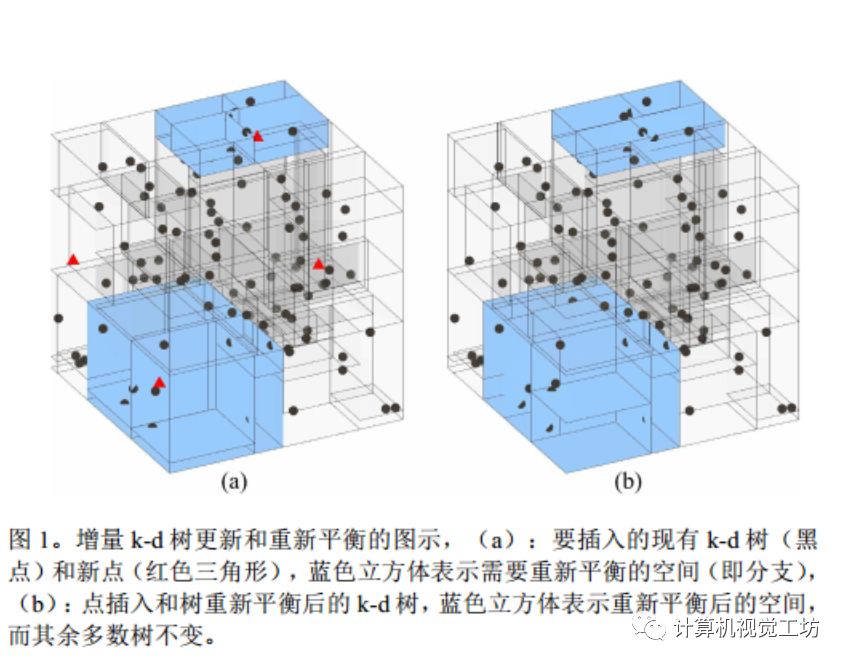
圖1展示了增量k-d樹的更新和重新平衡過程。在這個例子中，黑色點(diǎn)表示現(xiàn)有的k-d樹節(jié)點(diǎn)，紅色三角形表示要插入的新點(diǎn)。藍(lán)色立方體表示需要重新平衡的空間（即分支）。在插入新點(diǎn)后，ikd-Tree使用旋轉(zhuǎn)和重建子樹來保持平衡，并將藍(lán)色立方體移動到正確的位置。

2.2 盒式操作和下采樣

盒式操作是指將空間劃分為多個盒子，以便更快地搜索最近的點(diǎn)。在ikd-Tree中，這是一種針對數(shù)據(jù)坐標(biāo)軸對齊的矩形框內(nèi)的所有點(diǎn)進(jìn)行插入、刪除或重新插入操作的方法。這些矩形框可以由用戶指定，也可以根據(jù)數(shù)據(jù)集自動計(jì)算得出。下采樣是指在保持?jǐn)?shù)據(jù)分布的同時減少數(shù)據(jù)量，從而提高查詢效率。

2.3 動態(tài)重新平衡

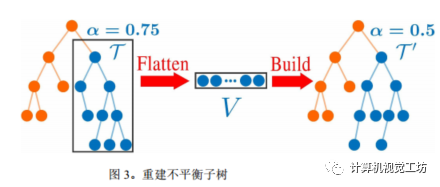
ikd-Tree還支持動態(tài)重新平衡，以避免樹的不平衡導(dǎo)致查詢效率下降。具體來說，ikd-Tree使用部分重建方法來重新平衡樹。當(dāng)需要重新平衡時，ikd-Tree將樹分成兩個部分，并在兩個線程中同時進(jìn)行重建操作。這種方法可以最大限度地減少重建時間，并提高整體效率。

3 時間和空間復(fù)雜度

該節(jié)介紹了ikd-Tree分別對插入、刪除、查詢和重建等操作的時間復(fù)雜度進(jìn)行了分析。最后，該節(jié)還討論了ikd-Tree的空間復(fù)雜度和實(shí)際應(yīng)用中的性能表現(xiàn)。ikd-Tree是一種基于k-d樹的增量數(shù)據(jù)結(jié)構(gòu)，可以在機(jī)器人應(yīng)用中高效地進(jìn)行點(diǎn)云數(shù)據(jù)處理、路徑規(guī)劃等操作。

在ikd-Tree中，每個節(jié)點(diǎn)都包含一個分割平面和兩個子樹，其中左子樹包含小于分割平面值的點(diǎn)，右子樹包含大于等于分割平面值的點(diǎn)。通過遞歸算法，在每個節(jié)點(diǎn)上進(jìn)行二分查找，并通過旋轉(zhuǎn)和重建子樹來保持平衡。在插入操作方面，該節(jié)指出，在最壞情況下，插入一個新點(diǎn)需要O(n)次比較操作（其中n表示樹中節(jié)點(diǎn)數(shù)目）。這是因?yàn)樾曼c(diǎn)可能會被插入到所有節(jié)點(diǎn)的左或右子樹中。但是，在實(shí)際應(yīng)用中，由于ikd-Tree使用動態(tài)重新平衡方法來保持平衡，并且支持下采樣等功能來減少數(shù)據(jù)量，因此插入操作的時間復(fù)雜度通常為O(log n)。

在刪除操作方面，該節(jié)指出，刪除一個節(jié)點(diǎn)需要O(log n)次比較操作。這是因?yàn)閕kd-Tree使用遞歸算法來查找要刪除的節(jié)點(diǎn)，并通過旋轉(zhuǎn)和重建子樹來保持平衡。但是，在實(shí)際應(yīng)用中，由于ikd-Tree支持下采樣等功能來減少數(shù)據(jù)量，因此刪除操作的時間復(fù)雜度通常為O(log n) 在查詢操作方面，該節(jié)指出，ikd-Tree的查詢操作需要O(log n)次比較操作。這是因?yàn)樵诿總€節(jié)點(diǎn)上進(jìn)行二分查找，并根據(jù)分割平面的值來選擇左或右子樹進(jìn)行遞歸查找。由于ikd-Tree使用動態(tài)重新平衡方法來保持平衡，并且支持下采樣等功能來減少數(shù)據(jù)量，因此查詢操作的時間復(fù)雜度通常為O(log n)。

在重建操作方面，該節(jié)指出，ikd-Tree使用部分重建方法來重新平衡樹。當(dāng)需要重新平衡時，ikd-Tree將樹分成兩個部分，并在兩個線程中同時進(jìn)行重建操作。這種方法可以最大限度地減少重建時間，并提高整體效率。由于ikd-Tree支持動態(tài)重新平衡和部分重建等功能，因此重建操作的時間復(fù)雜度通常為O(log n)。

在空間復(fù)雜度方面，該節(jié)指出，ikd-Tree需要O(n)的空間來存儲所有節(jié)點(diǎn)和數(shù)據(jù)點(diǎn)。每個節(jié)點(diǎn)都需要存儲其分割平面、子樹信息以及其他元數(shù)據(jù)。但是，在實(shí)際應(yīng)用中，由于ikd-Tree支持下采樣等功能來減少數(shù)據(jù)量，并且可以通過壓縮存儲等技術(shù)進(jìn)一步減少所需存儲空間。

歡迎關(guān)注「3D視覺工坊」，加群/文章投稿/課程主講，請加微信：dddvisiona，添加時請備注：加群/投稿/主講申請

實(shí)驗(yàn)結(jié)果與分析

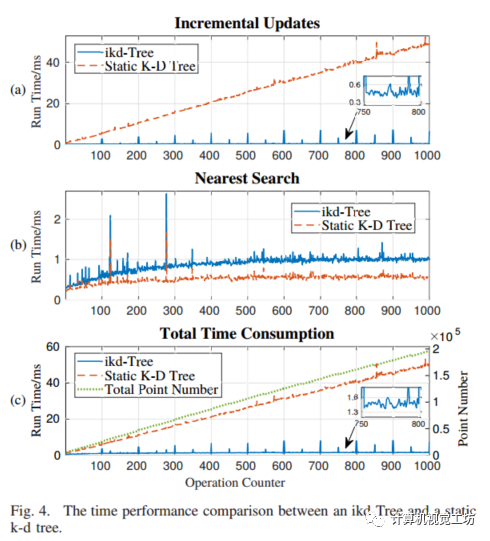
該節(jié)首先介紹了測試環(huán)境和數(shù)據(jù)集，包括使用的硬件和軟件配置以及測試數(shù)據(jù)的來源和特點(diǎn)。然后，該節(jié)詳細(xì)討論了ikd-Tree在不同應(yīng)用場景下的性能表現(xiàn)，并與其他數(shù)據(jù)結(jié)構(gòu)進(jìn)行了比較。這些實(shí)驗(yàn)分別是基于隨機(jī)增量數(shù)據(jù)集的實(shí)驗(yàn)和基于LiDAR測距儀的室外SLAM實(shí)驗(yàn)。在隨機(jī)增量數(shù)據(jù)集實(shí)驗(yàn)中，ikd-Tree的效率得到了充分驗(yàn)證。該實(shí)驗(yàn)使用1000個點(diǎn)作為初始數(shù)據(jù)集，并逐步增加1000個點(diǎn)進(jìn)行測試。圖4(a)展示了ikd-Tree和靜態(tài)k-d樹之間的運(yùn)行時間比較，其中x軸表示增量更新次數(shù)，y軸表示運(yùn)行時間（單位：毫秒）。

可以看出，在增量更新次數(shù)較少時，ikd-Tree和靜態(tài)k-d樹之間的運(yùn)行時間差異不大。但是，當(dāng)增量更新次數(shù)達(dá)到一定數(shù)量時，ikd-Tree明顯優(yōu)于靜態(tài)k-d樹，并且具有更好的擴(kuò)展性。圖4(b)展示了ikd-Tree和靜態(tài)k-d樹之間的最近鄰搜索時間比較，其中x軸表示查詢次數(shù)，y軸表示運(yùn)行時間（單位：毫秒）。可以看出，在查詢次數(shù)較少時，ikd-Tree和靜態(tài)k-d樹之間的查詢時間差異不大。但是，在查詢次數(shù)達(dá)到一定數(shù)量時，ikd-Tree明顯優(yōu)于靜態(tài)k-d樹，并且具有更好的擴(kuò)展性。圖4(c)展示了ikd-Tree和靜態(tài)k-d樹之間的操作計(jì)數(shù)和總時間消耗比較，其中x軸表示點(diǎn)數(shù)，y軸表示操作計(jì)數(shù)和總時間消耗。在點(diǎn)數(shù)達(dá)到一定數(shù)量時，ikd-Tree明顯優(yōu)于靜態(tài)k-d樹。

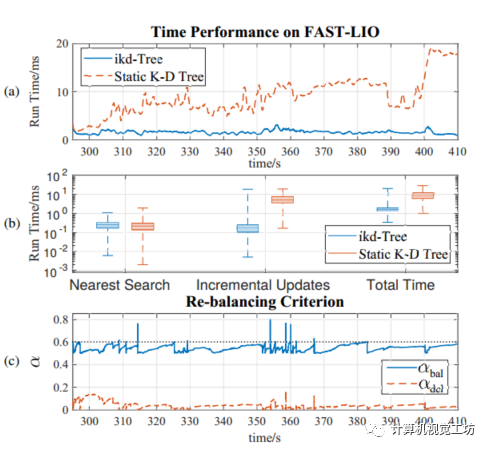
在LiDAR的室外SLAM實(shí)驗(yàn)中，ikd-Tree也表現(xiàn)出了優(yōu)異的性能。該實(shí)驗(yàn)使用了一個移動機(jī)器人和一個LiDAR，通過對周圍環(huán)境進(jìn)行掃描來構(gòu)建地圖。圖5展示了ikd-Tree在該實(shí)驗(yàn)中的性能表現(xiàn)，其中x軸表示時間（單位：秒），y軸表示運(yùn)行時間（單位：毫秒）。可以看出，在整個實(shí)驗(yàn)過程中，ikd-Tree的運(yùn)行時間始終保持在較低水平。

審核編輯：劉清