在使用運算放大器進行電路設計的時候，往往會遇到一個問題，放大之后的波形總是跟理論預期的有差距。這個簡答的運算放大器的問題，涉及到非常多的復雜概念，包括增益誤差，失真度、負反饋、總諧波失真、非線性、開環增益，本文用比較簡潔的語言深入解析下這個疑問。

理解失真度!

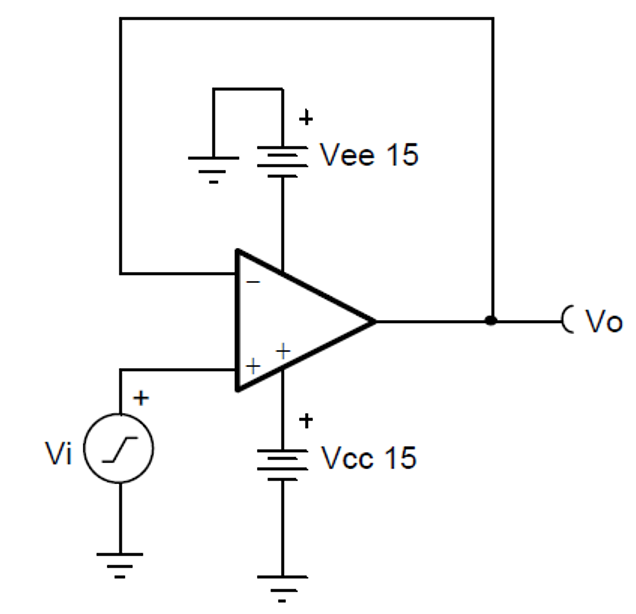
在一個跟隨器電路中(如下圖)，輸入一個正弦波Vi，對于輸出波形Vo是一個跟隨Vi的正弦波，對于Vo和Vi波形從時域上來看，兩者的差異程度即是失真度。但從實際應用的角度，很難去從時域的角度去衡量Vo和Vi兩者的差異程度，所以在頻域上，定義了一種描述正弦信號失真度的參數，稱為總諧波失真(Total Harmonic Distortion, THD)。

總諧波失真(Total Harmonic Distortion)

對時域信號進行傅里葉變換，用如下公式表示THD，其中U1是基波的有效值;得到各次諧波大小，U2表示二次諧波，U3表示三次諧波, …Un表示n次諧波有效值，用UH表示所有諧波的有效值。

失真度用%表示，比如信號發生器發出的正弦波，其THD=0.01%，此外，也可以用dB來表示，THD=20log(THD)dB，對于THD=0.01%的正弦波，其失真度-80dB。

開環增益導致的放大倍數的誤差!

如上圖，是一個同相比例放大電路(Close Loop Gain=2)，根據運算放大器開環增益的定義，Avol=Vout/(Vpos-Vneg)，可以得到：

同時，根據反相端的偏置電流為0，則Vneg的電壓等于Vout在R1和Rf上的分壓產生即：

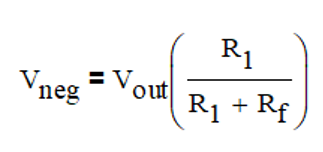
基于上述兩個等式，整理可以得到閉環增益的表達式(如下)，從該表達式可以看到，實際對于同相比例放大電路，其閉環增益會受到開環增益的影響，只有當開環增益無窮大的時候，閉環增益才完全由比例電阻決定，Close Loop Gain=1+Rf/R1。

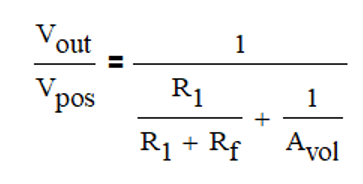
基于此，我們來看看對于實際的運算放大器，開環增益對1kHz的正弦波的放大的影響，下圖是德州儀器OPA2171規格書中開環增益曲線，從圖中讀出在1kHz的時候，開環增益是70dB，即10^3.5=3162，將3162代入上述閉環增益表達式得到閉環增益是1.9987，相比預期的Close Loop Gain=2偏差了0.065%。

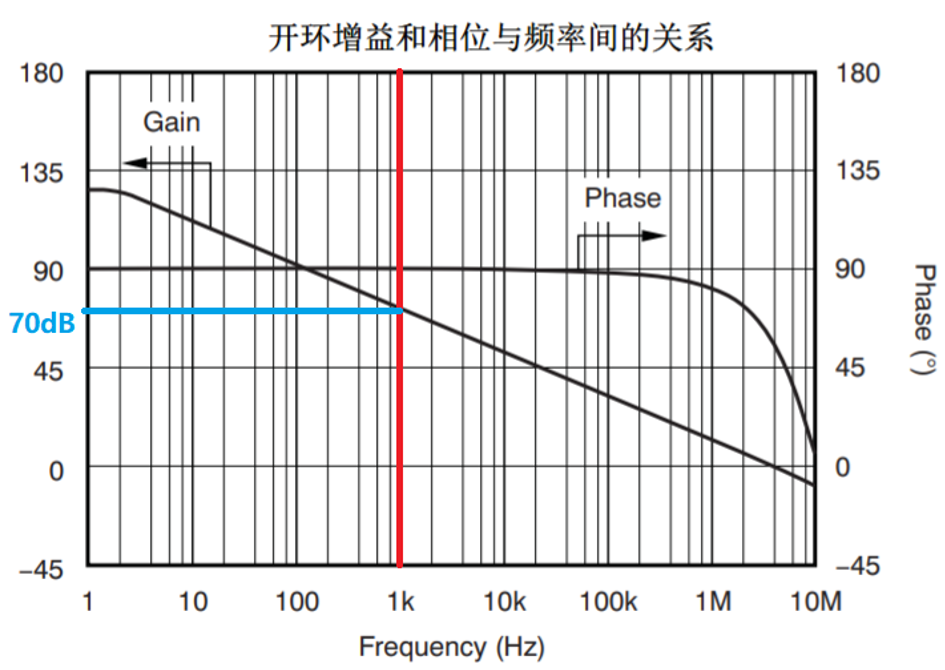
開環增益不是恒定的!

從上述分析，可以看到，如果對于1kHz的標準正弦波下，開環增益是固定的話，其只會帶來閉環增益誤差，這并不會帶來非線性，即對于1kHz的正弦波放大2倍還是1.9987倍，其不會帶來額外的次諧波，這樣THD=0。

但實際上對于運算放大器其開環增益并不是恒定的，運放內部的是由多級晶體管構成，而晶體管的輸入伏安特性曲線是指數型的，這就造成運算放大器的輸入輸出特性曲線是非線性的， 這就使得不同的供電、不同的共模輸入均會導致實際開環增益的變化(通常運算放大器的規格書中標注的開環增益值都是在給定的條件下實測的值)，一旦對于1kHz的標準正弦波，在做2倍放大的時候，因為輸入共模電壓的變化，而導致開環增益一直處于變化中，這就導致放大后的正弦波是存在一定的失真。

但再回到上述對于閉環增益的公式(如下)，同樣對于70dB@1kHz的開環增益，假如其開環增益變化范圍從3000~4000變化，則閉環增益在1.9987~1.999這個區間變化，其閉環增益變化0.015%，實際對1kHz的正弦波的失真度影響非常小，如果我們進一步降低失真度，則可以選擇同等條件下開環增益更大的器件。

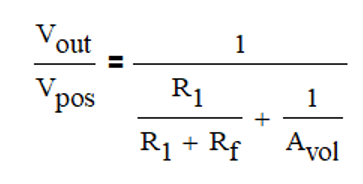
總的來說，如果想要獲得更理想的放大倍數的輸出波形，想要失真度最小的輸出波形，可以選擇同等條件下開環增益更大的器件。