2、多維數組的計算
多維數組:np.dim()可以獲得數組的維數,np.shape()可以獲得數組的形狀,返回一個元組,對應每一個維度的元素個數。二維數組即矩陣。
矩陣乘法:np.dot(A,B)可以求A,B矩陣的乘積(點積),A(m×n)·B(n×k)=C(m×k)
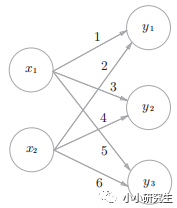
神經網絡的內積:下圖所示的簡單神經網絡,輸入X是一維數組,W是二維數組,Y是一維數組。X(2)·W(2×3)=Y(3)
3、三層神經網絡的實現
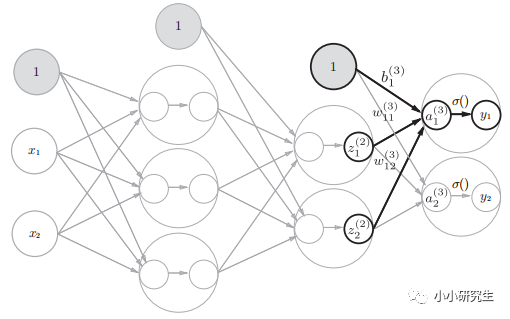
前向傳遞:輸入到輸出的傳遞。需要注意的是目前代碼中的W,B都是人為賦值的。
1'從輸入到第一個隱藏層:
A(1)=XW(1)+B(1)其中A(1)是輸入層中的具有兩個元素的一維數組,W是(2,3)的二維數組,B是具有三個元素的一維數組。用一行代碼即可實現:
A1=np.dot(X,W1)+B1
激活函數選擇sigmoid(),第一個隱藏層中神經元是激活函數轉換后的輸出:
Z1=sigmoid(A1)
2'從第一個隱藏層到第二個隱藏層:
第一個隱藏層的輸出Z1第二個隱藏層的輸入X:A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)
3'第二個隱藏層到輸出層:
A3=np.dot(Z2,W3)+B3
激活函數選用恒等函數y=x,需要自己定義:
def identity_function(x):
return x
Y=identity_function(A3)
4、輸出層的設計
輸出層激活函數,一般回歸問題可以用恒等函數,二元分類問題用sigmoid函數,多元分類問題用softmax函數。分類是區別輸入屬于哪一個類別的問題,回歸是預測一個數值的問題。
已經介紹過恒等和sigoid,現在介紹一下softmax函數。
yk=exp(ak)/∑1nexp(ai)
輸出層有n個神經元,第k個輸出是第k個輸入的指數函數除以每個輸入的指數函數的和,輸出與所有輸入都有關。這個函數需要定義才能使用,注意這個函數用到指數函數,存在溢出的問題,需要對分子分母同除以一個常數,即分子分母的指數同減去一個常數,為了防止溢出,取輸入的最大值:
defsoftmax(a):
C=np.max(a)
exp_a=np.exp(a-C)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return y
softmax函數的特征是輸出0-1之間的實數,且輸出值的總和為1,因此可以把函數的輸出解釋為概率。輸出層神經元的數量就是類別的數量。由于指數函數單調遞增,輸出最大值的即概率最高的分類。一般神經網絡只把輸出值最大的神經元對應的類別作為識別結果。
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100741 -
函數
+關注
關注
3文章
4329瀏覽量
62585 -
神經元
+關注
關注
1文章
363瀏覽量
18450 -
數組
+關注
關注
1文章
417瀏覽量
25941 -
深度學習
+關注
關注
73文章
5503瀏覽量
121125
發布評論請先 登錄
相關推薦




 深度學習基礎知識(3)
深度學習基礎知識(3)












評論