在上一篇介紹奈奎斯特-香農定理的文章中，我們看到當以每個周期不提供至少兩個樣本的頻率對波形進行采樣時，正弦波的頻率特性將無法挽回地丟失。換句話說，如果我們以低于奈奎斯特速率的頻率進行采樣，我們就無法完美地重建正弦曲線。

然而，大多數信號不是單頻正弦波。例如，調制的 RF 信號具有與載波和基帶波形相關聯的頻率，代表人類語音的音頻信號將覆蓋一定范圍的頻率。

我們使用傅立葉變換來可視化信號的頻率內容。時域圖是傳達單頻信號背景下采樣率不足的影響的好方法，但對于其他類型的信號，我寧愿使用頻域。

采樣的頻域效應

假設我們想要數字化一個音頻信號，該信號包括指定范圍內的許多不同頻率的混合。范圍的高端定義為 fMAX，我們假設范圍向下延伸至 DC，即使我們聽不到那么低的頻率。這種信號的傅里葉變換可能看起來像這樣：

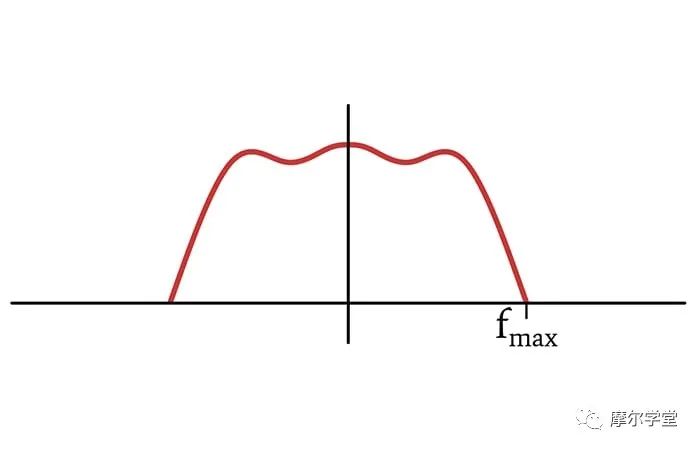
時域中的數學采樣

在數學領域，理想采樣等效于將原始時域波形乘以一系列 delta 函數，間隔等于 1/fSAMPLE，我們稱之為 TSAMPLE。（對于本文的其余部分，我們將使用 fS表示 fSAMPLE并使用 TS表示 TSAMPLE。）這種乘法導致采樣信號在 delta 函數之間為零，并在每個點保留原始信號的值在與 delta 函數重合的時間。

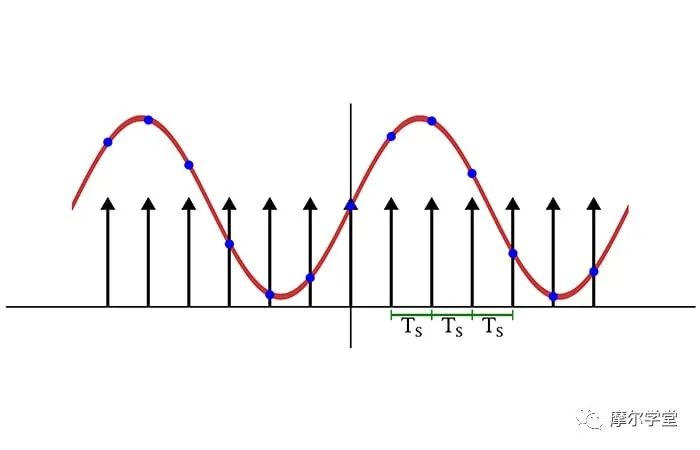
以數學方式實現的時域采樣：我們將模擬信號乘以以采樣頻率出現的一系列 delta 函數。

頻域中的數學采樣

這種時域采樣過程如何影響信號的頻域表示？讓我們來看看。

首先要記住的是，時域中的乘法變成了頻域中的卷積。因此，我們可以通過將原始信號的傅里葉變換與delta函數的傅里葉變換進行卷積來求出采樣信號的傅里葉變換。

事實證明，delta-function train 的 Fourier 變換是 delta-function train。不同之處在于 delta 函數由對應于采樣頻率而不是采樣周期的水平距離分隔。

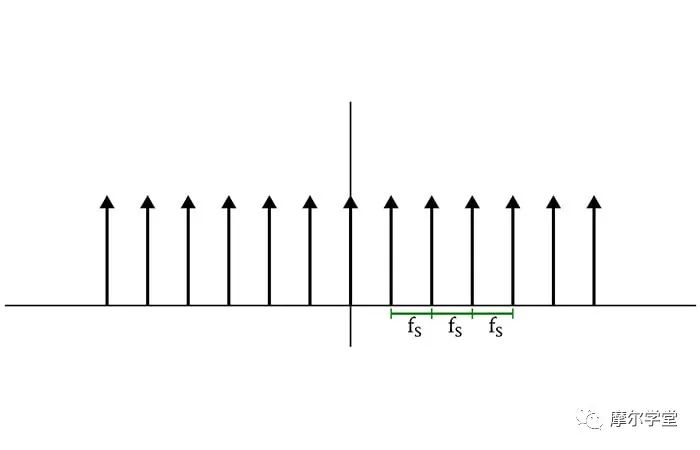
由采樣周期分隔的一系列 delta 函數的頻譜是由采樣頻率分隔的一系列 delta 函數。

當我們將 delta 函數的頻譜與原始信號的頻譜進行卷積時，我們創建了根據 delta 函數的位置移動的原始頻譜的副本。因此，采樣信號的頻譜由多個相同的“子頻譜”組成，這些“子頻譜”以±fS、±2fS、±3fS等為中心。

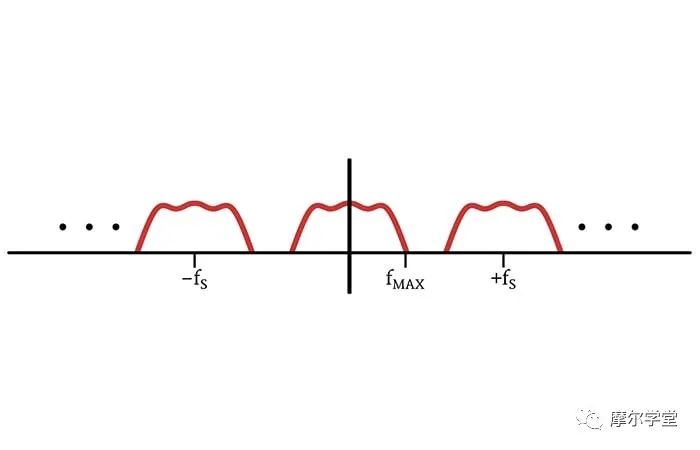
足夠的采樣頻率會導致子光譜發生足夠的偏移以保持完全分離。

我們現在擁有通過頻域分析確認奈奎斯特-香農定理所需的信息。正如我在上一篇文章中表達的那樣，這個定理如下：

如果系統以超過信號最高頻率至少兩倍的速率對模擬信號進行均勻采樣，則可以從采樣產生的離散值中完美地恢復原始模擬信號。

由于傅立葉變換的負頻率部分，原始信號的完整數學帶寬為 2fMAX。因此，為了確保子光譜不重疊，我們必須將它們至少移動 2fMAX。換句話說，采樣頻率必須比信號的最大頻率至少高兩倍。

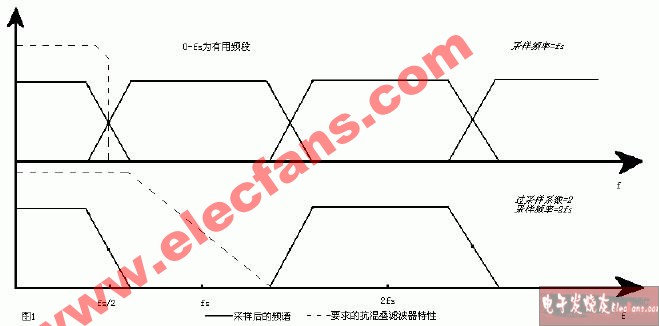
如果滿足這個條件，就可以完美地重建原始信號。為什么？因為原始光譜沒有改變，我們可以通過低通濾波去除其他子光譜。（下一篇文章將更詳細地探討這一點。）如果不滿足條件，則子頻譜重疊，原始頻譜被改變，再多的低通濾波也無法恢復原始信號。

混疊

當我們使用低于奈奎斯特速率的采樣頻率時，子譜重疊是信息被破壞的原因。子譜的重疊部分通過加法合并；如果我們嘗試使用低通濾波器分離出原始頻譜，重疊頻帶中的頻率成分將不同，因此相應的時域信號將不同。

這個的正式名稱是aliasing。

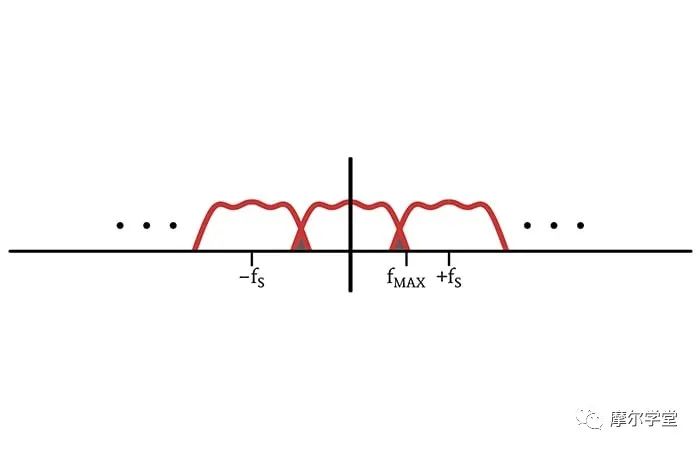
棕色陰影的三角形區域表示導致光譜改變的混疊。

名詞“別名”的定義之一是“虛假或假定的身份”。我們使用術語“混疊”是因為這種采樣現象會導致一個頻率分量移動到頻譜中的一個新位置，從而將其自身“偽裝”為不同的頻率。

我們在上一篇文章中看到了這一點，其中以 1.1f信號采樣導致離散時間波形的頻率似乎遠低于原始模擬波形的頻率。

結論

至此，我認為我們已經涵蓋了抽樣理論的基礎方面。在下一篇文章中，我們將開始在理論和實踐之間建立一些聯系。

彩蛋來了

5月30-31號、6月08-09號，兩期從基礎到高級的ADC講座，將涵蓋高速ADC設計的原理、傳統架構和最先進的設計。第一部分首先回顧了ADC的基本知識，包括采樣、開關電容和量化理論。接下來，介紹了經典ADC架構的基礎和設計實例，如閃存、SAR和流水線ADC。然后，本教程將對混合型ADC架構進行總體概述，這就結束了第一部分。在第二部分，首先描述了ADC的度量。然后，介紹混合或非混合架構的各種先進設計。該教程最后將以數字輔助解決技術結束。

審核編輯：湯梓紅