隨著網格尺寸的增加,雅可比、高斯-賽德爾或 ILU(不完全 LU)等傳統(tǒng)迭代求解算法的收斂速度明顯降低。 反過來,收斂緩慢會導致計算時間呈二次性增加。為加速求解器收斂,采用代數多重網格 (AMG) 法。多重網格法的概念基于以下事實:迭代求解算法可有效減少其波長對應于網格單元尺寸(高頻誤差)的數值誤差分量。 但對于此類方法,長波長(低頻)誤差的降幅相當緩慢。
在連續(xù)粗糙化的線性系統(tǒng)的層次結構上,多重網格法通過迭代過程減少低頻誤差。代數多重網格衍生粗糙層方程組,而不參考基礎網格幾何。粗糙網格方程從精細網格系數的算術組合衍生得出。幾次迭代之后,多重網格算法將計算從精細線性系統(tǒng)傳遞到粗糙線性系統(tǒng)。 這些迭代也稱為平滑迭代,因為誤差函數稍后將會平滑(即不含誤差的高頻分量)。
由于求解過程傳遞到更粗糙的線性系統(tǒng),因此誤差現在相對網格單元尺寸而言頻率增高并可有效減少。 在更粗糙的線性系統(tǒng)上,為減少精細線性系統(tǒng)求解的誤差,定義了缺陷方程。多重網格算法采用以下步驟:
- 聚結網格單元,形成粗糙網格級別。
- 將殘差從精細級別傳遞到更粗糙的級別(稱為限制)。
- 將校正從粗糙級別傳遞回更精細的級別(稱為延長)。
-
多重網格循環(huán)
多重網格方法支持通過在粗糙網格序列上使用簡單校正掃掠,顯著加速高斯-賽德爾等基本迭代格式的運行。粗糙級別訪問策略可能會對該算法的效率產生很大的影響。AMG中有兩個循環(huán)策略,即固定和可變:
-
固定循環(huán)
完整的多重網格循環(huán)表示遞歸應用由以下步驟組成的單一循環(huán):
- a) (預)平滑;
- b) 限制;
- c) 再循環(huán);
- d) 延長;
- e) (后)平滑。
這些步驟將應用于一系列連續(xù)粗糙化的網格或方程組。平滑表示將任意數量的迭代松弛掃掠應用于當前精細級別上的方程,計算一組新校正。限制是指將現有殘差向下傳遞到應用了新循環(huán)的下一個最粗糙級別。隨后,結果校正將延長,即傳遞回同樣應用了平滑的當前精細級別。有以下三種類型的固定循環(huán):
- F 固定循環(huán)
- V 固定循環(huán)
- W 固定循環(huán)
- 可變循環(huán)
對于非剛性線性系統(tǒng),此類循環(huán)是一種更經濟的循環(huán)策略。每次在給定網格級別上掃掠后都會監(jiān)視殘差,而非按規(guī)則模式使用所有多重網格級別。如果殘差減少率超出給定閾值,會繼續(xù)在更粗糙的級別上求解。如果給定級別上的殘差降幅超過指定閾值,則求解將轉到更精細的級別。任何級別允許的掃掠數將進一步受到限制。
V 循環(huán)
V 循環(huán)是最簡單的固定循環(huán)類型,只有兩個分支。 在第一個分支中,用戶對最精細的級別執(zhí)行大量松弛掃掠并將殘差傳遞到下一個級別。 然后,對粗糙級別相繼重復該操作,直至達到最粗糙的級別為止。粗糙“網格”通常僅包含幾個“網格單元”。在最粗糙的級別上完成掃掠之后,使用得到的解校正下一個更精細級別上的求解。先在該級別執(zhí)行一些松弛掃掠,然后重復此過程,直至達到最精細的級別為止,圖 顯示了此過程。
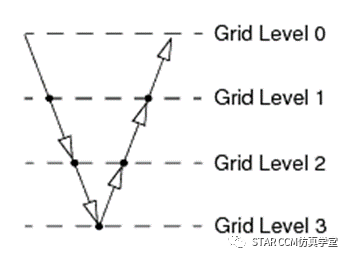
W 循環(huán)
對于剛性方程組,V 循環(huán)有時不能滿足需要,進行更多粗糙迭代非常有用。W循環(huán)會增加粗糙松弛掃掠數,如圖 所示。

F 循環(huán)
F循環(huán)是W循環(huán)的一種變體,此循環(huán)如圖示,涉及的粗糙級別掃掠數少于W循環(huán),但仍多于 V 循環(huán)。

-
CCM
+關注
關注
0文章
165瀏覽量
24810 -
線性系統(tǒng)
+關注
關注
0文章
43瀏覽量
14944 -
求解器
+關注
關注
0文章
82瀏覽量
4765
發(fā)布評論請先 登錄
基于貪婪算法的配電網網格負荷預測與規(guī)劃
網格和密度的聚類算法在CRM中的應用
基于多重網格方法的快速電源網格分析法
網格劃分原理與實例
奇異攝動問題的移動網格算法
多重網格格子Boltzmann方法
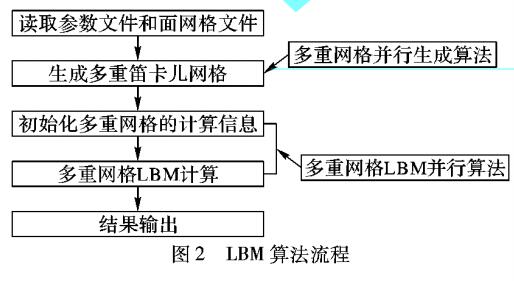
基于數據驅動的任務并行多重網格應用
可提高網格建模的非線性引導濾波算法
Nimbix云提供的技術支持
Simcenter STAR-CCM+流體仿真軟件

【Simcenter STAR-CCM+】通過快速準確的CFD仿真加速空氣動力學創(chuàng)新

【Simcenter STAR-CCM+】通過真實條件下的多物理場CFD仿真提高產品性能




















評論