記得我還在大四的時候，在申請出國和保研中猶豫了好一陣，骨子里的保守最后讓我選擇了先保研。當然后來也退學了，不過這是后話。當時保研就要找老板，實驗室，自己運氣還不錯，進了一個在本校很牛逼的實驗室干活路。我們實驗室主要是搞圖像的，實力在全國也是很強的，進去后和師兄師姐聊，大家都在搞什么小波變換，H264之類的。當時的我心思都不在這方面，盡搞什么操作系統移植，ARM+FPGA這些東西了。對小波變換的認識也就停留在神秘的“圖像視頻壓縮算法之王”上面。

后來我才發現，在別的很廣泛的領域中，小波也逐漸開始流行。比如話說很早以前，我們接觸的信號頻域處理基本都是傅立葉和拉普拉斯的天下。但這些年，小波在信號分析中的逐漸興盛和普及。這讓人不得不感到好奇，是什么特性讓它在圖象壓縮，信號處理這些關鍵應用中更得到信賴呢?說實話，我還在國內的時候，就開始好奇這個問題了，于是放狗搜，放毒搜，找遍了中文講小波變換的科普文章，發現沒幾個講得清楚的，當時好奇心沒那么重，也不是搞這個研究的，懶得找英文大部頭論文了，于是作罷。后來來了這邊，有些項目要用信號處理，不得已接觸到一些小波變換的東西，才開始硬著頭皮看。看了一些材料，聽了一些課，才發現，還是那個老生常談的論調：國外的技術資料和國內真TNND不是一個檔次的。同樣的事情，別人說得很清楚，連我這種并不聰明的人也看得懂; 國內的材料則繞來繞去講得一塌糊涂，除了少數天才沒幾個人能在短時間掌握的。

牢騷就不繼續發揮了。在這個系列文章里，我希望能簡單介紹一下小波變換，它和傅立葉變換的比較，以及它在移動平臺做motiondetection的應用。如果不做特殊說明，均以離散小波為例子。考慮到我以前看中文資料的痛苦程度，我會盡量用簡單，但是直觀的方式去介紹。有些必要的公式是不能少的，但我盡量少用公式，多用圖。另外，我不是一個好的翻譯者，所以對于某些實在翻譯不清楚的術語，我就會直接用英語。我并不claim我會把整個小波變換講清楚，這是不可能的事，我只能盡力去圍繞要點展開，比如小波變換相對傅立葉變換的好處，這些好處的原因是什么，小波變換的幾個根本性質是什么，背后的推導是什么。我希望達到的目的就是一個小波變換的初學者在看完這個系列之后，就能用matlab或者別的工具對信號做小波變換的基本分析并且知道這個分析大概是怎么回事。

最后說明，我不是研究信號處理的專業人士，所以文中必有疏漏或者錯誤，如發現還請不吝賜教。

要講小波變換，我們必須了解傅立葉變換。要了解傅立葉變換，我們先要弄清楚什么是”變換“。很多處理，不管是壓縮也好，濾波也好，圖形處理也好，本質都是變換。變換的是什么東西呢?是基，也就是basis。如果你暫時有些遺忘了basis的定義，那么簡單說，在線性代數里，basis是指空間里一系列線性獨立的向量，而這個空間里的任何其他向量，都可以由這些個向量的線性組合來表示。那basis在變換里面啥用呢?比如說吧，傅立葉展開的本質，就是把一個空間中的信號用該空間的某個basis的線性組合表示出來，要這樣表示的原因，是因為傅立葉變換的本質，是。小波變換自然也不例外的和basis有關了。再比如你用Photoshop去處理圖像，里面的圖像拉伸，反轉，等等一系列操作，都是和basis的改變有關。

既然這些變換都是在搞基，那我們自然就容易想到，這個basis的選取非常重要，因為basis的特點決定了具體的計算過程。一個空間中可能有很多種形式的basis，什么樣的basis比較好，很大程度上取決于這個basis服務于什么應用。比如如果我們希望選取有利于壓縮的話，那么就希望這個basis能用其中很少的向量來最大程度地表示信號，這樣即使把別的向量給砍了，信號也不會損失很多。而如果是圖形處理中常見的線性變換，最省計算量的完美basis就是eigenvector basis了，因為此時變換矩陣T對它們的作用等同于對角矩陣( Tv_n = av_n，a是eigenvalue )。總的來說，拋開具體的應用不談，所有的basis，我們都希望它們有一個共同的特點，那就是，容易計算，用最簡單的方式呈現最多的信號特性。

好，現在我們對變換有了基本的認識，知道他們其實就是在搞基。當然，搞基也是分形式的，不同的變換，搞基的妙處各有不同。接下來先看看，傅立葉變換是在干嘛。

傅立葉級數最早是Joseph Fourier 這個人提出的，他發現，這個basis不僅僅存在與vector space，還存在于function space。這個function space本質上還是一個linear vector space，可以是有限的，可以是無限的，只不過在這個空間里，vector就是function了，而對應的標量就是實數或者復數。在vector space里，你有vector v可以寫成vector basis的線性組合，那在function space里，function f(x)也可以寫成對應function basis的線性組合，也有norm。你的vector basis可以是正交的，我的function basis也可以是正交的(比如sin(t)和sin(2t))。唯一不同的是，我的function basis是無窮盡的，因為我的function space的維度是無窮的。好，具體來說，那就是現在我們有一個函數，f(x)。我們希望將它寫成一些cos函數和一些sin函數的形式，像這樣

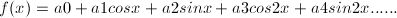
again，這是一個無限循環的函數。其中的1，cosx, sinx, cos2x …..這些，就是傅立葉級數。傅立葉級數應用如此廣泛的主要原因之一，就是它們這幫子function basis是正交的，這就是有趣的地方了。為什么function basis正交如此重要呢?我們說兩個vector正交，那就是他倆的內積為0。那對于function basis呢?function basis怎么求內積呢?

現在先復習一下vector正交的定義。我們說兩個vector v,w如果正交的話，應符合：

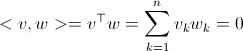
那什么是function正交呢?假設我們有兩個函數f(x)和g(x)，那是什么?我們遵循vector的思路去想，兩個vector求內積，就是把他們相同位置上對應的點的乘積做一個累加。那移過來，就是對每一個x點，對應的f和g做乘積，再累加。不過問題是，f和g都是無限函數阿，x又是一個連續的值。怎么辦呢?向量是離散的，所以累加，函數是連續的，那就是…….積分!

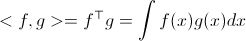
我們知道函數內積是這樣算的了，自然也就容易證明，按照這個形式去寫的傅立葉展開，這些級數確實都是兩兩正交的。證明過程這里就不展開了。好，下一個問題就是，為什么它們是正交basis如此重要呢?這就牽涉到系數的求解了。我們研究了函數f，研究了級數，一堆三角函數和常數1，那系數呢?a0, a1, a2這些系數該怎么確定呢?好，比如我這里準備求a1了。我現在知道什么?信號f(x)是已知的，傅立葉級數是已知的，我們怎么求a1呢?很簡單，把方程兩端的所有部分都求和cosx的內積，即：

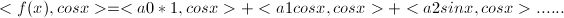
然后我們發現，因為正交的性質，右邊所有非a1項全部消失了，因為他們和cosx的內積都是0!所有就簡化為

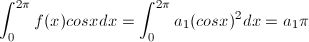
這樣，a1就求解出來了。到這里，你就看出正交的奇妙性了吧:)

好，現在我們知道，傅立葉變換就是用一系列三角波來表示信號方程的展開，這個信號可以是連續的，可以是離散的。傅立葉所用的function basis是專門挑選的，是正交的，是利于計算coefficients的。但千萬別誤解為展開變換所用的basis都是正交的，這完全取決于具體的使用需求，比如泰勒展開的basis就只是簡單的非正交多項式。

有了傅立葉變換的基礎，接下來，我們就看看什么是小波變換。首先來說說什么是小波。所謂波，就是在時間域或者空間域的震蕩方程，比如正弦波，就是一種波。什么是波分析?針對波的分析拉(囧)。并不是說小波分析才屬于波分析，傅立葉分析也是波分析，因為正弦波也是一種波嘛。那什么是小波呢?這個”小“，是針對傅立葉波而言的。傅立葉所用的波是什么?正弦波，這玩意以有著無窮的能量，同樣的幅度在整個無窮大區間里面振蕩，像下面這樣：

那小波是什么呢?是一種能量在時域非常集中的波。它的能量是有限的，而且集中在某一點附近。比如下面這樣：

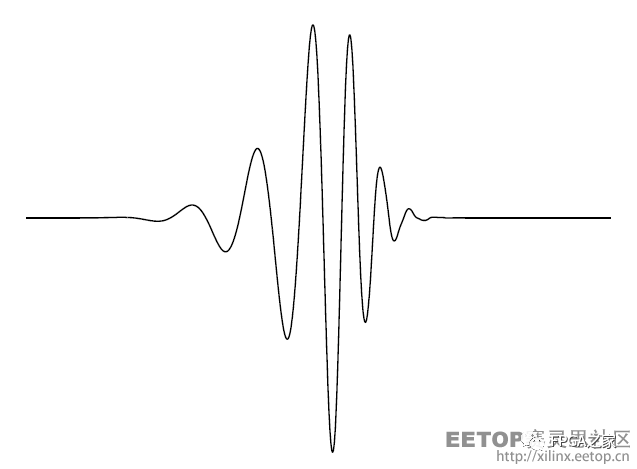
這種小波有什么好處呢?它對于分析瞬時時變信號非常有用。它有效的從信號中提取信息，通過伸縮和平移等運算功能對函數或信號進行多尺度細化分析，解決了傅立葉變換不能解決的許多困難問題。恩，以上就是通常情況下你能在國內網站上搜到的小波變換文章告訴你的。但為什么呢?這是我希望在這個系列文章中講清楚的。不過在這篇文章里，我先點到為止，把小波變換的重要特性以及優點cover了，在下一篇文章中再具體推導這些特性。

小波變換的本質和傅立葉變換類似，也是用精心挑選的basis來表示信號方程。每個小波變換都會有一個mother wavelet，我們稱之為母小波，同時還有一個scaling function，中文是尺度函數，也被成為父小波。任何小波變換的basis函數，其實就是對這個母小波和父小波縮放和平移后的集合。下面這附圖就是某種小波的示意圖：

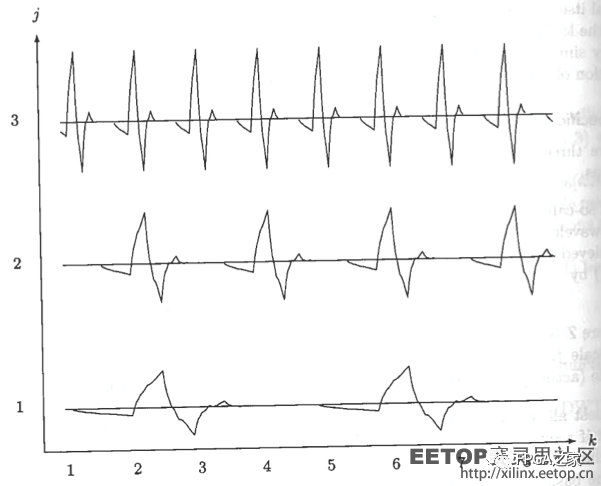
從這里看出，這里的縮放倍數都是2的級數，平移的大小和當前其縮放的程度有關。這樣的好處是，小波的basis函數既有高頻又有低頻，同時還覆蓋了時域。對于這點，我們會在之后詳細闡述。

小波展開的形式通常都是這樣(注意，這個只是近似表達，嚴謹的展開形式請參考第二篇)：

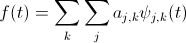
其中的

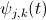
就是小波級數，這些級數的組合就形成了小波變換中的基basis。和傅立葉級數有一點不同的是，小波級數通常是orthonormal basis，也就是說，它們不僅兩兩正交，還歸一化了。小波級數通常有很多種，但是都符合下面這些特性：

1.小波變換對不管是一維還是高維的大部分信號都能cover很好。這個和傅立葉級數有很大區別。后者最擅長的是把一維的，類三角波連續變量函數信號映射到一維系數序列上，但對于突變信號或任何高維的非三角波信號則幾乎無能為力。

2. 圍繞小波級數的展開能夠在時域和頻域上同時定位信號，也就是說，信號的大部分能量都能由非常少的展開系數，比如a_{j,k}，決定。這個特性是得益于小波變換是二維變換。我們從兩者展開的表達式就可以看出來，傅立葉級數是

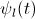
，而小波級數是

。

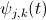
3. 從信號算出展開系數a需要很方便。普遍情況下，小波變換的復雜度是O(Nlog(N))，和FFT相當。有不少很快的變換甚至可以達到O(N)，也就是說，計算復雜度和信號長度是線性的關系。小波變換的等式定義，可以沒有積分，沒有微分，僅僅是乘法和加法即可以做到，和現代計算機的計算指令完全match。

可能看到這里，你會有點暈了。這些特性是怎么來的?為什么需要有這些特性?具體到實踐中，它們到底是怎么給小波變換帶來比別人更強的好處的?計算簡單這個可能好理解，因為前面我們已經講過正交特性了。那么二維變換呢?頻域和時域定位是如何進行的呢?恩，我完全理解你的感受，因為當初我看別的文章，也是有這些問題，就是看不到答案。要說想完全理解小波變換的這些本質，需要詳細的講解，所以我就把它放到下一篇了。

接下來，上幾張圖，我們以一些基本的信號處理來呈現小波變換比傅立葉變換好的地方，我保證，你看了這個比較之后，大概能隱約感受到小波變換的強大，并對背后的原理充滿期待:)

假設我們現在有這么一個信號：

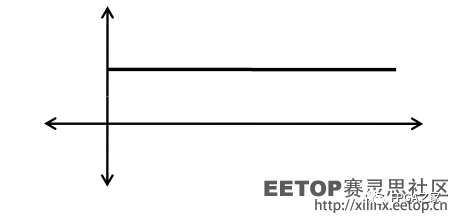
看到了吧，這個信號就是一個直流信號。我們用傅立葉將其展開，會發現形式非常簡單：只有一個級數系數不是0，其他所有級數系數都是0。好，我們再看接下來這個信號：

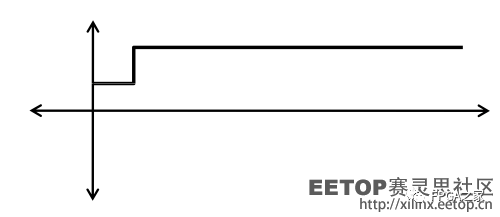
簡單說，就是在前一個直流信號上，增加了一個突變。其實這個突變，在時域中看來很簡單，前面還是很平滑的直流，后面也是很平滑的直流，就是中間有一個階躍嘛。但是，如果我們再次讓其傅立葉展開呢?所有的傅立葉級數都為非0了!為什么?因為傅立葉必須用三角波來展開信號，對于這種變換突然而劇烈的信號來講，即使只有一小段變換，傅立葉也不得不用大量的三角波去擬合，就像這樣：

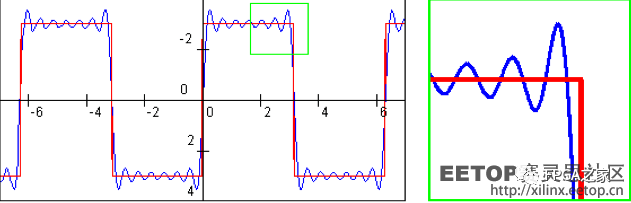
看看上面這個圖。學過基本的信號知識的朋友估計都能想到，這不就是Gibbs現象么?Exactly。用比較八股的說法來解釋，Gibbs現象是由于展開式在間斷點鄰域不能均勻收斂所引起的，即使在N趨于無窮大時，這一現象也依然存在。其實通俗一點解釋，就是當變化太sharp的時候，三角波fit不過來了，就湊合出Gibbs了:)

接下來我們來看看，如果用剛才舉例中的那種小波，展開之后是這樣的：

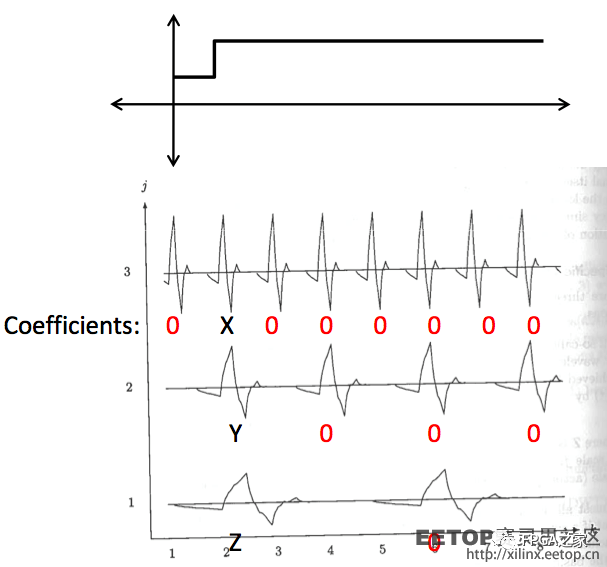
看見了么?只要小波basis不和這個信號變化重疊，它所對應的級數系數都為0!也就是說，假如我們就用這個三級小波對此信號展開，那么只有3個級數系數不為0 。你可以使用更復雜的小波，不管什么小波，大部分級數系數都會是0。原因?由于小波basis的特殊性，任何小波和常量函數的內積都趨近于0。換句話說，選小波的時候，就需要保證母小波在一個周期的積分趨近于0。正是這個有趣的性質，讓小波變換的計算以及對信號的詮釋比傅立葉變換更勝一籌!原因在于，小波變換允許更加精確的局部描述以及信號特征的分離。一個傅立葉系數通常表示某個貫穿整個時間域的信號分量，因此，即使是臨時的信號，其特征也被強扯到了整個時間周期去描述。而小波展開的系數則代表了對應分量它當下的自己，因此非常容易詮釋。

小波變換的優勢不僅僅在這里。事實上，對于傅立葉變換以及大部分的信號變換系統，他們的函數基都是固定的，那么變換后的結果只能按部就班被分析推導出來，沒有任何靈活性，比如你如果決定使用傅立葉變換了，那basis function就是正弦波，你不管怎么scale，它都是正弦波，即使你舉出余弦波，它還是移相后的正弦波。總之你就只能用正弦波，沒有任何商量的余地。而對于小波變換來講，基是變的，是可以根據信號來推導或者構建出來的，只要符合小波變換的性質和特點即可。也就是說，如果你有著比較特殊的信號需要處理，你甚至可以構建一個專門針對這種特殊信號的小波basis function集合對其進行分析。這種靈活性是任何別的變換都無法比擬的。總結來說，傅立葉變換適合周期性的，統計特性不隨時間變化的信號; 而小波變換則適用于大部分信號，尤其是瞬時信號。它針對絕大部分信號的壓縮，去噪，檢測效果都特別好。