協方差矩陣
方差衡量一個變量在自身之間的變化,而協方差衡量兩個變量(a和b)之間的變化。
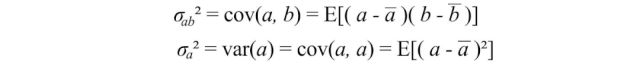
我們可以將所有可能的協方差組合保存在一個稱為協方差矩陣Σ的矩陣中。
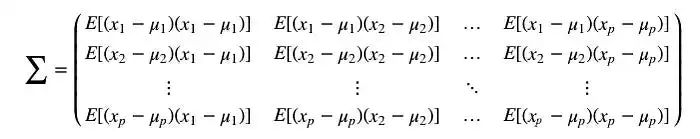
我們可以將這個簡單的矩陣形式重寫為:
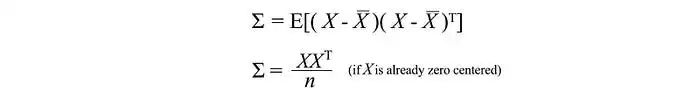
對角線元素保存單個變量(如身高)的方差,而非對角線元素保存兩個變量之間的協方差。現在讓我們計算樣本協方差。
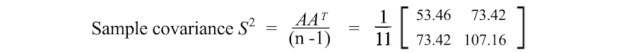

正的樣本協方差表明身高和體重是正相關的。如果它們是負相關的,協方差將為負數;如果它們是獨立的,則協方差為零。
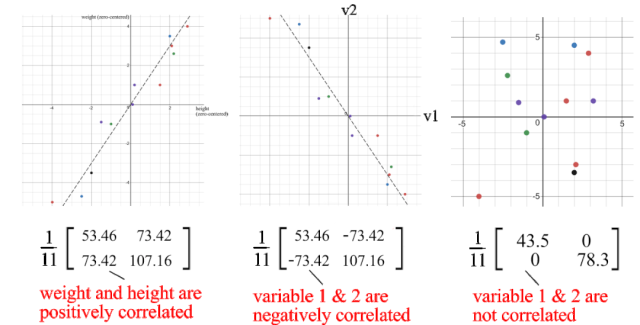
協方差矩陣和SVD
我們可以使用SVD來分解樣本協方差矩陣。由于σ?相對于σ?而言相對較小,我們甚至可以忽略σ?項。當我們訓練一個機器學習模型時,我們可以對身高和體重進行線性回歸,形成一個新屬性,而不是將它們視為兩個分離且相關的屬性(糾纏的數據通常使模型訓練更加困難)。
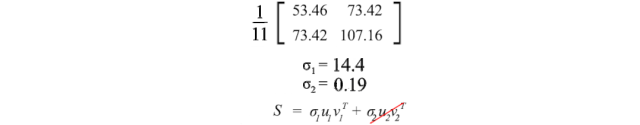
u?有一個重要的意義,它是S的主要成分。

在SVD的背景下,樣本協方差矩陣具有一些特性:
- 數據的總方差等于樣本協方差矩陣S的跡,這個值等于S的奇異值的平方和。有了這個,我們可以計算如果刪除較小的σ?項會損失多少方差。這反映了如果我們消除它們會丟失多少信息。
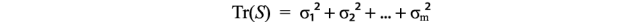
- S的第一個特征向量u?指向數據的最重要方向。在我們的例子中,它量化了體重和身高之間的典型比率。
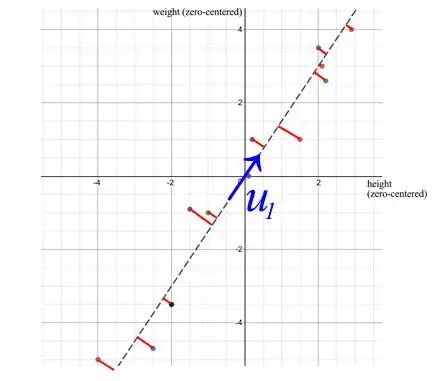
- 當使用SVD時,從樣本點到u?的垂直平方距離的誤差最小。
性質
協方差矩陣不僅對稱,而且還是正半定的。因為方差是正數或者零,所以u?Vu始終大于或等于零。通過能量測試,V是正半定的。
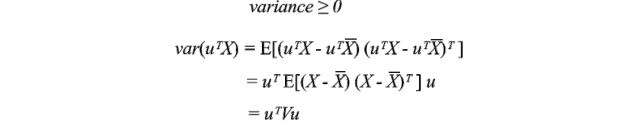
因此,
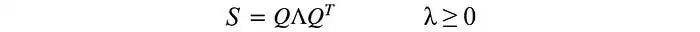
通常,在進行某些線性變換A之后,我們想知道轉換后數據的協方差。這可以用變換矩陣A和原始數據的協方差來計算。
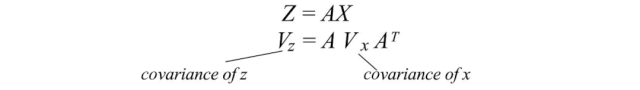
相關矩陣
相關矩陣是協方差矩陣的標準化版本。相關矩陣對變量進行標準化(縮放),使它們的標準差為1。
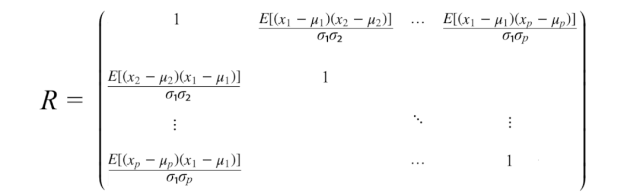
如果變量的量級相差很大,那么將使用相關矩陣。糟糕的縮放可能會損害梯度下降等機器學習算法的效果。
可視化
到目前為止,我們有很多方程式。讓我們將SVD的作用可視化,并逐漸開發我們的洞察力。SVD將矩陣A分解為USV?。將向量x(Ax)應用于A可以被視為對x執行旋轉(V?),縮放(S)和另一個旋轉(U)。
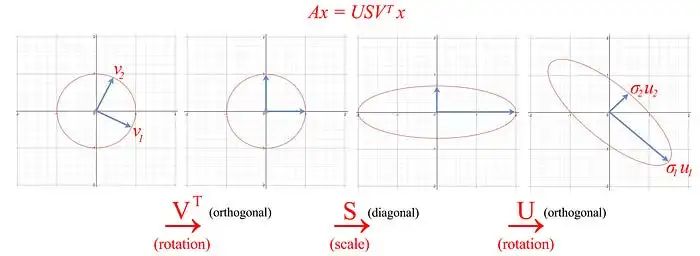
如上所示,矩陣 V 的特征向量 v? 被轉換為:
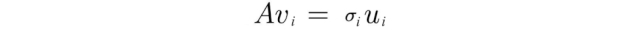
或者以完整矩陣形式表示
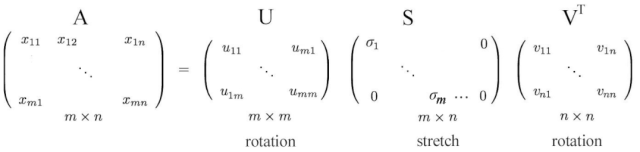
r = m < n
奇異值分解(SVD)的洞察
如前所述,SVD 可以表示為
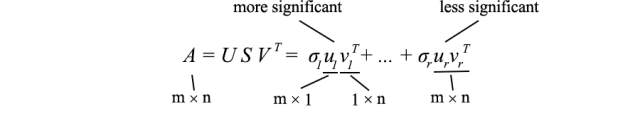
由于 u? 和 v? 的長度為單位長度,確定每個項的重要性的最主要因素是奇異值 σ?。我們故意按降序對 σ? 進行排序。如果特征值變得太小,我們可以忽略剩下的項(+ σ?u?v?? + …)。
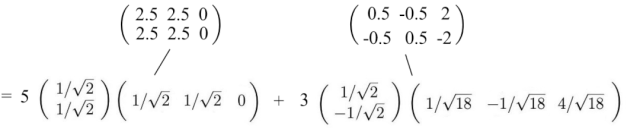
這種表示法具有一些有趣的含義。例如,我們有一個矩陣,其中包含不同投資者交易的股票收益率。

作為基金經理,我們可以從中獲取什么信息?尋找模式和結構將是第一步。也許,我們可以找到具有最大收益的股票和投資者的組合。SVD 將 n × n 矩陣分解為具有奇異值 σ? 表示其顯著性的 r 組件。將其視為一種將糾纏和相關屬性提取到更少的無關聯的主要方向的方法。
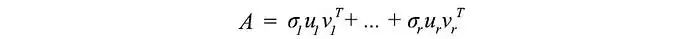
如果數據高度相關,我們應該期望許多 σ? 值較小且可以忽略。
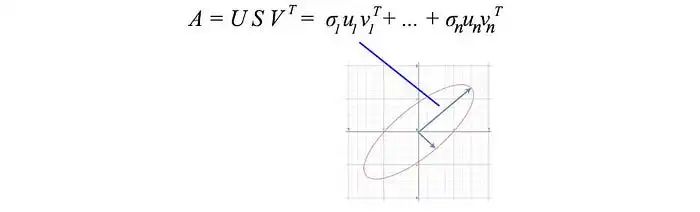
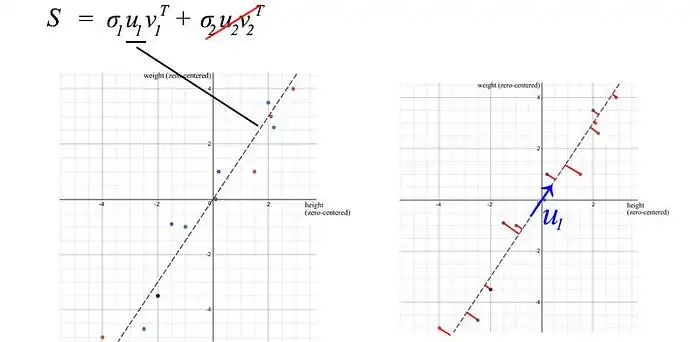
在我們之前的例子中,體重和身高高度相關。如果我們有一個包含 1000 人體重和身高的矩陣,SVD 分解中的第一個組件將占主導地位。如我們之前討論的那樣,u? 向量確實表示了這 1000 人之間體重和身高的比例。
主成分分析(PCA)
從技術上講,SVD 分別提取具有最高方差的方向中的數據。PCA 是將 m 維輸入特征映射到 k 維潛在因子(k 個主成分)的線性模型。如果我們忽略不太重要的項,我們將去除我們不太關心的組件,但保留具有最高方差(最大信息)的主要方向。
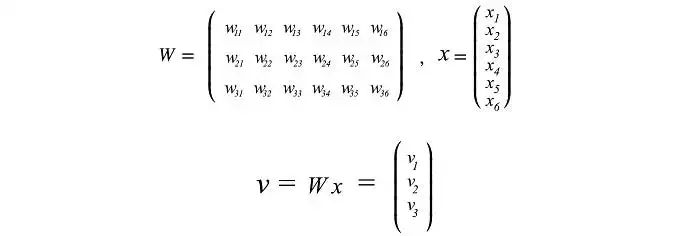
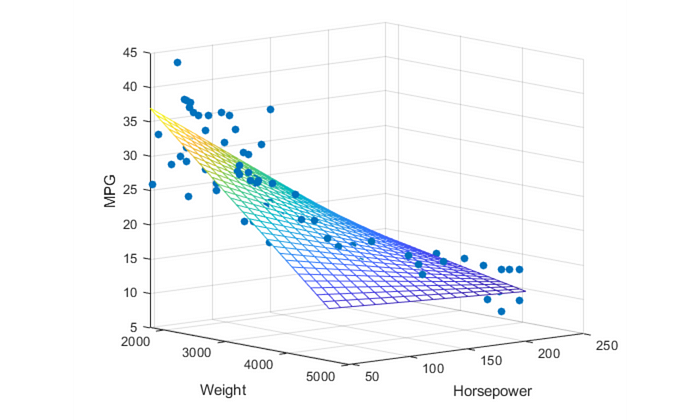
考慮下面顯示為藍色點的三維數據點。它可以很容易地用一個平面來近似。
您可能很快就會意識到,我們可以使用 SVD 找到矩陣 W。考慮下面位于二維空間的數據點。
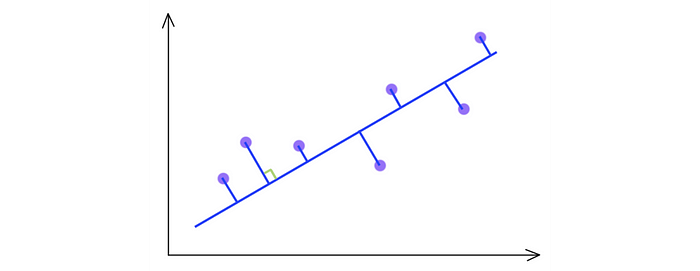
SVD 選擇最大化輸出方差的投影。因此,如果 PCA 具有更高的方差,它會選擇藍線而不是綠線。
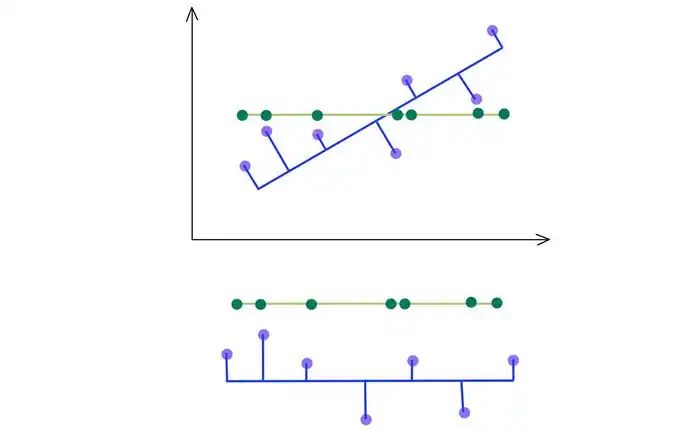
如下所示,我們保留具有前 kth 最高奇異值的特征向量。
利率
讓我們通過回顧一個關于利率數據的例子來更深入地說明這個概念,該數據源自美國財政部。從 3 個月、6 個月、…到 20 年的 9 種不同利率(基點)在連續 6 個工作日內進行了收集,其中 A 存儲了與前一天相比的差異。A 的元素在此期間已經減去了其平均值。即它是零中心的(沿著其行)。
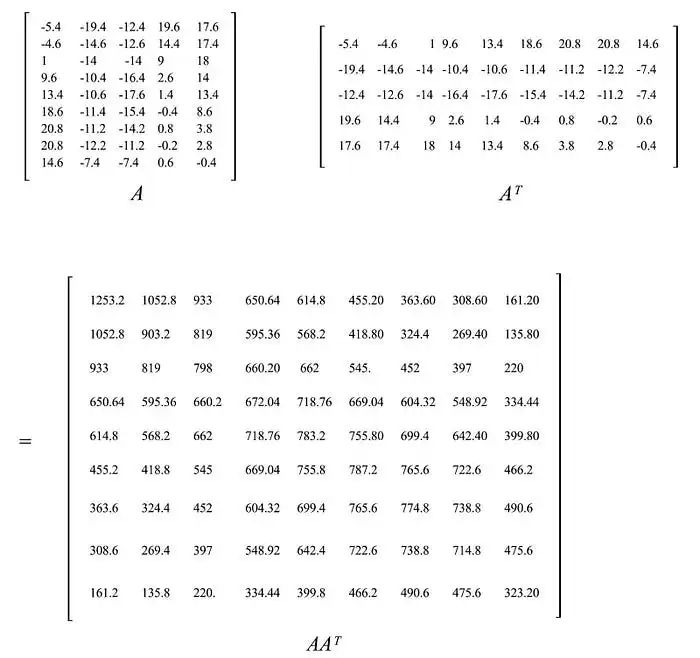
樣本協方差矩陣等于 S = AA?/(5-1)。

現在我們有了想要分解的協方差矩陣 S。SVD 分解為

從 SVD 分解中,我們意識到我們可以關注前三個主成分。
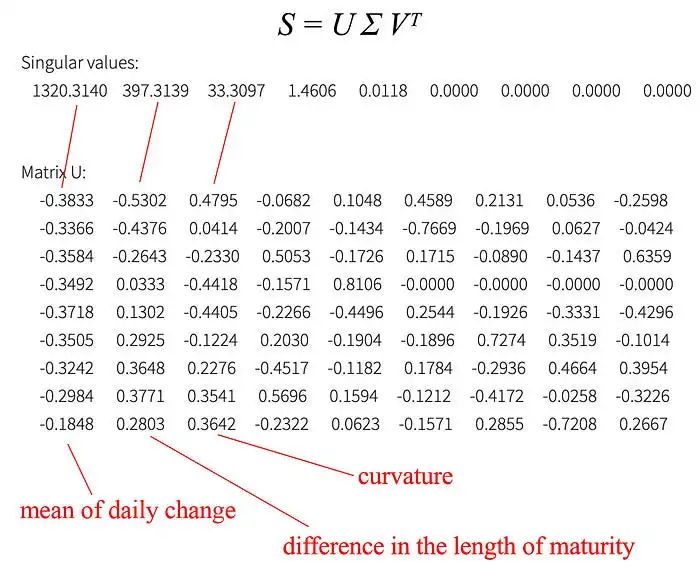
如圖所示,第一個主成分與所有到期長度的日常變化的加權平均值有關。第二個主成分調整了與債券到期長度敏感的日常變化。(第三個主成分可能是曲率 - 二階導數。)
我們在日常生活中很了解利率變化和期限之間的關系。因此,主成分重新確認了我們相信利率如何運作。但是當我們面對陌生的原始數據時,PCA 對于提取數據的主成分以找到底層信息結構非常有幫助。這可能回答了如何在大海撈針的一些問題。
提示
在執行 SVD 之前,對特征進行縮放。
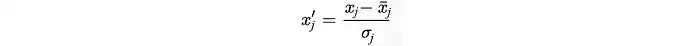
假設我們想保留 99% 的方差,我們可以選擇 k,使得
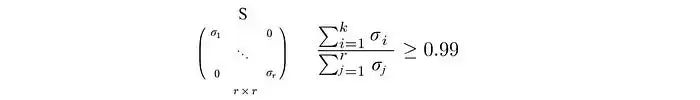
-
SVD
+關注
關注
0文章
21瀏覽量
12181 -
機器學習
+關注
關注
66文章
8425瀏覽量
132774 -
線性代數
+關注
關注
5文章
50瀏覽量
11112
發布評論請先 登錄
相關推薦
基于改進奇異值分解的人耳識別算法研究
采用奇異值分解的數字水印嵌入算法
《工程線性代數(MATLAB版)》程序集
基于整體與部分奇異值分解的人臉識別
基于奇異值分解的車牌特征提取方法研究
機器學習進階之線性代數-奇異值分解(上)





 機器學習進階之線性代數-奇異值分解(下)
機器學習進階之線性代數-奇異值分解(下)











評論