時序電路的考察主要涉及分析與設計兩個部分,上文介紹了時序邏輯電路的一些分析方法,重點介紹了同步時序電路分析的步驟與注意事項。 本文就時序邏輯電路設計的相關問題進行討論,重點介紹時序邏輯電路的核心部分——計數器。
計數器的分類
所謂計數器,就是在技術脈沖的驅動下,一次進行加1或者減1計數的時序邏輯電路。 總體來說,由上文時序邏輯電路的分析中可以得知,時序邏輯電路包括同步電路與異步電路兩種,因此計數器也要分為同步計數器和異步計數器,計數器又因計數順序不同分為加法計數器與減法計數器,每種計數器的計數規則不同又出現了進制.... 這樣的不同造成了在設計計數器時組合電路的設計與觸發器的選型都有著很多的不同,因此熟悉各種類型的計數器時實現計數器設計的基礎。
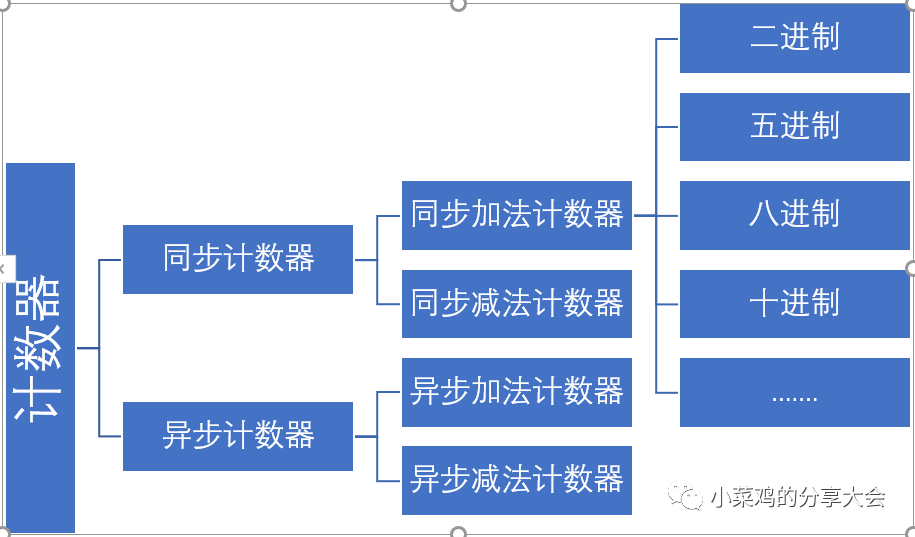
同步計數器
同步計數器的設計核心就是利用幾個同步的觸發器和一定的門電路將需求的真值表循環輸出,這里需要注意的是,每一位數都是由一個觸發器實現的,比如我要實現的是一個三位二進制數(也就是八進制),那么我一定需要使用3個觸發器依次表示由高到低的三位數字,而且設計一定是由低位到高位進行,并且依據每一位的變化情況選擇合適的觸發器實現對應的功能, 因此選擇觸發器成了相當重要的一步。
從個人淺薄的設計經驗來講,一般的計數器都能夠利用T觸發器或D觸發器來實現,并且相對于其他觸發器能夠達到最簡的設計思路。 如果題目明確要求使用JK觸發器,做法一是直接套用卡諾圖化簡的方法找每個JK對應的邏輯函數,然后利用JK觸發器的特征方程搭建電路,二是把JK兩端直接接在一起就成為了T觸發器,這樣的做法極大的簡化了設計的過程,不需要繁瑣的卡諾圖化簡和方程對應,其中便利可自行設計體會,如第七次實驗內容的第三問。
同步三位二進制加法計數器
以三位二進制加法計數器為例進行簡單的設計介紹,首先根據需求列真值表,這是設計所有計數器電路的第一步,如圖
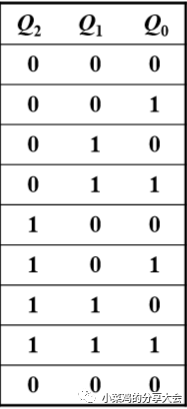
首先看Q0,很明顯的觀察到,每一個脈沖都會使Q0反轉,也就是T'觸發器的特性(這里直接體現了掌握各種觸發器的特性的重要性,不熟練的小伙伴建議先去看看之前的關于觸發器的幾篇推文),所以第一個T'觸發器的輸出就是Q0。
接下來看Q1這一列,還是存在規律的反轉,但是這里不要看他是每兩個翻轉一次這個事情,對于同步電路設計而言用處不大,而是要找這個反轉和其他幾個Q之間的關系,比如這里就是在Q0=1的情況下Q1才會反轉。 在這里建議
一個暫時的設計原則:在同一個電路的設計當中,盡量所有的觸發器都選擇同樣的一種,這樣做的目的是減少思考量。 所以這里我們依然采用T觸發器(T'就是T觸發器的輸入端T始終接1),那也就是說本來的T'觸發器是來一個脈沖就要變化,現在的是要在Q0=1的時候再來脈沖才變化,所以就是在Q0=1的時候成為T'嘛,因此令T=Q0。
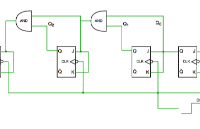
同理,我們看到真值表中的Q2只有在Q0和Q1同時為1的情況下才變化,所以T=Q1Q0,最后不要忘記進位端的設計,逢111進1,所以進位C=Q2Q1Q0.這樣我們就完成了設計(因為這里沒有無效態,所以不需要自啟動檢查)。 如圖
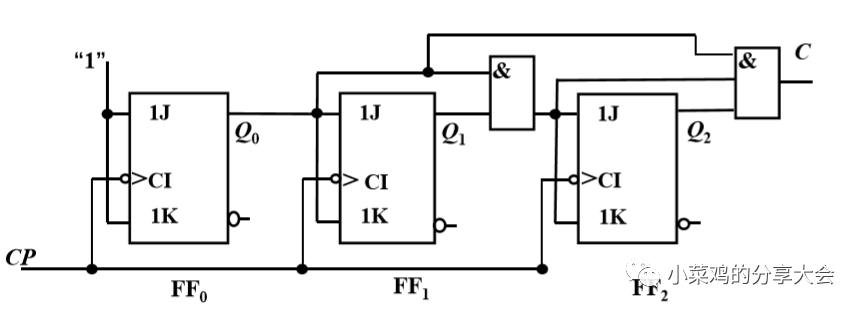
同步十進制加法計數器
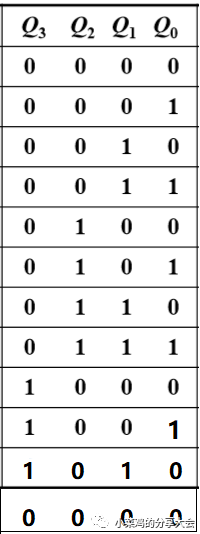
上面介紹的三位二進制計數器正好滿足了三位計數器所有的八個狀態,即不存在無效態。 但是在很多的設計中,我們并不能使用所有的狀態,存在的無效態我們需要將其跳過主循環并能夠自啟動,比如七進制,十進制,這里我們以十進制加法計數器作為例子進行介紹。
首先還是要列真值表,如圖
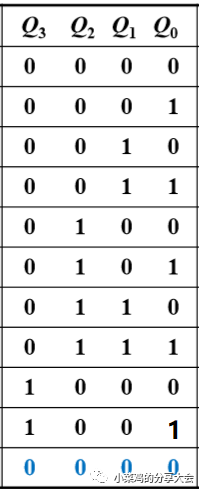
這里很明顯的體現出來了狀態的未完全使用。 四位二進制可以表述16個狀態,即0000--1111,但是我們在這里只使用了前10位,即0000--1001,從1001直接回到0000,但是整體的設計思路和上一個沒有很大的區別,仍然是從低位到高位依次設計。
首先觀察到Q0依然是交替變化,所以仍然用T'。 其次Q1的大體變化仍然同上一個近似,不同點在于最后一個的變化,這時的Q0=1,但是Q1沒有反轉,這里需要意識到的是不僅僅需要看低位的現態,還要看別的位的現態,找到最特殊的點,這里的特殊點就是Q3=1,之前在Q1變化的時候Q3都是0,因此T1不簡單的等于Q0,而同時要保證Q3=0,即為T1=Q0Q3(非)。 剩余兩個依次類推。 方程與電路如下:
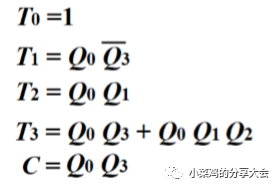
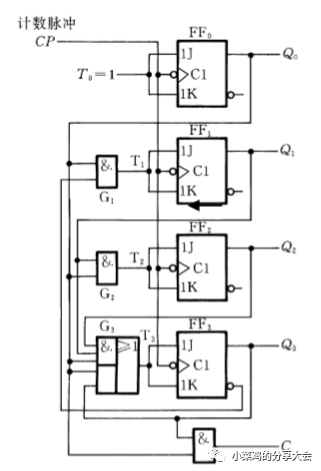
-
邏輯電路
+關注
關注
13文章
502瀏覽量
43224 -
電路設計
+關注
關注
6701文章
2530瀏覽量
213553 -
計數器
+關注
關注
32文章
2288瀏覽量
96137 -
觸發器
+關注
關注
14文章
2033瀏覽量
61956 -
時序邏輯電路
+關注
關注
2文章
94瀏覽量
16793
發布評論請先 登錄
【FPGA開源教程連載】第三章 時序邏輯電路設計之計數器
Multisim的時序邏輯電路設計仿真




















評論