在討論50歐姆阻抗這個話題時,有同學留言說:是不是和最大輸出功率也相關,今天我們從阻抗匹配角度來談一談 最大輸出功率這個話題。
阻抗匹配問題一直是射頻設計中一個最基本的問題,任何射頻設計都繞不開阻抗匹配。
匹配的終極目的就是使得電磁波信號能夠在系統中無反射的向前傳播。 在很多時候,我們都忽略了反射的影響,其實不然,在微波元器件中,我們除了要關注插入損耗外,反射損耗也是必須要關注的。 很多情況下,反射損耗對系統的影響更大。 反射損耗另一個比較熟悉的名字就是回波損耗——RL。
最大功率傳輸的必要條件是:負載阻抗和源阻抗共軛匹配,就是下面這個方程式
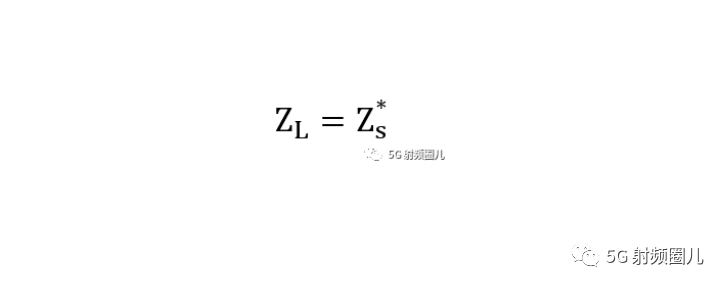
這樣匹配有什么好處呢?
1,負載匹配,可以向負載傳輸最大的功率。
2,接收機端進行阻抗匹配能夠改善接收機的噪聲系數
3,發設計端進行阻抗匹配,能夠傳輸最大功率,提高效率。
說起共軛匹配,我們先復習一下共軛的概念。
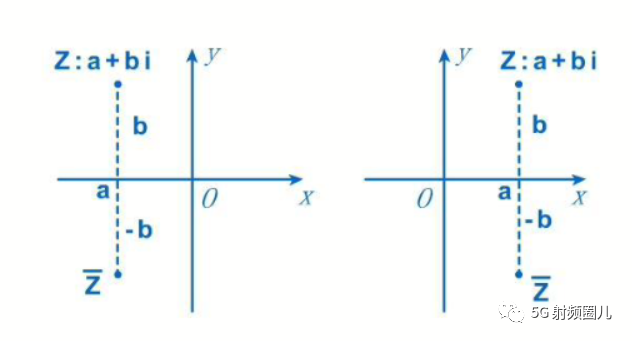
一提到數學就頭疼,共軛是什么玩意? 帶大家一起回憶一下。 共軛就是兩個復數的實部相同,虛部符號相反,大小相等,如下圖所示,在復平面上,共軛也就是在坐標系里沿著x軸(實軸)鏡像了一下。
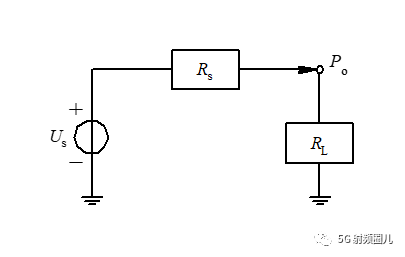
實現最大功率傳輸,為什么要共軛呢? 我們一起看一下。 假設在一個最簡單的電路中,如下圖所示,Us為信號源電壓,Rs為信號源內阻,RL為負載電阻。 在什么情況下才能夠使得信號源把最多的功率提供給負載呢? 也就是如何讓信號源的輸出功率盡可能大。
利用上面這個簡單的電路,很容易得到信號源輸出功率與電路元器件之間的關系:
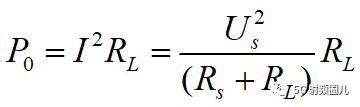
在這里,我們假設:
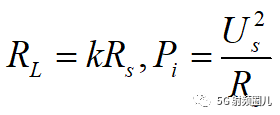
這時,我們就可得到:
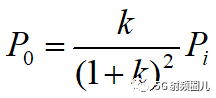
我們就得到了,信號源的輸出功率只取決于Us,Rs和RL。 當信號源一定時,輸出功率只取決于k,負載阻抗和信號源內阻的比值。
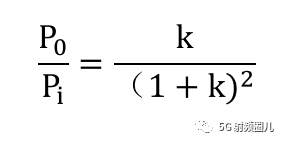
取右邊的極值唄。 我們也可以得到這個功率比和阻抗比的關系曲線。
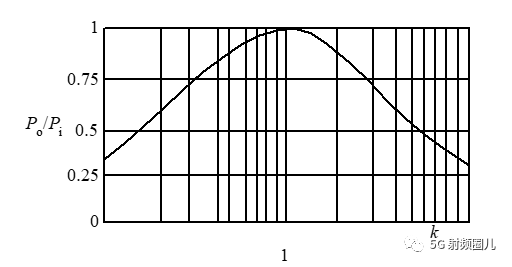
也就是當k等于1時,即RL=Rs時,負載可獲得最大的輸出功率,此時的狀態為匹配狀態。 無論負載阻抗大于還是小于信號源內阻,都不可能使得負載獲得最大功率,并且這兩個電阻值偏差越大,輸出功率就越小。
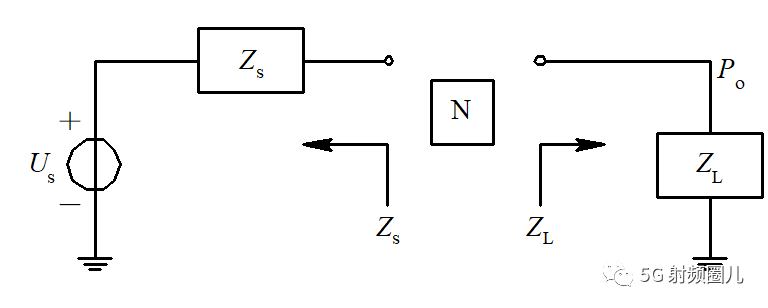
當源阻抗為復數時,我們可以用同樣的推導過程進行計算。 這時的等效電路如下圖所示:
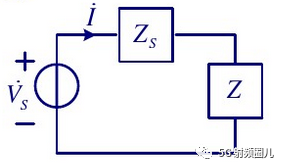
其信號源電壓為Vs,信號源內阻為Zs=Rs+jXs。 負載阻抗為Z=R+jX。 電路中的電流為:
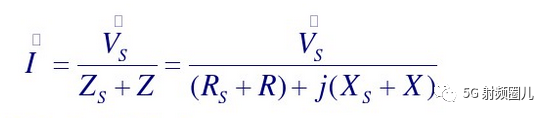
電流的幅度值為:
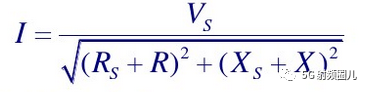
負載處的功率為:
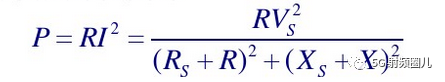
參照前文到的結論,當R=Rs,X=-Xs時,負載的功率最大,即輸出功率最大。 這時即有
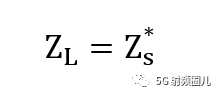
那么在共軛匹配下,負載能夠得到最大的功率是多少呢?
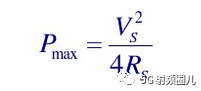
只有二分之一的源功率能夠到負載,剩下的到哪去了呢? 被源自己的電阻吃掉了。 所以我們經常會發現,源都是最熱的那一個。
如果負載阻抗不能滿足共軛匹配條件怎么辦呢? 很簡單,讓他匹配嘛,在源與負載之間加一個匹配網絡,將負載阻抗變換為信號源阻抗的共軛匹配。 這個阻抗變換就是阻抗匹配的重要方法之一。
注意:看看過去的方向。
審核編輯:湯梓紅
-
阻抗匹配
+關注
關注
14文章
358瀏覽量
31445 -
歐姆
+關注
關注
0文章
82瀏覽量
21656 -
輸出功率
+關注
關注
0文章
110瀏覽量
14926 -
電磁波
+關注
關注
21文章
1484瀏覽量
54739
原文標題:為什么要共軛匹配?
文章出處:【微信號:電子資料局,微信公眾號:電子資料局】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
為什么要阻抗匹配?

掃盲啦!新手福利不要錯過——阻抗匹配基礎知識詳解
改進的并行廣義共軛殘差算法
基于預條件共軛梯度法的混凝土層析成像
用FPGA實現共軛變換圖像處理方法




















評論