應用背景

1970年，Bockris在《Mordern Electrochemistry》一書中把電化學定義為：研究帶電界面的現象的科學，及研究電子導體和離子導體界面現象的科學。利用第一性原理計算探究界面反應機理，是目前廣泛應用的研究手段之一。

在電化學界面反應過程中，由于電化學反應界面通常與恒定電極電勢的外電極相連，為確保電子的化學勢與外電極的電勢達到平衡，即電子的巨正則系綜（grand canonical ensemble），實際體系中會存在電子的流入與流出過程。傳統的第一性原理計算通常是在正則系綜下，即在電荷守恒的條件下展開的，因此它并不能很好的描述電化學界面反應，下文中我們將在電荷守恒的條件下展開的計算模型稱為恒電荷模型（constant charge model，CCM）。

因恒電荷模型并不適于處理電化學界面問題，我們可采用在電子巨正則系綜下展開第一性原理計算，這種計算方法又被稱為固定電勢方法（fixed potential method/constant potential method）。在下文中我們將利用固定電勢計算的模型稱為恒電勢模型（constant potential model，CPM）。

后文提供了使用DS-PAW計算電催化氮還原反應（Electrocatalytic nitrogen reduction reaction, eNRR）過程中反應能計算的詳細教程。

案例概覽

本文展示了如何使用DS-PAW模擬一個電催化還原氮氣反應。該反應以碳基負載過渡金屬Ru單原子為催化劑，使用DS-PAW對電催化N2分子的吸附及還原過程進行模擬。在計算過程中使用了CCM_vacuum，CCM_water，CPM_water三種不同的模型，本文詳細介紹了在不同模型下如何設置參數及計算反應能。

更多關于DS-PAW的使用細節，請移步DS-PAW手冊查看。

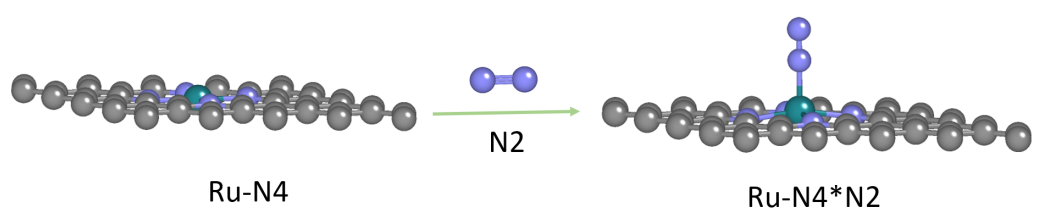
圖1. 吸附過程示意圖

計算流程

DS-PAW模擬的反應為 N2 分子在碳基負載Ru單原子上的吸附過程，反應的表達式可簡寫作：(Ru ? N4 ) + N2 = (Ru? N4 ? N2 )

第一步：搭建模型

模型包括：(a) 碳基負載Ru原子模型(Ru ? N4) ，(b) N2單分子模型，(c) 吸附了 N2 分子的碳基負載Ru原子模型(Ru? N4 ? N2)

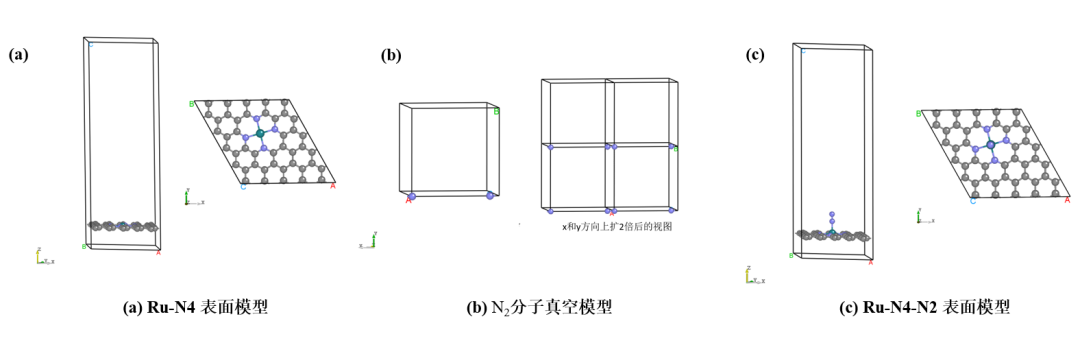
圖2.計算模型圖

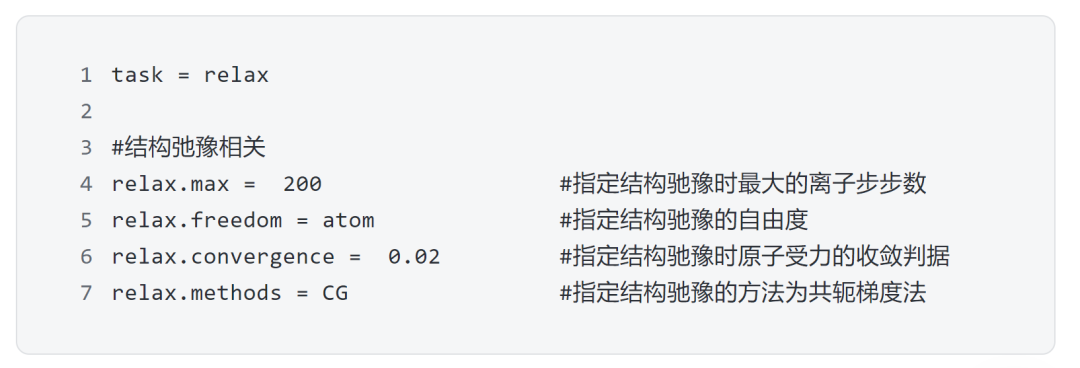
第二步：結構弛豫

對搭建的結構進行結構弛豫，獲得穩定結構，在DS-PAW中進行結構弛豫需要的核心參數：

第三步：能量計算

在不同模型條件下進行能量計算，獲得穩定構型對應能量，下面按不同模型分別進行介紹：

CCM_vacuum

常規的真空層下的scf計算，即可獲得CCM_vacuum模型下的能量，下面列出了在DS-PAW中進行單點能計算需要設置的核心參數：

CCM_water

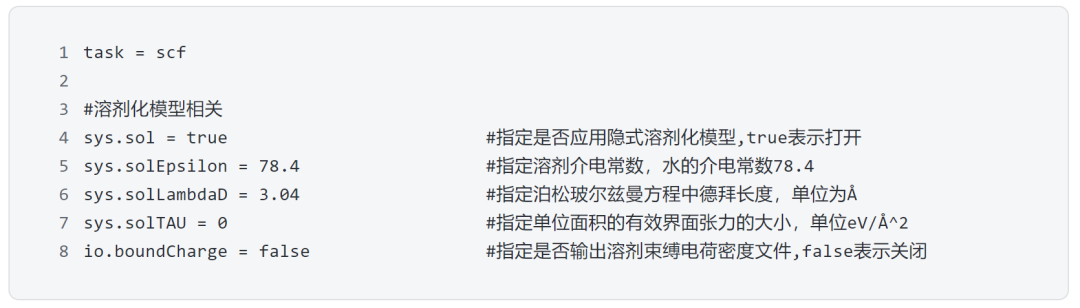
在CCM模型下，也可以利用隱式溶劑化模型來考慮溶劑效應，這里我們以水溶液為例，列出利用DS-PAW在scf計算中引入溶劑化模型所需要設置的核心參數：

CPM_water

在DS-PAW中用固定電勢方法計算即可獲得CPM模型下的能量。在新發布的2023A版本中進行固定電勢計算必須引入溶劑化模型，這里列出了利用DS-PAW在隱式水溶液環境下進行固定電勢計算的核心參數：

第四步：反應能計算

本文選取了3個不同的計算模型，首先介紹各模型下的吸附反應式：

CCM_vacuum:

該模型下，吸附反應式可寫作:

(Ru-N4)＋N2 (ideal gas)＝(Ru-N4-N2)

我們定義ΔE為反應能，反應能的計算表達式為：

ΔE＝E0(Ru-N4-N2)-E0(Ru-N4)-E0(N2)

其中，E0對應真空模型下體系的總能（(sigma→0），該數值可從自洽計算所得的scf.h5（或system.json）文件中獲取，查找關鍵字 “TotalEnergy0” 即可。

CCM_water：

該模型下，吸附反應式可寫作:

(Ru-N4)(in water)＋N2 (ideal gas)＝(Ru-N4-N2) (in water)

ΔE＝E0(Ru-N4-N2)-E0(Ru-N4)-E0(N2)

其中，E0對應水溶液浸潤的模型下體系的總能（(sigma→0），該數值可從自洽計算所得的scf.h5（或system.json）文件中獲取，查找關鍵字 “TotalEnergy0” 即可。

CPM_water 該模型下模擬的反應過程為氣相中的N2在由水溶液浸潤并與0V vs. SHE(標準氫電極)電極接觸的催化劑表面的吸附過程，此時吸附反應式有兩種寫法，為便于描述，我們定義了以下物理量符號：

ne0 : 中性體系下的核電荷數

ne : 當體系電壓為設定值(sys.fixedPPotential所設數值,此例對應 0 V)時體系的總電子數

dne : 當體系電壓為設定值時，體系的帶電量：dne = ne ? ne0

μe : 體系電子化學勢，電勢零點為溶液深處（即DFT計算得到的電荷密度最低點的電勢值）

Δe : 吸附態體系價電子數(eAB)與吸附基底和吸附分子總價電子數(eA+eB)的差值

Ω0 : grand total energy(sigma→0): 電子巨正則系綜下的體系總能，其表達式為：Ω0 = E0 ? dne ? μe

此時，CPM_water模型下吸附反應式可參考如下寫法：

方法一、在反應式中考慮 Δe ，吸附反應式可寫作:

Ru-N4 (0V vs. SHE) + N2(ideal gas) = Ru-N4-N2 (0V vs. SHE) - Δe

ΔE = E0(Ru-N4-N2) ? Δe * μe ? E0(Ru-N4) ? E0(N2)

其中，E0的數值可從自洽計算所得的 scf.h5（或system.json）文件中獲取，查找關鍵字 “TotalEnergy0” 即可。

ne 和 μe 的數值可從自洽計算所得的 DS-PAW.log （或 scf.h5 或 system.json）文件中獲取，最后一個LOOP下查找關鍵字 “Electron” 和 “Chemical Potential(electron) ” 即可。

方法二、考慮電子巨正則系綜下的體系總能 Ω0

由于固定電勢計算是模擬的電子的巨正則系綜，此時反應能計算式中的體系總能 E0 應當用Ω0 來代 替。吸附反應式可寫作:

(Ru-N4) (0V vs. SHE) + N2(ideal gas) = (Ru-N4-N2) (0V vs. SHE)

ΔE = Ω0 (Ru-N4-N2) ? Ω0 (Ru-N4) ? Ω0 (N2)

其中，Ω0 的數值可從自洽計算所得的DS-PAW.log （或 scf.h5 或 system.json）文件中獲取，最后一個LOOP下查找關鍵字 “Grand Total Energy” 即可。

由于(Ru-N4)與(Ru-N4-N2)的電勢為0V vs. SHE，故對(Ru-N4)與(Ru-N4-N2)進行0V下的固定電勢計算，從DS-PAW的相應輸出文件提取數據，得到如下表格，能量單位為 eV：

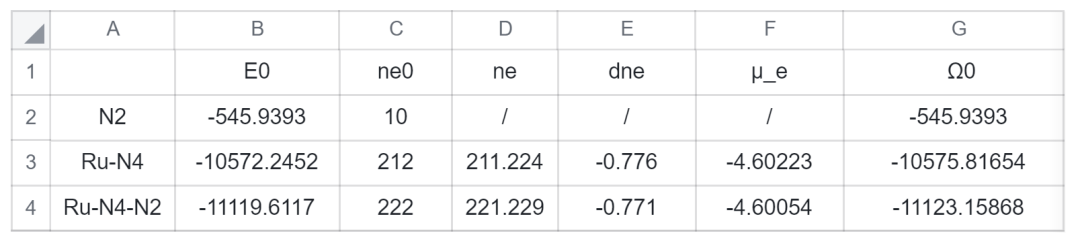
表 1. CPM_water模型下固定電勢計算數據

接下來將表1的數據代入對應的表達式中進行計算：

方法一、在反應式中考慮 Δe ，反應能計算過程如下:

Ru-N4 (0V vs. SHE) + N2(ideal gas) = Ru-N4-N2 (0V vs. SHE) - Δe

ΔE = E0(Ru-N4-N2) ? Δe * μe ? E0(Ru-N4) ? E0(N2)

= ? 11119.6117 ? (221.229 ? 211.224 ? 10) × ( ? 4.600) ? ( ? 10572.2452) ? ( ? 545.9393)

= ? 1.4042 eV

方法二、考慮電子巨正則系綜下的體系總能 Ω0 ，反應能計算過程如下:

(Ru-N4) (0V vs. SHE) + N2(ideal gas) = (Ru-N4-N2) (0V vs. SHE)

ΔE = Ω0 (Ru-N4-N2) ? Ω0 (Ru-N4) ? Ω0 (N2)

= ? 11123.1586 ? ( ? 10575.8165) ? ( ? 545.9393)

= ? 1.4027 eV

通過兩種方法計算所得的吸附能一致。可見?DS-PAW中定義的Ω0即可很方便的計算固定電勢下的反應能。

結果展示

將表1的數據分別代入CCM_vacuum、CCM_water、CPM_water模型的吸附反應式，計算三個模型下，eNRR前三步反應的反應能，結果如下表2所示：

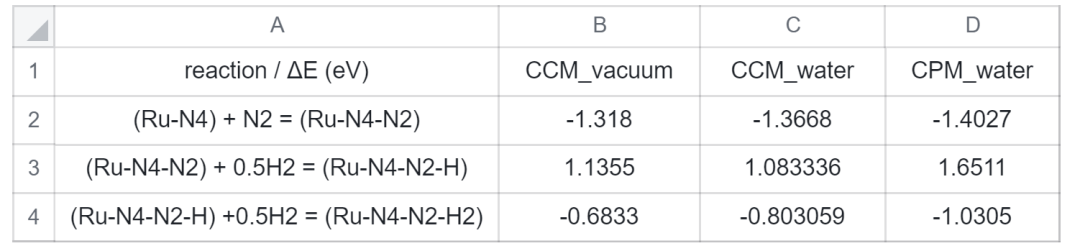
表 2. 反應能數據表

最后將上述結果繪制成反應坐標曲線，效果如下圖3所示：

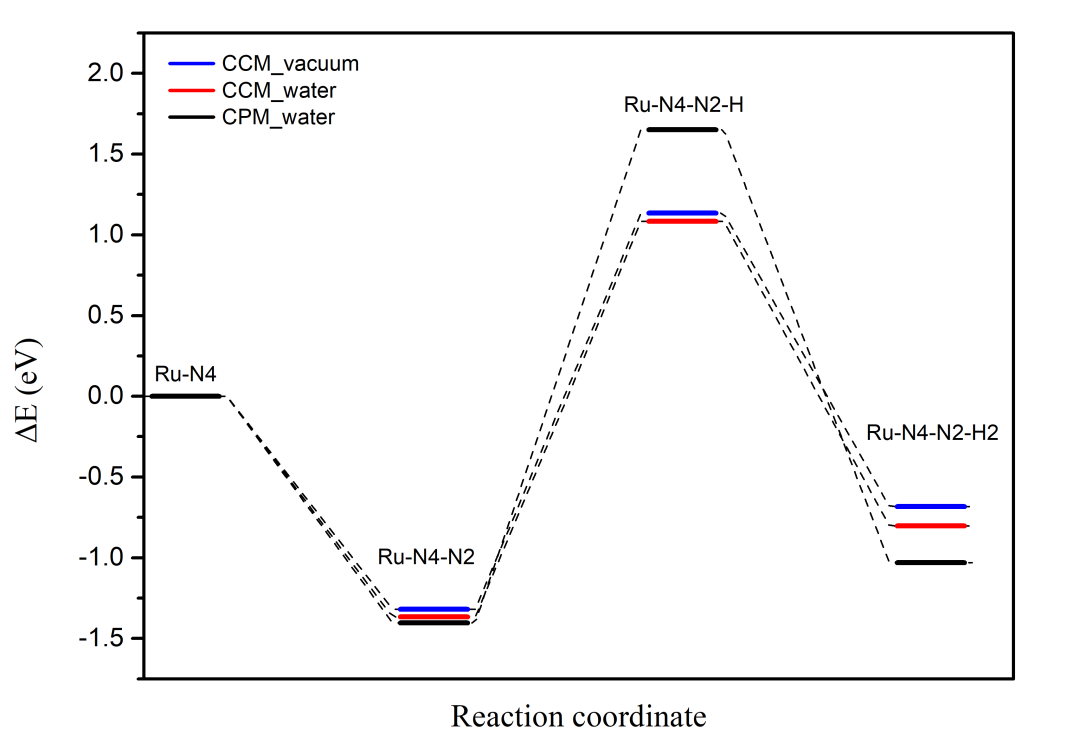
圖 3. 反應坐標-反應能曲線

審核編輯：劉清