1. 濾波的目的
在信號的實時處理中,濾波是十分必要的,因為信號中難免會由于各種原因混入噪聲,干擾我們對信號進行分析。
這里強調了“實時”,是因為在一些場景中,我們可能需要對信號進行離線的、交互式的分析,此時僅僅是對原始信號進行采集即可,無需軟件 進行濾波,只需要硬件在采集信號時做一下抗混疊濾波即可,這種場景不是本文所關心的。
在更多的場景下,比如我們的運動手表、手環在處理ppg信號計算心率時,是會進行實時計算的,那么就會進行實時濾波處理:因為大多數人的心率頻率在0.7~3.6Hz范圍內,至少在這之外的頻率會在計算心率之前濾除掉。
2. 信號模擬
比如我們要處理一個信號,但是我們僅僅關心信號100Hz以下的頻段,這時我們就需要一個低通濾波器了,此時我們先模擬出一個包含5Hz和3000Hz頻率成分的信號,假設信號采樣頻率為8192,采樣時間為1秒,共計8192個點。信號生成和展示的代碼如下:
import numpy as np
from numpy import cos
import matplotlib.pyplot as plt
pi = np.pi
t = np.linspace(0, 1, 8192)
signal = 3 * cos(2 * pi * 5 * t + pi/3) + 7 * cos(2 * np.pi * 3000 * t + 3/8*pi)
plt.figure()
plt.plot(t, signal)
plt.show()
我們生成了這樣的一個信號:
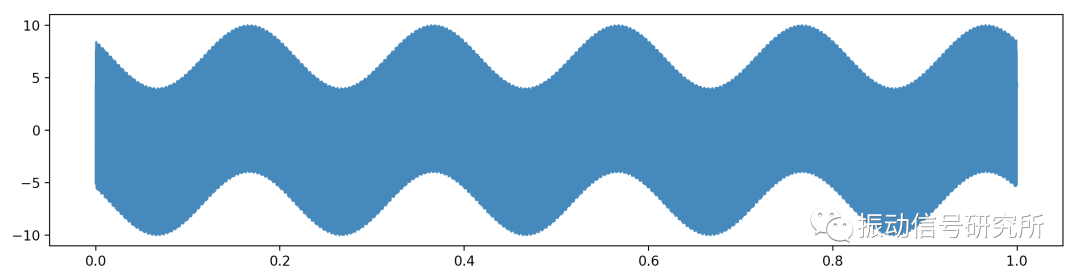
生成的信號
3. FIR濾波器系數生成
這一步可以使用matlab進行輔助,本文僅僅是想要一個截止頻率為10Hz的FIR低通濾波器,步驟如下:
- 打開matlab;
- 點擊"APP";
- 找到濾波器設計工具,并點擊;
- 選擇響應類型、設計方法、階數等。
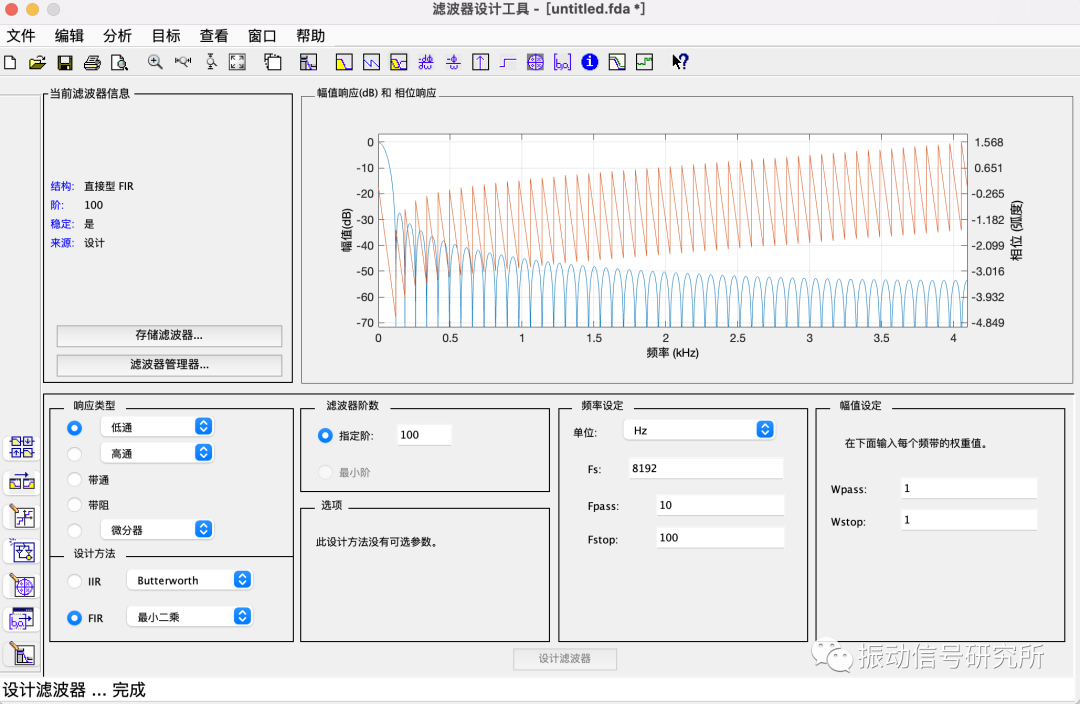
輔助設計界面
- 點擊“文件” 、“導出”、“系數文件”,導出系數文件,我把導出的系數(FIR低通濾波系數僅有分子)畫出來后如下圖:
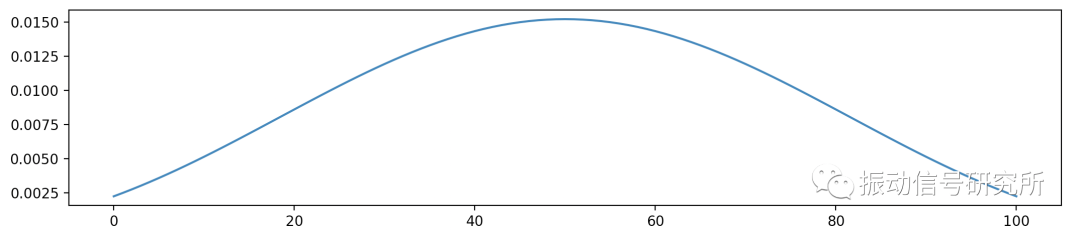
系數波形圖
3. FIR濾波原理
采用FIR進行濾波,從操作上看是進行卷積操作,對上述濾波器的系數進行FFT變換即可窺見一斑:
import numpy as np
import matplotlib.pyplot as plt
# b = [......] 101個系數組成的列表,此處省略
delta_f = 1
plt.plot([delta_f * i for i in range(4097)], abs(np.fft.rfft(b, 8192))) # 單邊FFT
plt.show()
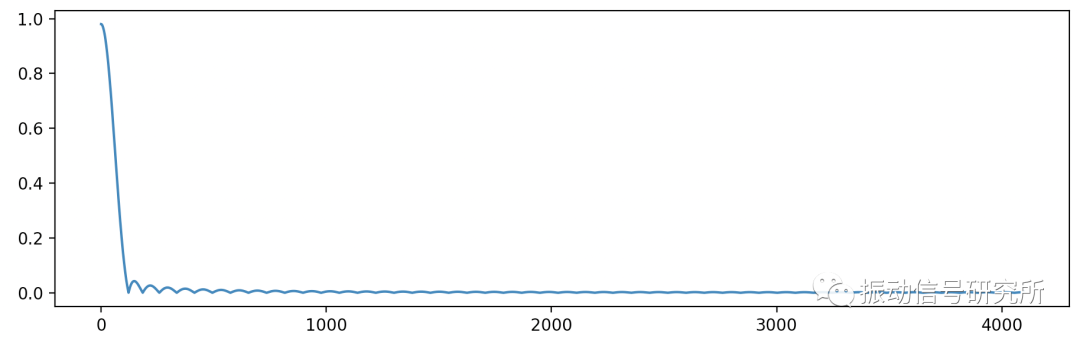
系數的傅里葉變換
這里得到的就是濾波器的幅頻響應曲線,和濾波器輔助設計工具中所展示的幅頻響應曲線是一致的。
4. 濾波計算代碼與結果
把第二步生成的信號中高于100Hz的頻率成分(即3000Hz的成分)濾除,得到的結果如下圖所示,在結果的開頭和結尾產生了失真,這是因為在卷積運算過程中,在剛開始和結尾計算時有效信息不足進行了補零操作導致的。
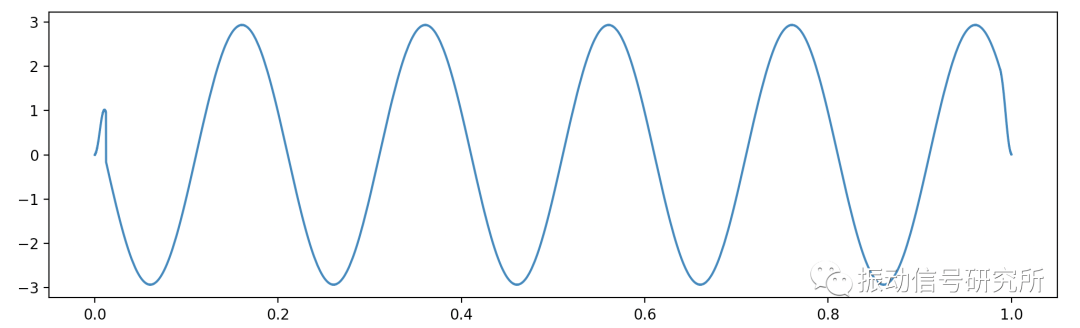
濾波的結果
這一步的運算代碼如下:
import numpy as np
from numpy import cos
import matplotlib.pyplot as plt
from filter_coeff import b
pi = np.pi
t = np.linspace(0, 1, 8192)
signal = 3 * cos(2 * pi * 5 * t + pi/3) + 7 * cos(2 * np.pi * 3000 * t + 3/8*pi)
fir_len = len(b)
res = []
for i in range(len(signal)):
print(i)
temp = 0
if i < fir_len:
data = (fir_len-i) * [0] + signal[0:i].tolist()
elif i > len(signal) - fir_len:
data = signal[i:].tolist() + (fir_len - len(signal) + i) * [0]
else:
data = signal[i:i+fir_len]
for j in range(fir_len):
temp += b[j] * data[-j-1]
res.append(temp)
plt.figure()
plt.plot(t, res)
plt.show()
-
濾波器
+關注
關注
161文章
7855瀏覽量
178597 -
低通濾波器
+關注
關注
14文章
478瀏覽量
47483 -
FIR
+關注
關注
4文章
147瀏覽量
33240 -
FFT變換
+關注
關注
2文章
10瀏覽量
8798
發布評論請先 登錄
相關推薦
DSP in FPGA:FIR濾波器(一)
高效FIR濾波器的設計與仿真-基于FPGA
用MATLAB設計FIR濾波器的方法
高階FIR正交鏡像濾波器的設計
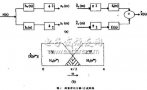
FIR濾波器的FPGA設計與實現
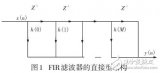
FPGA的FIR抽取濾波器設計詳細教程
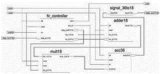
FIR濾波器與IIR濾波器到底有什么區別





 介紹一下FIR濾波器的使用
介紹一下FIR濾波器的使用










評論