積分講授為累積

非常不幸的是, 對許多學生來說, 積分僅僅限于求面積、體積以及記憶求原函數的種種法則. 許多理由表明, 若不將積分理解為累積, 那么積分教學就是失敗的. 我們指出其中三個理由。

首先, 歷史告訴我們, 累積是一個直觀的過程. 我們粗看一下歷史. 古埃及人在發現四棱臺的體積公式時幾乎肯定應用了某種形式的累加增量. 中國人在公元 5 世紀以前就掌握了求體積的卡瓦列里方法.這是微積分很明顯地跨越了文化的一個方面。

其次, 學生必定能掌握可以計算定積分或求出不定積分的軟件. 雖然許多積分技巧對它們所提供的結構方面的洞察力來說是重要的, 但只有極少數人需要在課堂以外求原函數. 更有用的是將一個累積問題轉化為定積分的能力。

最后, 學生若不能將積分理解為累積, 可能就不會認識到積分在求面積與體積以外的豐富應用. 積分是用來研究具有隨時變換的累積量的事物的工具: 走過的距離、完成的工作、賺取的利潤、生成的物資、環境惡化或改良的追蹤, 等等。

我們甚至可以通過累積來介紹積分從而開始微積分教學. 這是美國亞利桑那州的湯普森 (Thompson) 所采用的方法.他的課程基于對下述本質的洞察: 微積分是研究變化的量之間的函數關系. 一個累積必定是一個函數, 描述在每個自變量值處累積了多少. 定積分首次出現時, 必定作為一個代表上限的變量的函數。

俄克拉荷馬州的厄爾特曼開發了讓學生通過累積進入積分的一系列練習, 讓學生有機會構造對所涉及的原理的理解。

他給學生展示了美國航空航天局的一個月球車, 配上一枚電池可以工作 3 小時, 而且它在

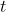
時刻的速率為

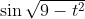
英里/時 (圖 6.1). 學生在探究它最多離開機艙多遠并仍可在那個時刻掉頭時, 就學到了估計在小時間段上的距離. 正如從圖像上容易看出的, 速率在前

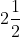
小時還多一點兒都是遞增的. 更確切地說, 它在

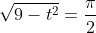
時取得最大值, 此時

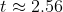
小時. 學生們會迅速領會到, 當速率遞增時, 通過取初始時刻的速率與結束時刻的速率, 即可得到所走路程的一個上下界估計. 用一個簡單的電子表格程序就足以得到合理的近似. 學生會認識到, 可以選取更短的時間區間以得到更精細的上下界, 從而得到更好的近似. 在此過程中, 可以向他們介紹求和記號, 這對他們所做的事情來說是很方便的. 此時可以向學生展示, 以行走時間為上限變量的積分是一種計量了實際累積的函數. 由于他們在第一次遇到定積分時, 定積分就以累積函數的形式出現, 因此這樣一個函數對他們來說印象深刻。

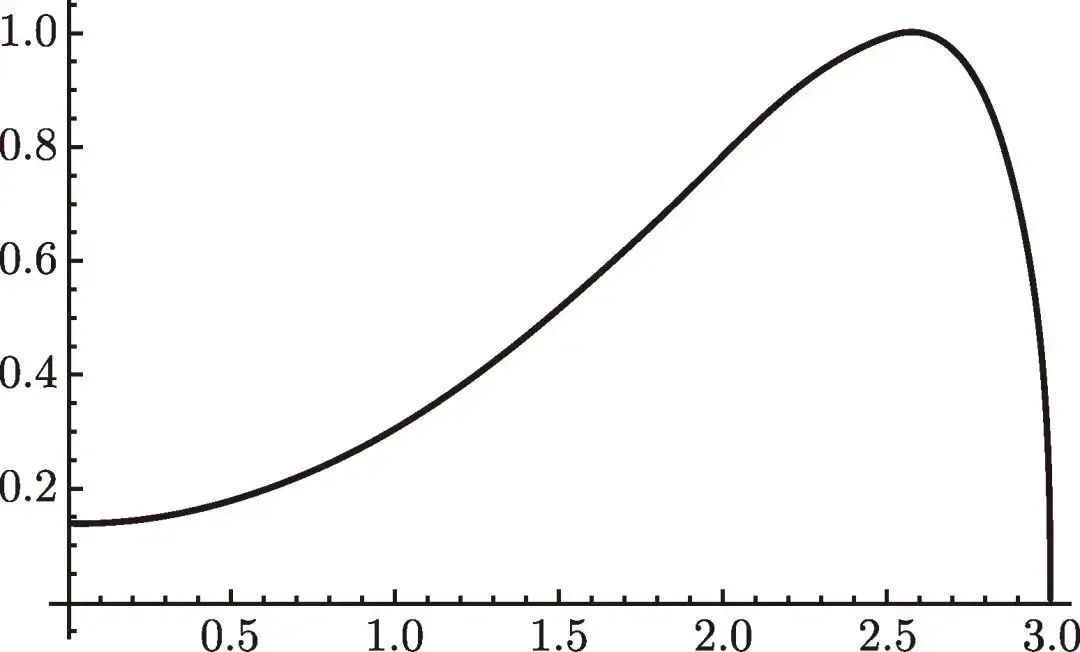
圖 6.1

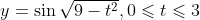
的圖像

厄爾特曼堅持讓學生每一次在選擇時間區間的同時記錄上界和下界, 也為最終引入極限播下了種子. 正如我們在第四章看到的, 現代意義下的極限是通過不等式來定義的。為了給

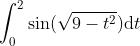
指定一個值, 就是斷言任給兩個數, 一個數比指定的數大, 另一個數比指定的數小, 我們可以選取充分小的區間段, 使得和式的值介于這兩個數之間. 這恰好就是我們所指的定積分作為黎曼和的極限的含義。

在整本書中, 我都堅持將大多數學生記得 (如果他們記得) 的這個聯系積分和微分的定理稱為積分學基本定理, 而不是簡單的微積分基本定理 (fundamental theorem of calculus). 正如我在 2.7 節腳注中所強調的, 這有歷史淵源. 更重要的是, 其背后有更深層次的教學原因. 很多學生很快就忘記了積分的極限定義. 考慮到大多數課程將重點放在了積分的技巧, 而忽略了極限定義的應用, 大多數學生認為積分與求原函數就是一回事, 這一點毫不奇怪. 造成的結果是, 原本應該處于微積分中心地位的定理被簡化為一句同義反復。

柯西第一個證明了這個定理, 他證明這個定理就是為了將積分的兩種定義聯系起來, 一個作為求和的極限, 另一個作為求原函數. 稱之為積分學基本定理不僅更準確, 而且提醒我們這個定理的本質在于將對積分的兩種不同理解聯系起來. 它可以提醒學生, 積分不僅僅是簡單的求原函數。

導數講授為變化率

我們可以質疑, 公元 1000 年左右的古印度天文學家是否從現代意義上理解了正弦函數的導數. 不過, 他們研究變化率, 致力于理解輸入的微小改變如何影響了輸出的改變. 他們已經發現, 在正弦函數的情況下, 這個變化率是一個很容易計算的量, 并且可以用來估計輸出的變化量. 比起切線的斜率來, 這是對導數的更直觀的介紹. 此外, 它為將導數最終應用到下述情形準備好了基礎, 在那些情形中, 我們只知道近似的輸入值, 還需要控制住可能的輸出值。

我們知道, 即便是微積分課堂上的學生, 理解變化率也很難, 但是他們一旦理解了變化率, 就為將導數理解為切線的斜率打好了扎實的基礎. 當我在美國瑪卡萊斯特學院教授大一新生第一學期的微積分課程時, 我的大多數學生已經多少見過微積分. 20 多年以來, 我的這門課一直以簡單評估他們對微積分的了解為開頭. 前兩個問題就是問:

在

時的瞬時變化率是多少？

在區間

上的平均變化率是多少？每個稍微了解一點兒微積分的人都能回答前一個問題. 而這些學生幾乎沒有一個答得上來后一個問題. 許多人是對在

與

時的瞬時變化率做平均. 考慮到歷史上理解瞬時速度的困難, 奇怪但真實的是, 比起平均速度來, 學生更適應瞬時速度。

我認為對此有一些解釋. 第一個解釋是, 平均變化率在微積分的先修課程中沒有得到基本的強調. 雖然它出現在每一門微積分課程的入門素材中, 但很快就被忘記了, 因為學生的注意力轉向了微分的種種技巧以及確定瞬時變化率的簡單方法. 另一個解釋是, 這個術語被稱為“平均”. 但它看起來都不像學生在小學和中學學到的任何平均. 最后, 平均變化率是一個比值。

學生很難理解導數的極限定義的重要性. 如果我們試著向學生解釋

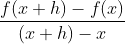
是從

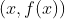
出發的一條割線的斜率, 而且當

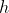
趨于 0 時, 就成為該點處切線的斜率, 我們所說的含義就在這些接踵而至的陌生概念中丟失了。

事實上, 我們可以從一個描述時刻

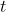
的累積量的函數出發, 并問它在

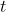
時刻的累積率是多少. 厄爾特曼讓學生估計一支箭射出 2 秒以后的速度, 假定它在

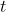
時刻的高度為 (圖 6.2)

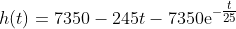
米/秒 .

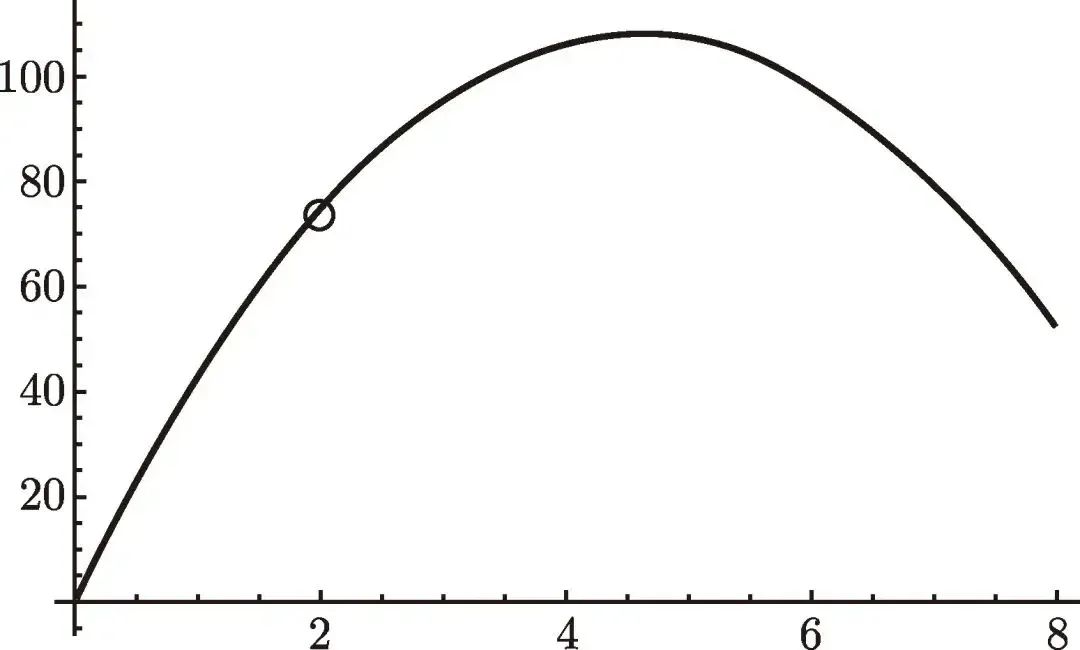
圖 6.2

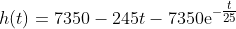
的圖像

學生們被要求估計這個速度的上界與下界, 并且誤差不超過 0.1 米/秒, 這使他們能夠求出近似速度, 并給出近似值的誤差范圍。

導數的定義對于理解如何求近似變化率是很重要的. 對于在頭一年的微積分課程里關于微分定理的證明, 導數的定義在某種程度上都是本質的. 但學生同時要對導數作為瞬時變化率有直觀的理解, 即一個物體在給定時刻運動得有多快. 這就對第二章所強調的微分的另一個重要方面 —— 微分方程 —— 提供了自然的引導。

納入納皮爾在對數方面的工作的一個原因, 就是要強調他在關聯變化率方面的工作. 事實上, 他得到了這樣的結果, 若

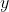
是

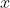
的對數, 則

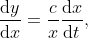
其中常數

依賴于對數的底. 不幸的是, 很少有微積分課講述了微分方程的威力與重要性. 我喜歡麥克斯韋方程組的故事, 因為它詮釋了我們如此關心微積分的一個原因, 在用數學模型來揭示這個世界的奧秘方面, 微積分具有難以預料的洞察威力. 許多革新的微積分課程, 包括最早的一些微積分改革課程, 以及我們目前在瑪卡萊斯特學院開設的課程, 都是從微分方程開始的, 并且整個課程都在強調微積分可以建立動態模型. 再一次, 軟件技術使得學生可以很容易地探究種種模型: 人口增長、流行病的傳播、捕食者與被捕食者模型. 這為圍繞微積分的學習提供了激動人心的課題. 對如何完成數值近似的分析架起了一座橋梁, 讓導數回到變化率的極限。

導數是一個豐富的概念, 帶來了眾多新的理解. 但對許多學生來說, 他們唯一的收獲就是將x^3變成3x^2, 這是何其不幸!

無窮級數講授為部分和序列

大多數情況下, 微分約化為求導, 積分約化為求原函數, 無窮級數約化為判定斂散性. 其實無窮級數是關于部分和的一種比較差勁的觀點, 因為很少有學生能記住他們曾背誦的收斂判別準則, 我非常贊同許多院校的做法, 先等到學生掌握了作為部分和的泰勒多項式, 然后再分析冪級數的收斂性.盡管很有挑戰性, 我卻樂于納入拉格朗日余項定理作為控制誤差的工具. 這也傳遞出了中值定理的實際重要性。

我還介紹了歐拉對指數函數的冪級數展開, 展示了無窮和帶來的妙趣, 我希望我的學生們能夠欣賞這個例子. 可以考慮讓學生從復利公式

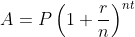
開始探究, 要求他們利用二項式定理展開, 然后探究當n增大時這個展開的性態如何, 讓他們發現這個公式與指數函數之間的關聯。

在學生的這個階段, 雖然一般的冪級數不及泰勒多項式重要, 但常數項級數與幾何級數非常重要. 在數學中, 幾何級數幾乎是無處不在的, 而且當學生學習種種收斂準則時, 幾何級數是許多收斂準則的基石。

常數項級數很重要, 這是因為, 我們對極限的現代理解源于 18 世紀為理解它們收斂之含義所付出的努力. 科學家意識到, 關鍵的問題在于, 他們能否控制住部分和與所斷言的值之間的差距. 與歷史發展的路線一致, 許多教材選取無窮求和的例子來開始極限的學習。

此外, 學生需要意識到, 當萊布尼茨斷言

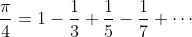
時是何其大膽. 對學生來說, 這里有個機會讓他們弄明白, 這樣一個等式的含義是什么. 討論

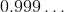
的含義自然融入該框架內。

極限講授為不等式的代數

雖然在微積分課堂上給大一的學生講授極限的

定義并要求他們掌握是不負責任的, 但這個形式化背后的思想對他們來說是可以接受的. 不論是積分、導數還是級數, 它們都是通過逼近來定義的. 極限是一個預先指定的值, 對任意的兩個界, 一個比這個給定的值大, 另一個比這個給定的值小, 一旦我們限制區間的長度 (對積分和導數而言) 或部分和的最小項數 (對無窮級數而言), 總可以使得近似在這兩個界之間。

在微積分中應用的極限的思想也許看起來很簡單, 但事實上它可以相當復雜. 對學生理解方式的探究揭示出, 學生在理解極限思想時最常用的一個比喻是被研究者稱為“坍塌”的比喻. 不論是以明確還是隱含的方式, 學生將

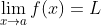
理解為, 當x越來越趨近于a時,

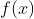
就越來越接近于L, 直到當x到達a時,

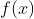
坍塌到L

對極限的大多數應用來說, 這個解釋并不太壞, 而且常常被證明富有價值, 不過它也造成了一些危險的誤導. 正如斯溫亞德 (Swinyard)曾證明的, 這是對極限的一種“以x為先導”的視角, 考察自變量的變化如何影響因變量的變化. 問題在于, 極限的真正定義是“以y為先導”的, 先圍繞y值選擇一個可容許的誤差, 然后確立存在x值的一個范圍可以保證這一點. 斯溫亞德和拉森 (Larsen)曾表明, 學生理解極限的正確定義有極大的困難, 直到他們轉換到“以y為先導”的理解。

在英國數學家戴維·托爾 (David Tall)給 22 名數學專業的大四學生提出的下述問題中, 坍塌比喻也帶來了困難。

若

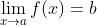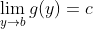且 , 是否必然有 ？

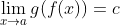即便在反復要求再次考慮答案以后, 22 名學生中仍然有 21 名堅持認為

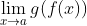
必定等于c。

正是關注“越來越接近”讓他們誤入歧途. 對

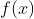
越來越接近b的理解自然引出這樣的誤解: 越來越接近b的變量y可以替換為

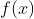
. 但如果

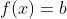
是一個常數函數, 而g在b處有極限但不連續, 即

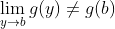
, 會發生什么呢？在這種情況下,

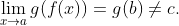
學生在理解

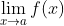
時經常忽視的一個細節是,x不能等于a, 而

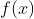
可以等于極限值. 注意, 這處于托爾的例子的核心. 當寫

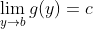
時, 我們在考慮變量y, 它是明確不等于b的. 但當我們寫

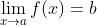
時, 并沒有排除在a附近的x滿足

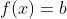
的可能性。

我們很自然會問, 為什么在定義a處的極限時, 要排除自變量等于a的情形？這是因為對于在a 處沒有定義的函數, 我們也需要考慮其極限, 特別是在導數的定義中. 當

時, 平均變化率

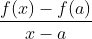
沒有定義. 我們需要極限的一個定義, 它只要考慮

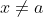
的情況。

厄爾特曼引導學生發現微分和積分原理的探究例子源于他對學生用來解釋極限的“坍塌比喻”之分析.他發現, 對許多學生來說, 近似的語言是自然而高效的. 明確了這一點后, 他研發了許多任務, 要求學生將他們的近似思想系統化, 利用不等式的代數來預先指定近似導數或積分要達到的精度. 這讓學生對這些概念有了切實的理解, 并為最終過渡到形式定義奠定了基礎。

正如厄爾特曼在 2008 年報告的,不論是微分、積分還是級數, 在每一種背景下, 學生都必須回答五個關鍵問題:

(1) 你在對什么東西做近似？

(2) 近似是什么？

(3) 誤差是什么？

(4) 誤差的界是多少？

(5) 誤差是否可以控制在任意預先指定的精度內？

如厄爾特曼所解釋的, 最后兩個問題其實是一對互逆的問題: 給定近似中所用參數的描述, 誤差的界是多少？給定誤差的界, 如何選取近似中的參數？

并非只有厄爾特曼采取了這個方法. 彼得·拉克斯 (Peter Lax) 和瑪利亞·特雷爾 (Maria Terrell) 在其《微積分及其應用》(Calculus with Application) 的開篇以不等式的論述為開端, 對極限進行了仔細的介紹。

最后, 我要稍微講一講無窮小. 近一千年來以來, 它是富有成果的洞見的源泉. 無窮小仍然具有巨大的直觀吸引力, 經常幫助科學家將累積問題轉化為定積分, 幫助他們導出微分方程. 雖然基于無窮小的微積分可以嚴格化, 但那是一個需要成熟的集合論的 20 世紀的成果. 不過完全依賴于無窮小的主要問題在于, 過渡到對極限的現代理解將變得困難得多. 考慮到學生如此容易掌握近似和不等式, 這看起來是一個更自然且富有成果的途徑。

審核編輯 ：李倩