一，邏輯門電路

我們在設計數字電路時，都希望器件的功耗低、速度快并且封裝（器件價格）便宜。但這如同所有的“神秘三角”一樣，是不可兼得的。所有的邏輯器件都是在權衡了功耗、速度和封裝之后的折衷方案：

——“神秘三角”有項目的管理三角：范圍、時間和成本；病毒三角：傳染性、毒性和適應性（新冠病毒之所以沒有滅絕人類，就是因為它受到了這“神秘三角”的約束）；等。

1. 標準封裝在制造時節省了費用，但降低了器件的靈活性；
2. 標準封裝限制了每個封裝單元內的門電路和管腳數量，迫使設計者將大的系統拆分成多個器件；

——器件之間的信號連接響應明顯比同一封裝內信號要慢，所需的功率更大；即，使得系統的性能降低，功耗增加。

3. 標準的封裝結構限定了器件所允許的最大散熱能力，如果要改進封裝的散熱能力，則需要花費額外的成本；
4. 隨著芯片制造工藝的改進，每個邏輯單元尺寸變的更小，在相同的封裝內可以集成更多的門電路數量；高密度的封裝有助于降低產品尺寸和組裝成本，但這意味著需要更大的單位面積散熱的能力；

——每個封裝所允許的最大散熱功耗限定了封裝內的門電路數量。

5. 高速器件通常消耗更大的功率，速度和功率在一定程度上可以相互對應；所以封裝的最大散熱功耗，也稱為了高速的限制因素。

——在相同制造工藝下，速度越高的器件功耗會越大。

所以對于邏輯門電路高速特性，我們主要考慮如下三個方面：

1. 功耗：分為靜態功耗和 動態功耗 ；
2. 速度：

1, 理論上：數字邏輯的設計重點是關注 邏輯門電路的傳輸延時 ；

2, 實際上：通常取決于 最小輸出轉換時間（邊沿時間） 。

——較快的轉換時間會導致回流，串擾和振鈴等與傳輸延時無關的問題倍增。

3. 封裝，對于任何高速器件封裝都會引入：管腳寄生電感、寄生電容以及散熱的問題。

二，功耗

我們想要知道一個邏輯器件的功耗，一般會查看其數據手冊上的典型電流值Icc，但這并非是器件的實際功耗，或則說在一些條件下器件的功耗會遠大于標稱的Icc電流值。舉個栗子：常用的16位驅動器74LVTH16245，如果16個輸出管腳同時快速翻轉，那么其實際功耗應該會遠超規格書中的Icc，如下圖所示。

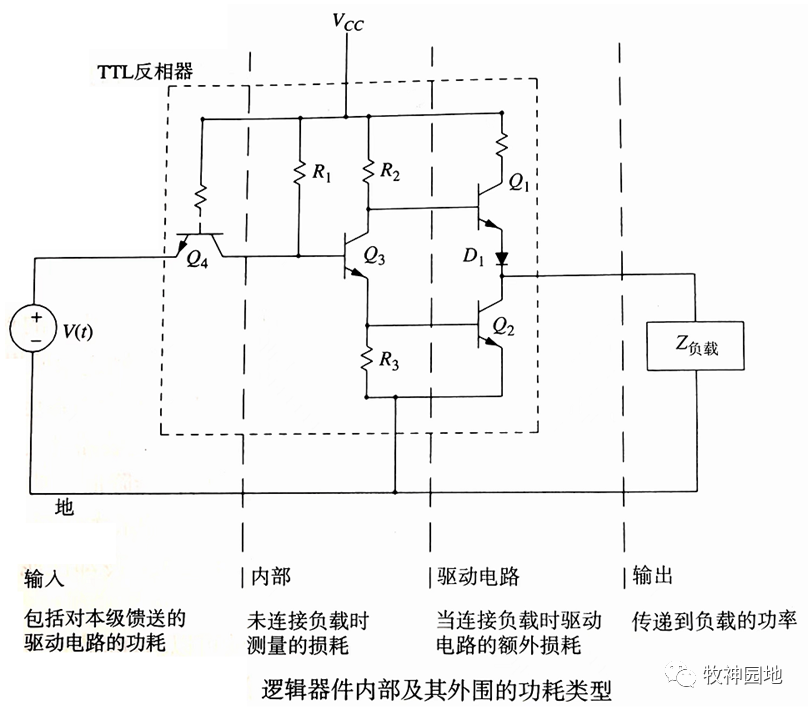
如下圖所示，為一個簡單的TTL反相器的內部邏輯結構，從功耗角度分為4部分：

——如下每一種功耗都可以進一步細分為：靜態功耗和動態功耗。

1. 輸入功耗；
2. 內部功耗；
3. 驅動電路功耗；
4. 輸出功耗。

1，靜態功耗和動態功耗

這里非常重要的概念是：靜態功耗和動態功耗。我們所有的功耗都可以將它分為這兩部分。

靜態功耗：指邏輯電路保持一個邏輯狀態時消耗的功率。靜態功耗可以由每個阻性單元兩端電壓V和電流I的乘積計算所得（P靜態 = V*I），并且求和得到總功率，這是在沒有負載情況下的靜態功耗（即數據手冊上看到的Icc標稱值）。

——需要強調的是：靜態功耗是不計負載損耗的器件自身功耗。

但實際上邏輯電路不跳變則無法傳遞信息，也就成了無用之物，我們需要器件“動”起來，那么器件就要消耗超過它正常靜態功耗之外的“額外功率”。當這個變化很有節奏時，舉個栗子：以時鐘信號頻率跳變；那么：動態功耗 = 周期頻率* 每個周期額外的功率。

——動態損耗最常見的原因：負載電容（RC充電）和偏置電流。

如下圖所示為驅動一個容性負載時的情形：

1. t1時刻電路開關A閉合（B斷開）：負載電容充電至Vcc，在電容充電時電流流過驅動電阻“R充電”，有功率消耗；
2. t2時刻電路開關B閉合（A斷開）：負載電容通過電阻“R放電”進行放電，電流流過驅動電阻，也有功率消耗；
3. t1和t2之間有一個“死區時間”（A和B都斷開）：此死區時間是為了防止電源Vcc直接通過開關短路到GND，造成器件損耗增加，甚至燒壞內部開關。

——該“死區時間”的原理同開關電源，在邏輯門電路中，其主要影響器件的功耗和電平切換速率（I/O管腳支持的最大速率）。

那么一個電壓源通過電阻R對容性負載C充電或放電時，是如何計算它的功耗呢？

1. 胖友們已經知道電容是一個儲能元件，并不會耗電，所以在容性負載充放電過程中不會耗電；

——如果有胖友還對這個問題有疑問：電容器有ESR，有寄生電阻呀等等；建議再回顧《阻容感基礎01》中的內容，另外我想說的是：我們要區分電容與電容器這兩個概念；電容是指容性，而電容器是指具體的器件，對于容性本身來說，它是不會造成電能的損耗，而造成損耗的是阻性。

2. 我們來考慮RC充/放電電路中電阻R的能量消耗，有如下兩個計算方法：

1, 直接計算電阻R在充電RC充電電路中的功耗：P = I2 * R，由于電流并非線性的，而是指數函數：(U/R)*exp(-t/τ)；所以需要用到積分公式來進行計算，具體計算如下：

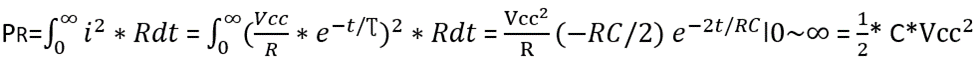
RC放電電路是充電的反向過程，同理其消耗在電阻R上的功耗也為(1/2)* CV2cc；所以充放電的總功耗為：P = CV2cc；

——指數函數的積分（面積）是1（即指數函數積分從-至x的積分值就是其本身，t 是-∞至0，那么可得積分為e?= 1），具體請參考《傳遞函數和波特圖》的“說在開頭”章節關于自然常數e的描述。

2, 將RC電路看成一個整體，同時將充電和放電看成一個整體；那么器件給R/C充電的總能量，就等于RC充電和RC放電兩個過程中總共消耗的能量；電源消耗總能量：P = VccIt = VccQ = Vcc Vcc C = C V2cc；

——電源總能量是指器件Vcc通過“R充電”給容性負載C充電，然后由容性負載C通過“R放電”釋放掉的總電能量；經過整個充電和放電過程，容性負載上并無能量儲存，所以所有的能量都被電阻所消耗，即，我們可認為Vcc釋放出來的能量都消耗在了電阻上。

3, 所以我們得到結論：對于恒壓電源充電 / 放電電路來說 ，不管串接的電阻R阻值是多少，每個充電周期消耗掉的能量是總電源能量的一半：(1/2)* CV2cc；而整個充放電周期（管腳輸出一個時鐘周期）消耗的能量是：C V2cc。

3. 如果器件管腳以f Hz頻率循環工作，那么驅動電路的功率為：f * C* V2cc。

——舉個栗子：輸出10MHz時鐘信號，負載電容為10pF，電壓為3.3V，那么驅動功率：1010?Hz1010?12F3.33.3V2 ≈ 1.110?3W = 1.1mW；這么一算單個管腳的功耗還是比較小的；但這只考慮了理想情況，后續還有跟個詳細的分析。

2，疊加偏置電流的動態功耗

如上圖TTL反相器的輸出驅動電路在H（高電平）和L（低電平）之間較低轉換，Q1和Q2交替處于導通狀態，而非兩者同時導通；這種電路配置有兩個激勵電路：一個把輸出電壓上拉到H，另一個將輸出電壓下拉到L，通常稱之為推挽輸出電路。TTL和CMOS都有推挽輸出，如下左圖為CMO推挽式輸出電路。

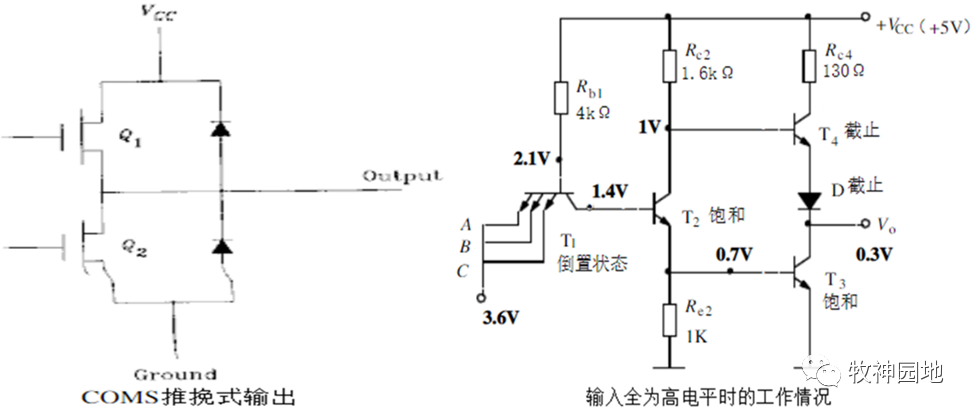
TTL推挽式輸出結構工作原理如上右圖所示，結構中各個器件的作用如下：

1. 二極管D保證了在T2和T3全飽和時，輸出電平鉗位輸出是低電平，防止T3和T4同時導通產生大的交越電流；

——所有推挽式輸出電路都需要有保護電路，防止高驅動和低驅動電路同時導通。

2. 如果輸入電平轉換很快時，每個周期都有一個交越電流并消耗一定的功耗（如下圖所示），交越電流產生的額外功耗與轉換速率成正比；

——對于一個快速的輸入轉換，重疊電流脈沖的大小和波形在每個周期都是一致的，并且每個周期消耗的能量也相同，所以這部分額外功耗與轉換速率成正比，與容性負載導致的功耗不同：交越電流產生的功耗并不隨電源電壓的平方增加。

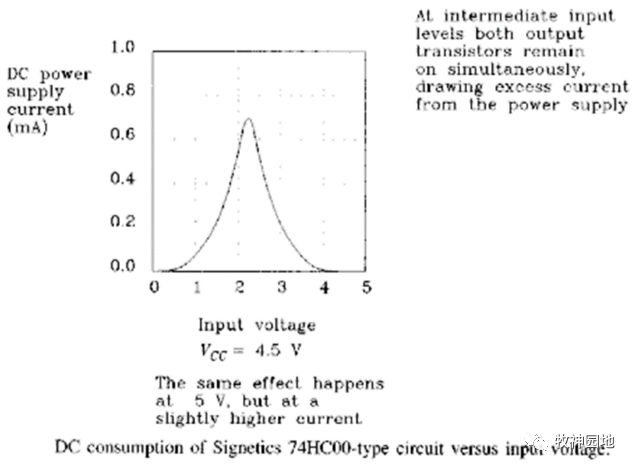
3. 減緩輸入信號邊沿，會導致交越時間延長；如上圖為門電路典型直流電源電流與輸入電壓的函數關系曲線。

——減緩輸入電壓的轉換時間往往會延長交越時間，導致T3和T4同時導通的電壓附近停留的時間會更長，所以很多器件會對輸入信號邊沿時間有要求。

4. 對于TTL電路來說，交越效應相比CMOS更顯著；如果將一個TTL反相器的輸入端與其輸出端相連，會產生自我偏置，從而進入交越范圍內，消耗大量能量。

——因此TTL電路不適合用作線性的小信號處理器（如：振蕩器），因為它們在線性工作狀態是要消耗額外的能量。

3，輸入功耗

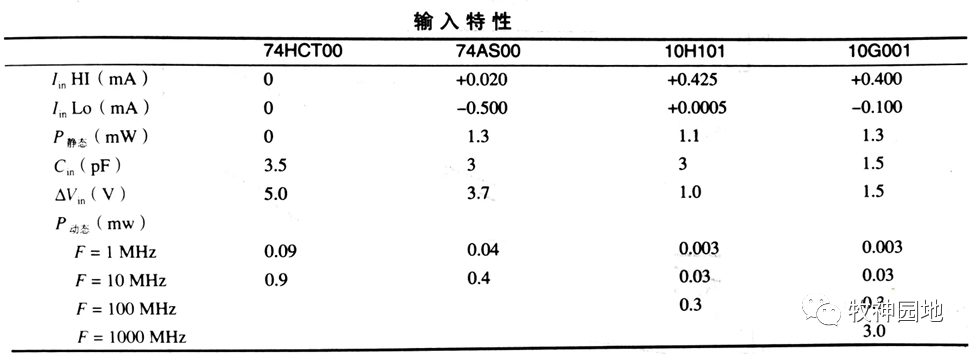
芯片的輸入功耗，來自于輸出器件，并由它來激活輸入電路。對于輸入電路的偏置和觸發來說是必需的。如下表對比了4種不同邏輯器件的靜態和動態輸入特性：

1. 靜態輸入功耗：驅動電壓和輸入電流的乘積；它包含了接收邏輯器件內部功耗和驅動器的功耗之和。
2. 動態輸入功耗：需要計算輸入電容、典型供電電壓和工作頻率代入公式：功率 = f * C*V2cc；計算出電路驅動該輸入時的總功耗。

——這些功耗相對比較小，只有較大數量扇出（Fanout）或系統要求在極低功耗運行時，才能體現其重要性。

4，內部功耗

內部功耗是指邏輯器件內部偏置電流和內部邏輯翻轉的功耗，包括靜態和動態功耗。

1. 靜態內部功耗：是指在無負載驅動、輸入端處于隨機狀態條件下的功耗，是所有輸入狀態（高/低/高阻）下的平均值；
2. 動態內部功耗：是指內部動態耗散常數“K動態”是在輸出懸空，預設輸入頻率為時測量得到總功率P總，而后計算動態功耗常數： K動態 = (P總 – P靜態)/f ；

——動態常數K動態表示周期頻率每增加1Hz將額外消耗的功率。

3. 計算任意頻率下的總功耗：總 = P靜態 + f*K動態。

——動態頻率在相對較頻率（>10MHz）時才會比較明顯。

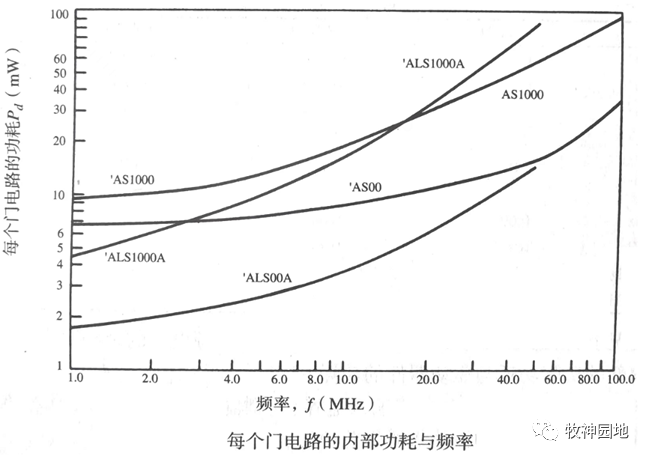
在非常寬的頻率范圍內，CMOS器件的內部功耗和周期頻率呈明顯的線性關系，這是因為CMOS電路的內部靜態功耗非常低；而TTL器件由于內部靜態功耗較大，所以直到工作頻率接近器件的最大工作頻率時才呈現出線性關系。如下圖所示為不同類型TTL邏輯器件的門電路內部功耗與工作頻率的關系曲線：

1. 在10MHz以上：動態功耗遠大于靜態功耗，總功耗曲線幾乎與頻率成正比；
2. 在1MHz以下：動態功耗小于靜態功耗，總功耗曲線相對于頻率是平坦的。

CMOS器件數據手冊用等效電容Cpd來表示內部功耗，CMOS內部功耗 = Cpd * V2 * f。可得到CMOS器件功耗的關聯因素：

1. 與管腳工作頻率和負載電容成正比；

1，器件工作頻率越來越高，是整個行業的發展方向，所以不能以降低管腳工作頻率為代價來減小器件功耗；

2，負載電容與器件封裝技術相關，器件小型化是發展趨勢，但負載電容不能無限制地減小，需要付出更多的成本代價。

2. 與I/O工作電壓的平方成正比。

——減小I/O工作電壓對功耗影響非常大（平方正比關系），是最明確可行的方案，舉個栗子：I/O電壓從5V減小至1V，那么功耗將減小至1/25；所以我們看到器件工作電壓是越來越小的趨勢。

5，驅動電路功耗

邏輯器件中的主要能量消耗在輸出驅動電路上，而驅動電路功耗由：輸出電路的結構、邏輯電平、輸出負載以及運行速度決定。我們主要考慮2種輸出結構：

1. 推挽電路輸出；
2. 射極跟隨器輸出；

5.1 推挽電路輸出

如下左圖所示為理想TTL驅動器在H（高電平）和L（低電平）狀態下的靜態功耗，對于標準TTL器件來說Q2處于飽和狀態（低電平）時的壓降VL固定在大約0.3V；在高電平H狀態下，壓降由Q1的VBE和正向偏置二極管D1鉗位（Vcc - VHI），約為1.4V。此時TTL驅動電流電路總靜態功耗平均值近似為：P靜態 = (0.3I灌+1.4I源)/2。

——此時Q1不會進入飽和狀態，因為其B極電壓不會上升到高于它C極電壓（三極管飽和狀態判斷，具體參考《三極管原基礎》相關章節）。

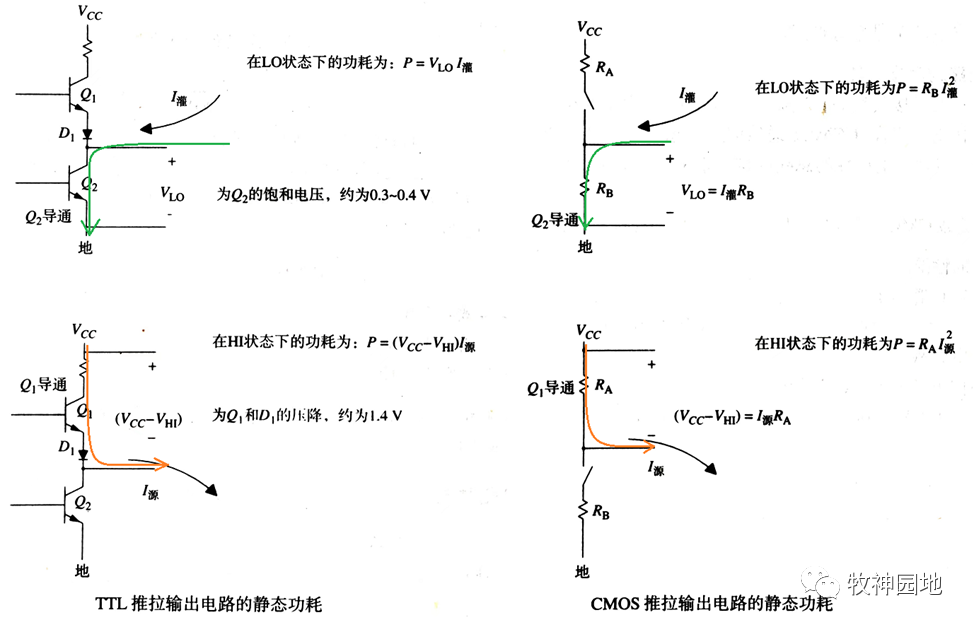
如上右圖所示為CMOS驅動器電路，MOS管的導通壓降很低，通常等效串聯了上拉和下拉電阻；所以CMOS驅動器在高電平和低電平狀態下的靜態功耗：P靜態 = (RbI2灌+RaI2源)/2。

——舉個栗子：某器件VOL（Io = 4mA），25℃時典型值為0.15V，最大值為0.33V；某器件VOH（Io = -4mA），25℃時典型值為4.32V，最大值為3.48V；那么根據R = V/I，可計算Ra的阻抗范圍是：37Ω83Ω；Rb的阻抗范圍是：45Ω165Ω。在不同電源電壓下，CMOS驅動器的輸出電阻變化很大。

推挽電路輸出負載能力，如果只按照所接負載直流輸入要求進行計算，使輸出負載能力達到它的直流最大扇出，特別是CMOS總線理論上的扇出能力是無限的；重負載的總線結構會帶來兩個問題：

1. 邊沿時間會變緩；
2. 驅動器功耗增大。

輸出總負載電容為：器件管腳寄生電容（10pf/pin）+PCB走線寄生電容（2pf/in）。舉個栗子：我們有20個負載和10in長度的PCB走線，那么總電容 = 負載電容+走線電容 = 2010pf/pin + 10in 2pf/in = 220pF；此時信號邊沿時間會變緩以及線路延遲會非常大。充電時間常數約等于驅動器輸出電阻乘以輸出負載電容，Trc = RC = 110Ω 220pF = 24ns（假設總線驅動器輸出電阻為110Ω）。

——充電時間常數是指：電容從0充電至0.63Vcc所需的時間，升至高電平90%所需時間是Trc的兩倍多：T10-90 = 2.2Trc = 53ns。

計算推挽電路動態輸出功耗：f * C* V2cc；假設最差供電電壓為5.5V，負載電容如上所述為220pF，信號線輸出頻率為10MHz，那么可得每個驅動器的功耗：1010?Hz22010?12F5.5V2 ≈ 0.067W，如果這是一個16bit的驅動器，那么同時翻轉產生的器件總功耗：P總 = 16*0.067w ≈ 1.1W。而且當上升時間緩慢時，驅動器的功耗會更高。

5.2 射極跟隨器（ECL）電路輸出

如下圖所示為ECL射極跟隨器輸出電路，該電路在HI（高電平）和LO（低電平）兩個狀態下都有電流流過。HI（高電平）和LO（低電平）輸出電壓都是相近的，這些器件一般用-5.2V電源供電，高電平VHI= -0.9V，低電平VLO = -1.7V；同時射極耦合邏輯電路需要有一個上拉電阻R，用于端接至Vt = -5.2V或中間電壓 -2.0V（戴維南匹配，具體參考《反射與阻抗匹配》），那么可得輸出電路的靜態功耗：

P靜態 = (1/2) [(Vcc-Vhi) (Vhi-Vt)+(Vcc-Vlo)*(Vol-Vt)]/R

其中，Vcc =0V，VHI= -0.9V，VLO = -1.7V, Vt = -5.2V；那么計算可得：P靜態 = 4.91/R。

同樣，如果將R下拉至-2.0V時，可以計算得到：P靜態 = 0.75/R。

那么我們可以得到：對于相同的電阻值R，使用中間電壓（-2.0V）端接時表現出明顯的功耗優勢；這是因為當電源電壓被下拉到-2.0V時，下拉電阻汲取的電流比較小（意味著低功耗）。

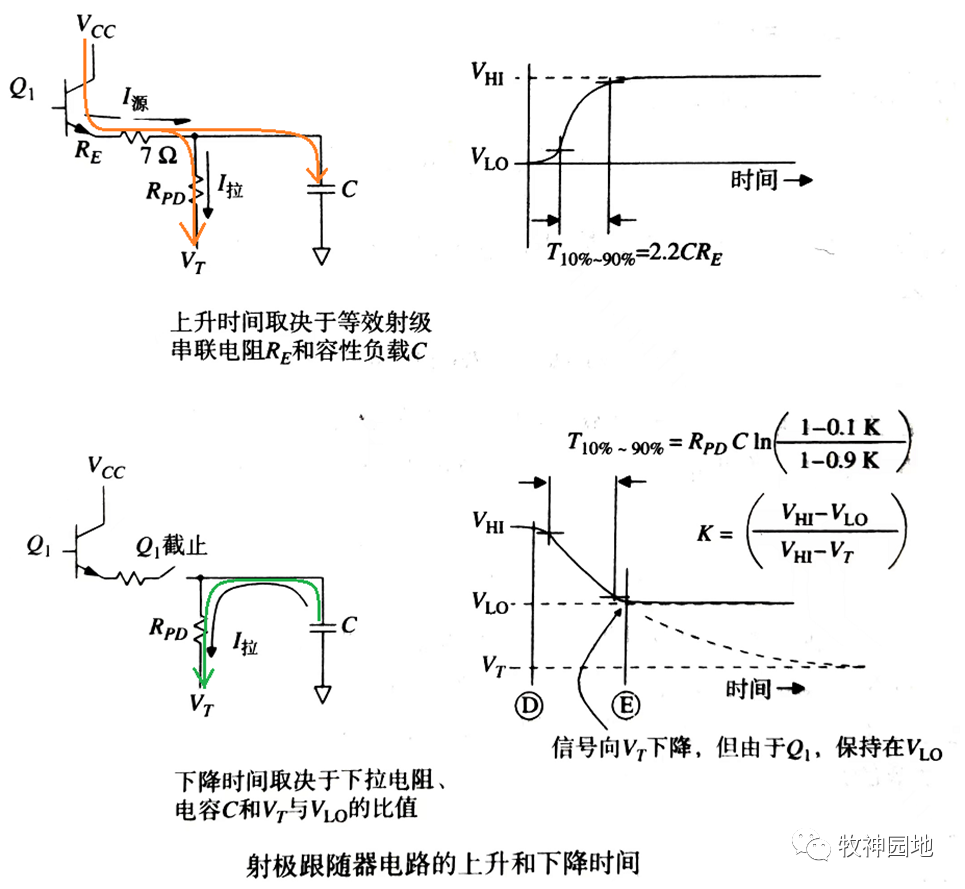
1. 如上圖所示，當晶體管Q1導通（信號上升沿），電流從晶體管輸出流向下拉電阻Rpd和容性負載；由于Rpd相對于Re更大，Rpd的下拉電流相對于Re輸出的I源電流可以忽略不計，所以輸出電壓上升時間不受下拉電流的影響；

——上圖中給出Re = 7Ω，當給容性負載C充電時，其充電時間常數為：Trc = Re* C；而充電至90%所需的時間為T10-90 = 2.2*Trc。

2. 當晶體管Q1截止（信號下降沿），從而不再有電流流過發射極；只有容性負載C通過下拉電阻Rpd放電：下降時間與電容C放電的速度成正比，功耗與靜態下拉電流成正比；此時需要有一個大電流迅速地將電容C放電；

——如果Q1完全截止（忽略其漏電流），從90%-10%的下降時間為：T90-10 = RpdCln[(1-0.1K)/(1-0.9K)]；其中常數K = (Vhi-Vlo)/(Vhi-Vi)；如上面栗子參數（Vt = -5.2V），可計算K = 0.186， T90-10 = 0.164RpdC。若Vt = -2.0V，那么計算K = 0.727，T90-10 = 0.987RpdC。

3. 當Vt = -2.0V時雖然功耗相對較小，但是邊沿時間會更長，為了達到相同的相同時間，必須要求所采用的下拉電阻相比于Vt = -5.2V電阻的阻值更小，而一旦選擇了較小的電阻，其兩種匹配方式的功耗數也大致相等。

——同時考慮其它方面：1，采用Vt = -5.2V不需要引入單獨的新電源；2，采用Vt = -2.0V時下拉電阻范圍在50100Ω，正好可以作為線路的終端匹配（阻抗匹配），而Vt = -5.2V時端接電阻在330680Ω，不適合做終端匹配（關于終端匹配相關知識參考：《反射與阻抗匹配》章節內容）。

4. ECL輸出電路相對于推挽輸出電路的好處是：

1, 由于電壓擺幅小，所以電路動態功耗非常小（下拉電阻產生的損耗）；

2, 沒有推挽輸出電路的高低電平切換“死區時間”，切換的速率更快，且無額外損耗。