在數字信號處理領域中，數字濾波器占有非常重要的地位。根據其計算方式可以分為FIR(有限脈沖響應)濾波器，和IIR(無限脈沖響應)濾波器兩種。

FIR濾波器根據如下公式進行計算：

y[m] = b[0]x[m] + b[1]x[m-1] + …. + b[p]x[m-p]

IIR濾波器：

y[m] = b[0]x[m] + b[1]x[m-1] + …. + b[p]x[m-p]

-a[1]y[m-1] – a2y[m-2]- … - a[Q]y[m-Q]

FIR濾波器:時刻m的輸出y[m]由時刻m的輸入x[m]以及之前的輸入x[m-1] ... x[m-P]和濾波器的系數b[0] ... b[P]求乘積和.

IIR濾波器再減去之前的輸出y[m-1] ... y[m-Q]和系數a[1] ... a[m-Q]的乘積和.

FIR濾波器是IIR濾波器的一種特殊情況.

濾波器的作用：改變信號頻譜，實現頻域濾波。

低通濾波器參數特征：

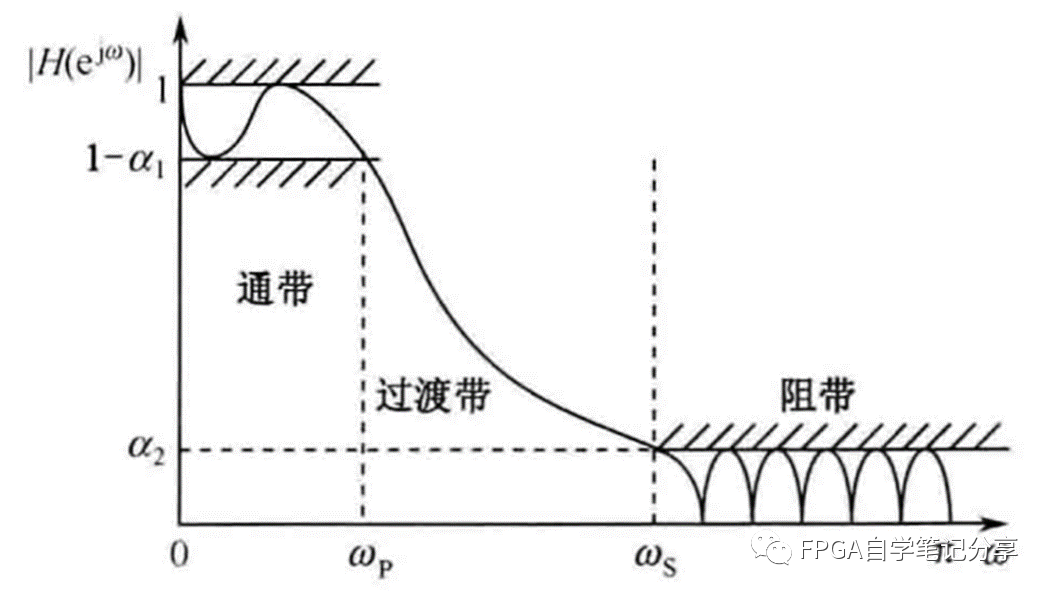
比如，設計一個歸一化為0.2通帶的低通濾波器，其頻譜響應為：

生成一個隨機信號將其作為輸入經過上述濾波器，結果如下，藍線是隨機信號的頻譜，橙線為經過濾波器后的頻譜。

再比如一個雙音信號，經過該濾波器，輸入信號頻譜：

經過濾波器濾波后的頻譜：

數字濾波器的設計，最常用的是MATLAB的 filterDesigner工具根據需求直接配置參數，即可生成濾波器系數，同時給出濾波器的頻譜響應，使用特別方便：

使用python的話可以用scipy庫的signal.remez函數：

import scipy.signal as signal
signal.remez(numtaps, bands, desired,
weight=None, Hz=1, type='bandpass', maxiter=25, grid_density=16)

其中：

numtaps : 所設計的FIR濾波器的長度

bands ：一個遞增序列，它包括頻率響應中的所有頻帶的邊界，其值在0到Hz/2之間，如果參數Hz為缺省值1的話，那么可以把它當作是以取樣頻率正規化的頻率

desired : 長度為bands的一半的增益序列，它給出頻率響應在bands中的每個頻帶的增益值

weight : 長度和desired一樣的權重序列，它給出desired中的每個增益所占的權重，即給出desired中的每個增益的重要性，值越大表示其越重要

type : 'bandpass'或者'differentiator'

比如設計一個歸一化為0.1的低通濾波器，截止頻率0.11，系數長度701的濾波器：

len_h=701
bands = np.array([0., 0.1, .11, .5])
h = signal.remez(len_h, bands, [1,0], [100,1])

濾波器的頻譜響應為：