FFT的算法推導主要用到旋轉因子的周期性、對稱性和可約性：

基2FFT的頻域抽取法，將x(n)按照n的自然順序劃分為前后兩個部分：

所以當K為偶數時，前后兩部分相加。當k為奇數時相減。將頻域X(K)劃分為奇偶兩個序列，N點DFT就被分解為兩個N/2點的DFT：

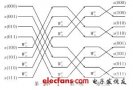
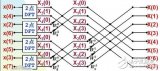
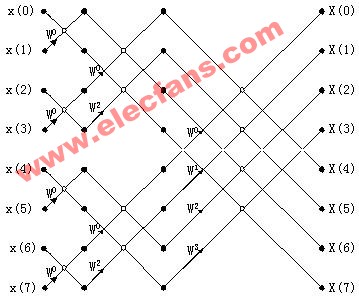
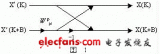
可以得到蝶形圖如下：

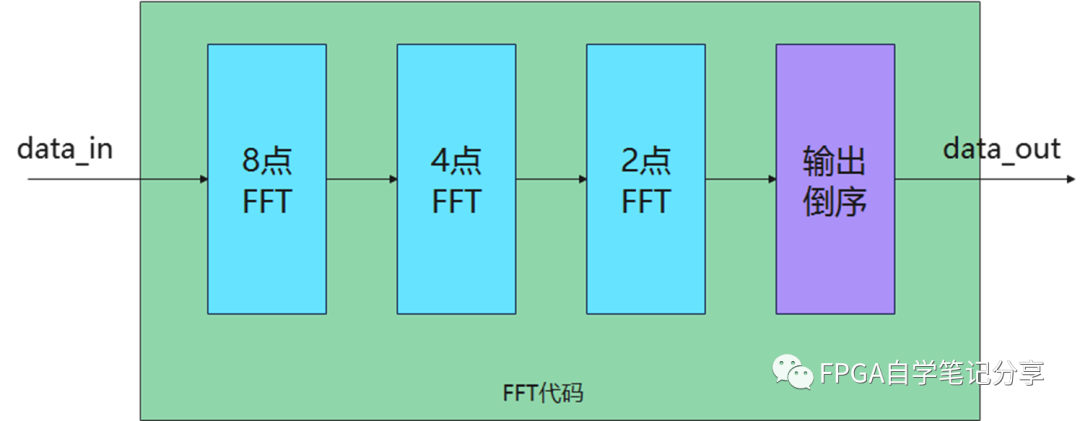
進而可以得到基2FFT頻域抽取代碼的實現方法：

隨后是數據倒換，如下圖：

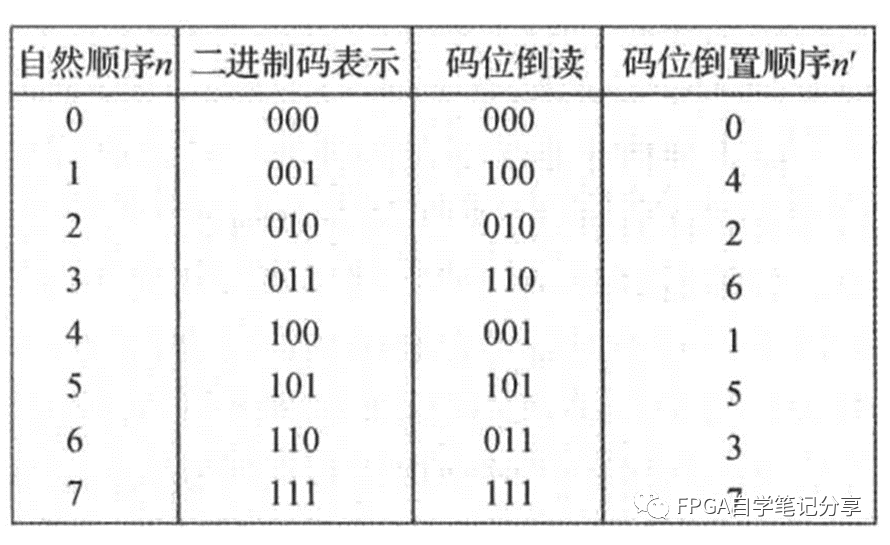
可以看到基2FFT頻域抽取后的輸出位置排序就是自然數二進制碼按位倒讀的值。

根據推導結果我們編寫python實現代碼：

首先根據FFT的點數計算需要迭代的次數，根據迭代次數例化一個loop_num+1*N的數組一共來存儲輸入及中間迭代的結果，同時將輸入X送入第一行作為輸入：

import numpy as np
import matplotlib.pyplot as plt


#頻域抽取的基2FFT
loop_num= int(np.log2(N))
data=np.zeros((loop_num+1,N),dtype=np.complex)
data[0]=x

隨后開始FFT的迭代，循環變量i一共來表征迭代的次數；循環變量p用來表征每次循環將將數據換分為幾塊；循環變量j用來進行蝶形運算。通過循環完成FFT的迭代及運算，代碼如下：

for i in range(loop_num):
    k=i+1
    for p in range(2**i):
        for j in range(N//(2**k)):
            data[i+1][j           +p*(N//(2**i))] =  data[i,j+p*(N//(2**i))] + data[i,j+N//(2**k) +p*(N//(2**i))]
            data[i+1][j+N//(2**k) +p*(N//(2**i))] = (data[i,j+p*(N//(2**i))] - data[i,j+N//(2**k) +p*(N//(2**i))])*np.e**(-1j*2*j*np.pi*(2**i)/N)

最終將FFT蝶形運算的結果進行輸出倒序，定義rev2(k,N)遞歸函數達到按bit翻轉的目的，最終輸出FFT結果為fft_out：

def rev2(k,N):
    if (k==0):
        return (0)
    else:
        return(((rev2(k//2,N)//2)+(k%2)*(N//2)))


#輸出倒序
fft_out = np.ones_like(data[0,:])
for k  in range (N):
    fft_out[rev2(k,N)] = data[loop_num,k]

最后為了驗證代碼正確性，直接調用python的FFT庫函數得到xf為庫函數的結果，與fft_out相減并畫圖，觀察誤差。

xf = np.fft.fft(x)
plt.plot(abs(xf))
plt.plot(abs(fft_out-xf))

輸入1024點的任意復數：

x = [int(np.round(np.sin(i)*1024))+int(np.round(np.cos(i)*1024))*1j for i in n]

波形如下：

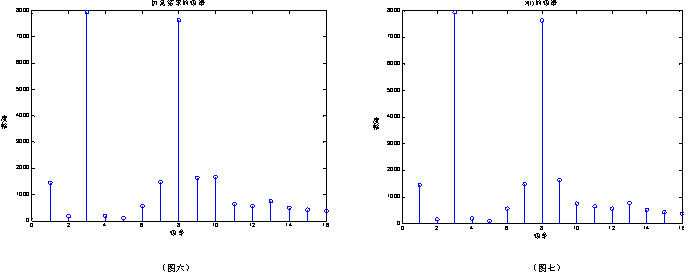
運行python算法得到結果如下，圖中藍線是FFT計算的結果，橙線是FFT庫函數計算結果與fft_out相減的差，差值為0，認為我們的迭代算法正確。