在3.1 節中,我們介紹了線性回歸,在3.4 節中從頭開始實現 ,并在3.5 節中再次使用深度學習框架的高級 API來完成繁重的工作。
回歸是我們想回答多少的時候伸手去拿的錘子? 或者有多少?問題。如果你想預測房子的售價(價格),或者一支棒球隊可能獲勝的次數,或者病人出院前住院的天數,那么你可能是尋找回歸模型。然而,即使在回歸模型中,也存在重要的區別。例如,房屋的價格永遠不會是負數,并且變化可能通常與其基準價格有關。因此,對價格的對數進行回歸可能更有效。同樣,患者住院的天數是 離散的非負數隨機變量。因此,最小均方可能也不是理想的方法。這種時間-事件建模伴隨著許多其他并發癥,這些并發癥在稱為生存建模的專門子領域中處理。
這里的重點不是要讓你不知所措,而只是讓你知道,除了簡單地最小化平方誤差之外,還有很多東西需要估計。更廣泛地說,監督學習比回歸要多得多。在這一節中,我們重點關注分類問題,我們擱置了多少?問題,而是關注哪個類別?問題。
這封電子郵件屬于垃圾郵件文件夾還是收件箱?
該客戶是否更有可能注冊或不注冊訂閱服務?
這個圖像描繪的是驢、狗、貓還是公雞?
阿斯頓接下來最有可能看哪部電影?
您接下來要閱讀本書的哪一部分?
通俗地說,機器學習從業者重載了單詞 分類來描述兩個細微不同的問題:(i)那些我們只對將示例硬分配給類別(類)感興趣的問題;(ii) 那些我們希望進行軟分配的地方,即評估每個類別適用的概率。這種區別往往會變得模糊,部分原因是,即使我們只關心硬分配,我們仍然經常使用進行軟分配的模型。
更重要的是,在某些情況下,不止一個標簽可能是真實的。例如,一篇新聞文章可能同時涵蓋娛樂、商業和太空飛行等主題,但不會涵蓋醫學或體育主題。因此,將其單獨歸入上述類別之一并不是很有用。這個問題通常被稱為多標簽分類。參見Tsoumakas 和 Katakis ( 2007 )的概述和 Huang等人。( 2015 )用于標記圖像時的有效算法。
4.1.1. 分類
讓我們先從一個簡單的圖像分類問題開始。這里,每個輸入包含一個2×2灰度圖像。我們可以用一個標量表示每個像素值,給我們四個特征x1,x2,x3,x4. 此外,假設每個圖像屬于類別“貓”、“雞”和“狗”中的一個。
接下來,我們必須選擇如何表示標簽。我們有兩個明顯的選擇。也許最自然的沖動是選擇 y∈{1,2,3},其中整數代表 {dog,cat,chicken}分別。這是在計算機上存儲此類信息的好方法。如果類別之間有一些自然順序,比如說我們是否試圖預測 {baby,toddler,adolescent,young adult,adult,geriatric},那么將其轉換為有序回歸問題并以這種格式保留標簽甚至可能是有意義的。參見 Moon等人。( 2010 )概述了不同類型的排名損失函數和Beutel等人。( 2014 ) 用于解決具有多個模式的響應的貝葉斯方法。
一般而言,分類問題并不伴隨著類別之間的自然排序。幸運的是,統計學家很久以前就發明了一種表示分類數據的簡單方法:one-hot encoding。one-hot 編碼是一個向量,其分量與我們的類別一樣多。對應于特定實例類別的組件設置為 1,所有其他組件設置為 0。在我們的例子中,標簽y 將是一個三維向量,具有(1,0,0) 對應“貓”,(0,1,0)到“雞”,和 (0,0,1)對“狗”:
(4.1.1)y∈{(1,0,0),(0,1,0),(0,0,1)}.
4.1.1.1. 線性模型
為了估計與所有可能類別相關的條件概率,我們需要一個具有多個輸出的模型,每個類別一個。為了解決線性模型的分類問題,我們需要與輸出一樣多的仿射函數。嚴格來說,我們只需要少一個,因為最后一類必須是 1和其他類別的總和,但出于對稱的原因,我們使用了稍微冗余的參數化。每個輸出對應于它自己的仿射函數。在我們的例子中,由于我們有 4 個特征和 3 個可能的輸出類別,我們需要 12 個標量來表示權重(w帶下標)和 3 個標量來表示偏差(b帶下標)。這產生:
(4.1.2)o1=x1w11+x2w12+x3w13+x4w14+b1,o2=x1w21+x2w22+x3w23+x4w24+b2,o3=x1w31+x2w32+x3w33+x4w34+b3.
對應的神經網絡圖如圖4.1.1所示 。就像在線性回歸中一樣,我們使用單層神經網絡。并且由于每個輸出的計算, o1,o2, 和o3, 取決于所有輸入,x1, x2,x3, 和x4,輸出層也可以描述為全連接層。
圖 4.1.1 Softmax 回歸是一個單層神經網絡。
為了更簡潔的表示法,我們使用向量和矩陣: o=Wx+b更適合數學和代碼。請注意,我們已將所有權重收集到一個3×4矩陣和所有偏差 b∈R3在一個向量中。
4.1.1.2。Softmax
假設有一個合適的損失函數,我們可以直接嘗試最小化兩者之間的差異o和標簽 y. 雖然事實證明,將分類處理為向量值回歸問題的效果出奇地好,但它仍然缺乏以下方面:
無法保證輸出oi總結為 1以我們期望概率表現的方式。
無法保證輸出oi甚至是非負的,即使它們的輸出總和為1,或者他們不超過1.
這兩個方面都使估計問題難以解決,并且解決方案對異常值非常脆弱。例如,如果我們假設臥室數量與某人購買房屋的可能性之間存在正線性相關性,則概率可能超過 1買豪宅的時候!因此,我們需要一種機制來“壓縮”輸出。
我們可以通過多種方式來實現這一目標。例如,我們可以假設輸出o是損壞的版本y,其中通過添加噪聲發生損壞?從正態分布中提取。換句話說,y=o+?, 在哪里 ?i~N(0,σ2). 這就是所謂的 probit 模型,首先由Fechner ( 1860 )提出。雖然很吸引人,但與 softmax 相比,它的效果并不好,也不會導致特別好的優化問題。
實現此目標(并確保非負性)的另一種方法是使用指數函數P(y=i)∝exp?oi. 這確實滿足了條件類概率隨著增加而增加的要求oi,它是單調的,所有概率都是非負的。然后我們可以轉換這些值,使它們加起來1通過將每個除以它們的總和。這個過程稱為規范化。將這兩個部分放在一起可以得到softmax函數:
(4.1.3)y^=softmax(o)wherey^i=exp?(oi)∑jexp?(oj).
注意最大坐標o對應于最有可能的類別y^. 此外,因為 softmax 操作保留了其參數之間的順序,我們不需要計算 softmax 來確定哪個類別被分配了最高概率。
(4.1.4)argmaxjy^j=argmaxjoj.
softmax 的想法可以追溯到 Gibbs,他改編了物理學的想法( Gibbs, 1902 )。追溯到更早以前,現代熱力學之父玻爾茲曼就使用這個技巧來模擬氣體分子中的能量狀態分布。特別是,他發現熱力學系綜中能量狀態的普遍存在,例如氣體中的分子,與exp?(?E/kT). 這里, E是一種狀態的能量,T是溫度,并且 k是玻爾茲曼常數。當統計學家談論增加或降低統計系統的“溫度”時,他們指的是變化T為了有利于較低或較高的能量狀態。按照吉布斯的想法,能量等同于錯誤。基于能量的模型( Ranzato et al. , 2007 )在描述深度學習中的問題時使用了這種觀點。
4.1.1.3. 矢量化
為了提高計算效率,我們將計算向量化為小批量數據。假設我們得到了一個小批量 X∈Rn×d的n維度示例(輸入數量)d. 此外,假設我們有q輸出中的類別。那么權重滿足 W∈Rd×q偏差滿足 b∈R1×q.
(4.1.5)O=XW+b,Y^=softmax(O).
這將主導操作加速為矩陣矩陣乘積 XW. 此外,由于每一行 X表示一個數據示例,softmax 操作本身可以按行計算:對于每一行O,對所有條目取冪,然后用總和對它們進行歸一化。但是請注意,必須注意避免對大數取冪和取對數,因為這會導致數值溢出或下溢。深度學習框架會自動處理這個問題。
4.1.2. 損失函數
現在我們有了來自特征的映射x概率y^,我們需要一種方法來優化此映射的準確性。我們將依賴最大似然估計,這與我們在第 3.1.3 節中為均方誤差損失提供概率論證時遇到的概念完全相同 。
4.1.2.1. 對數似然
softmax 函數給了我們一個向量y^,我們可以將其解釋為每個類的(估計的)條件概率,給定任何輸入x, 例如y^1= P(y=cat∣x). 在下文中,我們假設對于具有特征的數據集X標簽 Y使用單熱編碼標簽向量表示。給定以下特征,我們可以根據我們的模型檢查實際類別的可能性,從而將估計值與現實進行比較:
(4.1.6)P(Y∣X)=∏i=1nP(y(i)∣x(i)).
我們被允許使用因式分解,因為我們假設每個標簽都是獨立于其各自的分布繪制的 P(y∣x(i)). 由于最大化項的乘積很尷尬,我們取負對數來獲得最小化負對數似然的等價問題:
(4.1.7)?log?P(Y∣X)=∑i=1n?log?P(y(i)∣x(i))=∑i=1nl(y(i),y^(i)),
任何一對標簽在哪里y和模型預測 y^超過q類,損失函數 l是
(4.1.8)l(y,y^)=?∑j=1qyjlog?y^j.
由于稍后解釋的原因, (4.1.8)中的損失函數通常稱為交叉熵損失。自從y是長度的單熱向量q,其所有坐標的總和j除了一個任期外,所有的人都消失了。注意損失l(y,y^)從下面被限制0每當y^是一個概率向量:沒有一個條目大于1, 因此它們的負對數不能低于0; l(y,y^)=0僅當我們確定地預測實際標簽時。對于任何有限的權重設置,這永遠不會發生,因為將 softmax 輸出朝向1 需要采取相應的輸入oi到無窮大(或所有其他輸出oj為了j≠i到負無窮大)。即使我們的模型可以分配一個輸出概率0,分配如此高的置信度時出現的任何錯誤都會導致無限損失(?log?0=∞).
4.1.2.2. Softmax 和交叉熵損失
由于 softmax 函數和相應的交叉熵損失非常普遍,因此有必要更好地了解它們的計算方式。將(4.1.3)代入(4.1.8)中損失的定義并使用我們獲得的 softmax 的定義:
(4.1.9)l(y,y^)=?∑j=1qyjlog?exp?(oj)∑k=1qexp?(ok)=∑j=1qyjlog?∑k=1qexp?(ok)?∑j=1qyjoj=log?∑k=1qexp?(ok)?∑j=1qyjoj.
為了更好地理解正在發生的事情,請考慮關于任何 logit 的導數oj. 我們得到
(4.1.10)?ojl(y,y^)=exp?(oj)∑k=1qexp?(ok)?yj=softmax(o)j?yj.
換句話說,導數是我們的模型分配的概率(由 softmax 操作表示)與實際發生的概率(由 one-hot 標簽向量中的元素表示)之間的差異。從這個意義上講,它與我們在回歸中看到的非常相似,其中梯度是觀察值之間的差異y并估計y^. 這不是巧合。在任何指數族模型中,對數似然的梯度恰好由此項給出。這個事實使得計算梯度在實踐中變得容易。
現在考慮這樣一種情況,我們不僅觀察到單個結果,而且觀察到結果的整個分布。我們可以對標簽使用與之前相同的表示y. 唯一的區別是,而不是只包含二進制條目的向量,比如說 (0,0,1),我們現在有一個通用的概率向量,比如說 (0.1,0.2,0.7). 我們之前用來定義損失的數學l在(4.1.8)中仍然可以正常工作,只是解釋稍微更籠統。它是標簽分布的損失的預期值。這種損失稱為交叉熵損失,它是分類問題中最常用的損失之一。我們可以通過介紹信息論的基礎知識來揭開這個名字的神秘面紗。簡而言之,它測量對我們看到的內容進行編碼的位數y 相對于我們預測應該發生的事情y^. 我們在下面提供了一個非常基本的解釋。有關信息論的更多詳細信息,請參閱Cover 和 Thomas ( 1999 )或 MacKay 和 Mac Kay ( 2003 )。
4.1.3. 信息論基礎
許多深度學習論文使用信息論中的直覺和術語。為了理解它們,我們需要一些共同語言。這是一本生存指南。信息論處理編碼、解碼、傳輸和操作信息(也稱為數據)的問題。
4.1.3.1. 熵
信息論的中心思想是量化數據中包含的信息量。這限制了我們壓縮數據的能力。對于分配P它的熵定義為:
(4.1.11)H[P]=∑j?P(j)log?P(j).
信息論的基本定理之一指出,為了對從分布中隨機抽取的數據進行編碼P,我們至少需要H[P]“nats”對其進行編碼(香農,1948 年)。如果您想知道“nat”是什么,它相當于位,但是當使用帶有 base 的代碼時e而不是基數為 2 的一個。因此,一個 nat 是1log?(2)≈1.44少量。
4.1.3.2. 驚喜
您可能想知道壓縮與預測有什么關系。想象一下,我們有一個要壓縮的數據流。如果我們總是很容易預測下一個標記,那么這個數據就很容易壓縮。舉一個極端的例子,流中的每個標記總是取相同的值。那是一個非常無聊的數據流!不僅無聊,而且很容易預測。因為它們總是相同的,所以我們不必傳輸任何信息來傳達流的內容。易于預測,易于壓縮。
然而,如果我們不能完美地預測每一件事,那么我們有時可能會感到驚訝。當我們分配一個較低概率的事件時,我們的驚喜更大。克勞德·香農決定 log?1P(j)=?log?P(j)量化一個人 在觀察事件時的驚訝程度j賦予它一個(主觀)概率P(j). (4.1.11)中定義的熵 是當分配真正匹配數據生成過程的正確概率時的預期意外。
4.1.3.3. 重溫交叉熵
因此,如果熵是知道真實概率的人所經歷的驚奇程度,那么您可能想知道,什么是交叉熵?交叉熵來自 P 到 Q, 表示H(P,Q), 是具有主觀概率的觀察者的預期驚喜Q在看到實際根據概率生成的數據時P. 這是由 H(P,Q)=def∑j?P(j)log?Q(j). 當達到最低可能的交叉熵時P=Q. 在這種情況下,交叉熵來自P到Q是 H(P,P)=H(P).
簡而言之,我們可以通過兩種方式來考慮交叉熵分類目標:(i)最大化觀察數據的可能性;(ii) 最小化傳達標簽所需的意外(以及位數)。
4.1.4. 總結與討論
在本節中,我們遇到了第一個非平凡的損失函數,使我們能夠優化離散輸出空間。其設計的關鍵是我們采用了概率方法,將離散類別視為從概率分布中抽取的實例。作為副作用,我們遇到了 softmax,這是一種方便的激活函數,可將普通神經網絡層的輸出轉換為有效的離散概率分布。我們看到交叉熵損失的導數與 softmax 結合時的行為與平方誤差的導數非常相似,即取預期行為與其預測之間的差異。而且,雖然我們只能觸及它的表面,但我們遇到了與統計物理學和信息論的令人興奮的聯系。
雖然這足以讓您上路,并希望足以激發您的胃口,但我們幾乎沒有深入探討。除其他外,我們跳過了計算方面的考慮。具體來說,對于任何具有d輸入和q輸出,參數化和計算成本是O(dq),這在實踐中可能高得令人望而卻步。幸運的是,這種改造成本d輸入到q可以通過近似和壓縮來減少輸出。例如 Deep Fried Convnets ( Yang et al. , 2015 )使用排列、傅里葉變換和縮放的組合來將成本從二次降低到對數線性。類似的技術適用于更高級的結構矩陣近似(Sindhwani等人,2015 年)。最后,我們可以使用類似四元數的分解來降低成本 O(dqn),同樣,如果我們愿意根據壓縮因子 為計算和存儲成本犧牲少量準確性 (Zhang等人,2021 年)n. 這是一個活躍的研究領域。具有挑戰性的是,我們不一定要爭取最緊湊的表示或最少數量的浮點運算,而是要尋求可以在現代 GPU 上最有效地執行的解決方案。
4.1.5. 練習
我們可以更深入地探索指數族和 softmax 之間的聯系。
計算交叉熵損失的二階導數 l(y,y^)對于 softmax。
計算由給出的分布的方差 softmax(o)并證明它與上面計算的二階導數相匹配。
假設我們有三個以等概率出現的類,即概率向量是 (13,13,13).
如果我們嘗試為它設計二進制代碼,會出現什么問題?
你能設計出更好的代碼嗎?提示:如果我們嘗試對兩個獨立的觀察結果進行編碼,會發生什么情況?如果我們編碼怎么辦n 共同觀察?
在對通過物理線路傳輸的信號進行編碼時,工程師并不總是使用二進制代碼。例如, PAM-3使用三個信號電平{?1,0,1}而不是兩個級別 {0,1}. 傳遞范圍內的整數需要多少個三元單位{0,…,7}?為什么這在電子學方面可能是一個更好的主意?
Bradley -Terry 模型 使用邏輯模型來捕捉偏好。為了讓用戶在蘋果和橙子之間做出選擇,一個假設分數 oapple和oorange. 我們的要求是得分越大,選擇相關項目的可能性就越大,得分最高的項目最有可能被選中 (Bradley 和 Terry,1952 年)。
證明softmax滿足這個要求。
如果您希望允許默認選項既不選擇蘋果也不選擇橙子,會發生什么情況?提示:現在用戶有 3 個選擇。
Softmax 的名稱來源于以下映射: RealSoftMax(a,b)=log?(exp?(a)+exp?(b)).
證明 RealSoftMax(a,b)>max(a,b).
你能使這兩個函數之間的差異有多小?提示:不失一般性,您可以設置b=0和 a≥b.
證明這適用于 λ?1RealSoftMax(λa,λb), 前提是λ>0.
表明對于λ→∞我們有 λ?1RealSoftMax(λa,λb)→max(a,b).
軟敏是什么樣子的?
將其擴展到兩個以上的數字。
功能 g(x)=deflog?∑iexp?xi 有時也稱為對數分區函數。
證明函數是凸的。提示:為此,使用一階導數等于 softmax 函數的概率這一事實,并證明二階導數是方差。
顯示g是平移不變的,即 g(x+b)=g(x).
如果某些坐標會發生什么xi很大嗎?如果它們都非常小會怎樣?
證明如果我們選擇b=maxixi我們最終得到了一個數值穩定的實現。
假設我們有一些概率分布P. 假設我們選擇另一個分布Q和 Q(i)∝P(i)α為了α>0.
選擇哪個α對應溫度翻倍?哪個選擇對應減半?
如果我們讓溫度收斂到0?
如果我們讓溫度收斂到∞?
Discussions
-
pytorch
+關注
關注
2文章
808瀏覽量
13202 -
Softmax
+關注
關注
0文章
9瀏覽量
2506
發布評論請先 登錄
相關推薦
OneFlow Softmax算子源碼解讀之WarpSoftmax
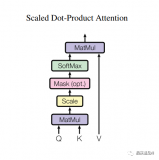
OneFlow Softmax算子源碼解讀之BlockSoftmax
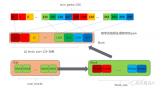
基于Softmax回歸的通信輻射源特征分類識別方法
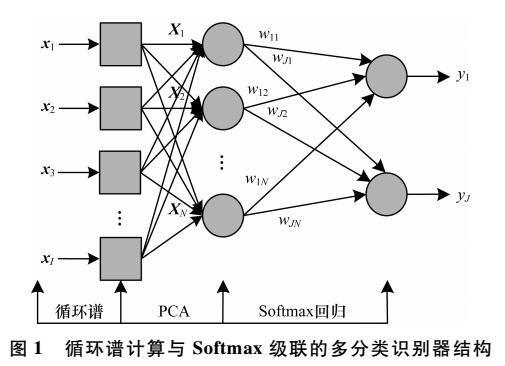
機器學習的Softmax定義和優點
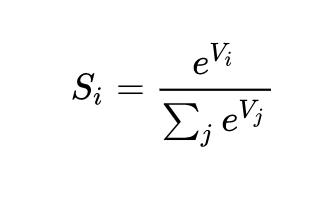
使用Softmax的信息來教學 —— 知識蒸餾
cosFormer:重新思考注意力機制中的Softmax
PyTorch教程4.4之從頭開始實現Softmax回歸





 PyTorch教程-4.1. Softmax 回歸
PyTorch教程-4.1. Softmax 回歸










評論