通過更深入地研究Sallen-Key濾波器的元件靈敏度,我們在數學分析中發現了一個“最佳點”,它允許設計簡單的單運算放大器濾波器,其性能可與更復雜的濾波器相媲美。這種方法在擴展Sallen-Key濾波器的實用性方面很有用。
多年來,已經設計了數十種濾波器拓撲結構,每種拓撲都有自己的優勢。然而,工程師通常依賴于這些拓撲中的一個小而流行的子組,這些子組可以使用“食譜”設計方法。他們為不太復雜的低階設計選擇更簡單的單運放濾波器。但是,當相關的食譜方法無法開發行為良好的復雜濾波器時,工程師通常會轉向更復雜的拓撲。但是,如果深入分析常見的單運算放大器拓撲(Sallen-Key濾波器),則可以得出一些有趣的結果。
典型的濾波器設計過程有三個主要階段。首先,根據系統要求確定要通過的頻率范圍、允許的通帶紋波等。接下來,您確定滿足要求的傳遞函數(數學濾波器描述),通常通過選擇標準類型之一:巴特沃斯、切比雪夫、貝塞爾、橢圓等。該過程中的這一步超出了本文的范圍,但可以從末尾列出的參考文獻中獲得詳細信息。
最后一步是設計和實現提供所需傳遞函數的電路。設計器通常遵循類似于以下內容的策略,該策略在應用于說明書拓撲時非常簡單:
將傳遞函數分解為二階部分。
選擇允許獨立合成每個二階函數的電路拓撲。
將每個級設計為獨立的二階濾波器。
串聯連接的二階濾波器。
此時可能會出現說明書方法的共同限制。單運算放大器濾波器通常對其無源元件值的變化表現出很高的敏感性,而具有高Q值的濾波器(即大多數高階濾波器)特別敏感。對于完美的無源元件來說,這種靈敏度不是問題,但實際元件僅在有限數量的標準值中可用。說明書計算可能需要 10.095k 電阻,但實際可用的最接近值可能是 10.0k。
實際組件值也因單元而異,并響應溫度和其他環境因素的變化。濾波器對這些分量變化的敏感性可能導致其明顯偏離其所需的頻率響應。在許多情況下,設計人員會轉向更復雜的濾波器拓撲。
薩倫基拓撲
Sallen-Key濾波器(基準電壓源1)是最常見的單運算放大器濾波器之一。其低通版本(圖1)具有以下設計公式:
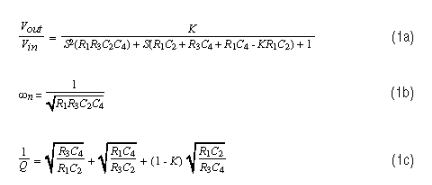
Q是“品質因數”(在固有頻率附近發生的峰值的量度),K = 1 + RB/R一個是直流增益。
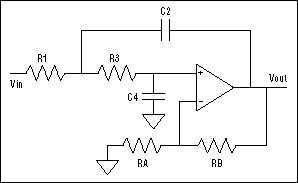
圖1.
過濾器對組件變化的敏感性
固有頻率和Q靈敏度有助于評估傳遞函數穩定性。對于Sallen-Key濾波器(在第2頁的參考文獻159中給出),這些靈敏度如下:
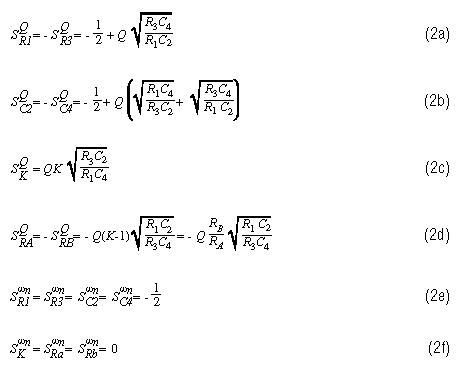
靈敏度用“S”表示。它的上標是正在評估其靈敏度的電路特性,其下標是正在評估其對該特性的影響的電路元件。因此,第一個靈敏度方程(2a)顯示了Q對R變化的靈敏度1或 R3.
S是提高元件變化以計算電路特性中相應變化的功率。例如,您可能已經注意到,所有固有頻率靈敏度的功率為 -1/2 或 0。當 S = -1/2 且分量變化系數為“A”時,固有頻率變化 A-0.5(即1/√A)。因此,新的固有頻率將是原始頻率除以√A。當 S = 0 時,頻率不會改變,因為 A0= 1。
參考文獻2更詳細地介紹了靈敏度,它包括上面列出的許多靈敏度方程的推導。參考文獻3和4也對這一重要主題進行了很好的處理。這些方程非常復雜,通常很難為所需的固有頻率和Q選擇六個無源分量,同時實現低Q靈敏度,除非您玩弄方程并注意到當增益(K)設置為1時發生的一些有趣的事情。
K = 1 簡化了薩倫鍵濾波器
我們可以通過選擇K = 1作為直流增益值來大大簡化Sallen-Key濾波器方程。在這種情況下,Q的方程(公式1c)簡化為

我們還發現,當K = 1時,Q對RA和RB的靈敏度為零(等式2d)。這并不奇怪。設置K = 1時,運算放大器的輸出直接連接到反相輸入,從而將運算放大器配置為電壓跟隨器,從而消除了RA和RB。
將Q的簡化方程(公式3)代入靈敏度方程2a和2c可簡化這些方程:

通過將電阻值設置為相等,可以進一步簡化Q對電阻的靈敏度。當R1和R3完全相等時,靈敏度為零。但實際電阻的值永遠不會真正相等。當它們偏離其標稱值時,靈敏度變為非零,但仍然非常小。例如,容差為 5% 的電阻會導致最壞情況的靈敏度

因此,5%的電阻變化會產生0.12%的Q變化,與其他靈敏度相比可以忽略不計。即使電阻值不相等,該靈敏度也在-1/2和+1/2之間。仔細觀察Q方程,可以發現設置R1 = R3的其他原因:
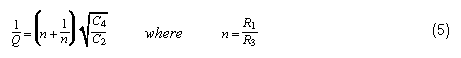
當 n = 1 時(即當 R3= R1),數量 (n+1/n) 的最小值為 2。因此,當Q = 1/2且電阻彼此相等時,濾波電容的值將相等。對于所有高于 1/2 的 Q(迄今為止最常見的情況),C2必須大于 C4.如果電阻不相等,則C的比值2到 C4必須做得更大。因此,為了最小化電容值的分布,電阻值應相等。
對于相等的電阻值,Q 的公式簡化為

重新排列這個方程,得到C2的C4,

我們可以將此表達式代入等式中:

n(公式 1b)并求解 C4:
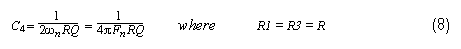
將此結果代入 C2 的方程(公式 7),我們得到

簡化的設計流程
將Sallen-Key濾波器增益設置為單位并設置R1 = R3,可通過求解兩個簡單方程來設計低靈敏度單運放濾波器。簡化的設計過程如下:
選擇合適的電阻值。
使用公式8和9求解電容值。
如果C2太大,則從較大的電阻值重新開始。
如果C4太小,則從較小的電阻值重新開始。
如果 C4 太小而 C2 太大,則您已達到 此篩選器的限制。
選取最接近計算值的標準值。
兩個例子說明了這種方法及其使用所帶來的好處。
將新方法與食譜方法進行比較
第一個例子來自作者幾年前所做的工作。為了盡量減少生產中的電路變化,他重新設計了一個電路(最初是用食譜技術創建的),以實現頻率為-3dB的4.8kHz的三階巴特沃茲低通濾波器。重新設計消除了修剪鍋及其相關的調整需求。
該濾波器需要一個Q = 1、固有頻率為4.8kHz的二階級。它最初采用Sallen-Key拓撲結構和參考文獻2第156至157頁的設計方法實現,該方法將電阻值設置為相等(R1 = R3 = R),電容值相等(C2 = C4 = C)。選擇 C = 0.001μF 會導致增益 (K) = 2 和 R = 33.2K。該電路的Q靈敏度如下:
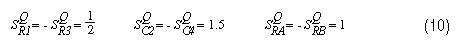
濾波器采用我們的新方法重新設計,使用相同的電阻值(33.2kΩ)。等式8和9得出C2 = 2000pF和C4 = 500pf。靈敏度如下:
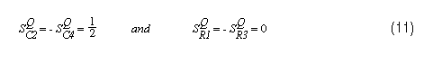
圖2顯示了用于仿真這些電路的原理圖,圖3顯示了SPICE仿真的結果。這些頻率響應圖是每個濾波器使用100%容差電阻和1%電容對每個濾波器進行5種不同“構建”的蒙特卡羅運行的結果。對于每個“構建”,SPICE 模擬器在其指定的公差范圍內隨機改變組件值。請注意,對于通帶中的所有頻率(尤其是接近固有頻率的頻率),新濾波器的變化明顯小于舊濾波器。
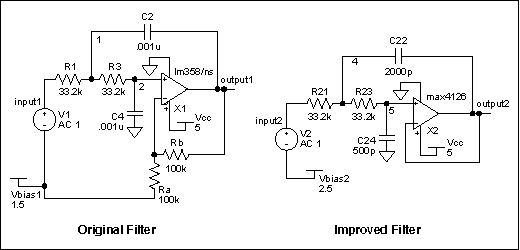
圖2.
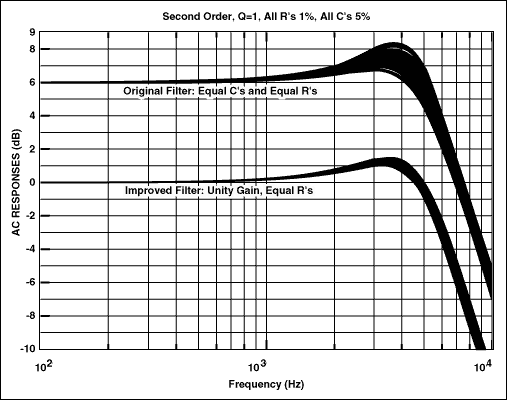
圖3.
同樣重要的是要注意,這些仿真結果并不是證明電路運行所需的唯一步驟;您還應該構建和測試電路。一旦SPICE仿真器指示交流性能與標稱元件值的實際電路相同,您就可以使用SPICE仿真器中常見的蒙特卡羅函數來評估電路響應如何隨元件的變化而變化。
級聯級實現高階濾波器
單位增益Sallen-Key方法有兩個缺點。它不能提供增益,對于高Q值濾波器,其電容比可能太大,無法實現濾波器。現有的放大器級通常可以提供所需的增益;但是,如果沒有,最壞的解決方案是增加一個單運放增益級。
高階濾波器通常需要至少一個具有非常高Q值的級。該級可以使用更復雜的拓撲來實現,而其他級則使用低靈敏度Sallen-Key電路實現。即使有Q值限制,Sallen-Key拓撲也可以執行傳統上使用多運算放大器拓撲實現的高階濾波器。以下示例顯示了設計此類篩選器的新過程,演示了與舊方法相比性能的顯著提高。標稱規格如下:
七階切比雪夫
0.05dB紋波
8kHz -3dB 頻率
增益 = 10
從這些客觀規范中實際推導傳遞函數超出了本文的范圍,但參考文獻詳細介紹了該主題。傳遞函數有三個復極對和一個簡單極點:
| Fn | Q |
| 7.834千赫 | 5.5662 |
| 6.560千赫 | 1.6636 |
| 4.492千赫 | 0.7882 |
| 3.162千赫 | 簡單 |
該濾波器的兩個版本的原理圖如圖4所示。一個是用食譜方法設計的,另一個是用我們的新方法設計的。每個電路最后級的單個運算放大器提供所需的增益和第七極。
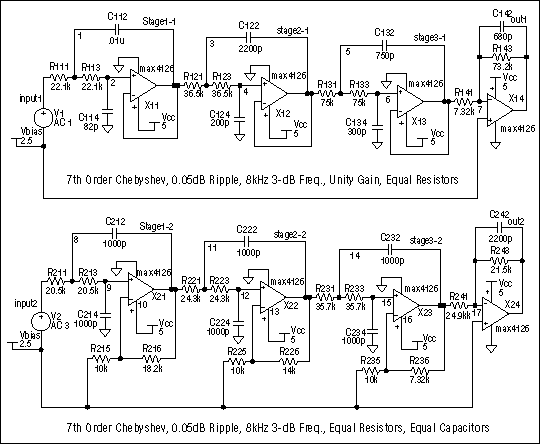
圖4.
圖5顯示了使用1%電阻和5%電容的蒙特卡羅分析結果。為了視覺清晰,結果在圖表上偏移。食譜版本在固有頻率附近具有大約28dB的變化,使該設計毫無用處。相比之下,單位增益/均阻版本在諧振附近的增益變化僅為4dB。
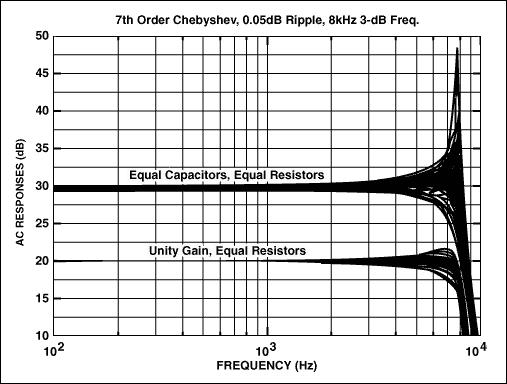
圖5.
薩倫基與雙二階濾波器
將這種七階Sallen-Key電路與相同傳遞函數的多運算放大器實現進行比較是很有趣的。雙二階濾波器是一種非常常見的三運放濾波器,具有低靈敏度和簡單的設計公式。其原理圖如圖6所示。使用參考文獻2中描述的技術,靈敏度如下:
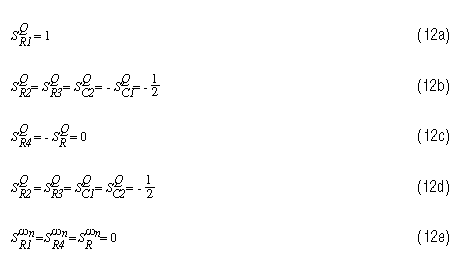
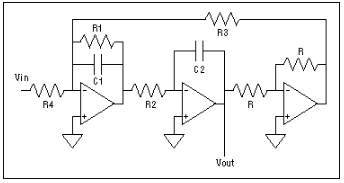
圖6.
我們規范的雙二階實現原理圖如圖7所示。同樣,末端的單運放級執行增益和第七個極點。圖8比較了單位增益Sallen-Key和雙二階實現的蒙特卡羅分析的頻率響應(為了清楚起見,結果再次偏移)。對于等效的組件,這兩個濾波器之間的性能沒有顯著差異。事實上,Sallen-Key的低頻增益變化略小于雙二階。
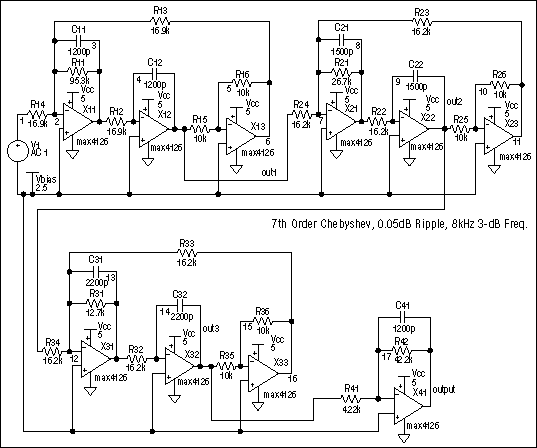
圖7.
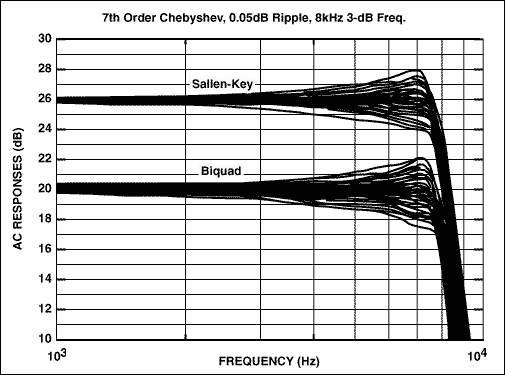
圖8.
下表列出了剛才討論的七階濾波器的三種實現方案的元件數、通帶變化和電容值的擴散:
| 電路 | 通帶變化 | 運算放大器 | 電阻 | 電容器 | 電容擴散 |
| 統一增益 S-K | 4分貝 | 4 | 8 | 7 | 從窄到寬 |
| 相等的遙控 S-K | 28分貝 | 4 | 14 | 7 | 窄 |
| 雙四體 | 4分貝 | 10 | 20 | 7 | 窄 |
將這些技術擴展到高通濾波器
我們還可以使用這些技術設計低靈敏度高通濾波器。等效的Sallen-Key高通濾波器如圖9所示。
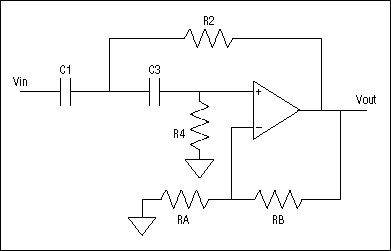
圖9.
其設計公式和靈敏度如下:

至于低通情況,我們可以通過設置 K = 1 和(在本例中)將電容器值設置為相等來簡化。然后,方程簡化為:

結果是電阻的兩個簡單公式,其中C1 = C2 = C:

因此,高通設計過程與低通情況非常相似:
為 C 選擇適當的值。
使用公式15a和15b計算電阻值。
如果 R4 太大,請使用較大的 C 值重新開始。
如果 R2 太小,請使用較小的 C 值重新開始。
如果 R2 太小而 R4 太大,則您已達到 此類型篩選器的限制。
選取最接近計算值的標準值。
為了說明這一過程,我們可以設計一個Q為1.0、固有頻率為8.0kHz的二階高通濾波器級。首先,選擇 C = 1200 pF。接下來,使用公式15a和15b設置電阻值:R2= 8.25kΩ 和 R4= 33.2kΩ。頻率響應與前面討論的低通濾波器的頻率響應一起繪制(圖 10)。
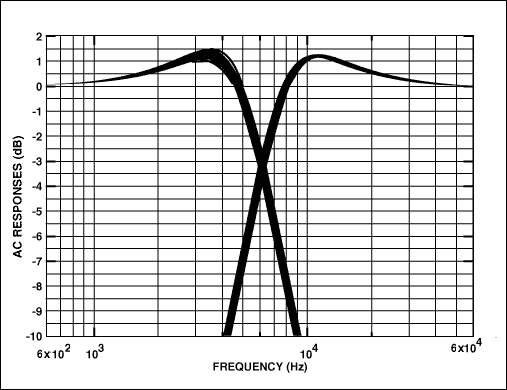
圖10.
高通濾波器的頻率響應擴散比低通濾波器更窄,特別是在峰值附近。這是因為我們最大限度地降低了對變化最大的元件(電容器)的敏感性。對于低通情況,對電阻的Q靈敏度最小,對電容的靈敏度為1/2。對于高通情況,對電阻的靈敏度為1/2,對電容的靈敏度降至最低。我們使用1%電阻和5%電容,因為低容差電阻比低容差電容更容易獲得。如果選擇5%電阻,則兩個電路的分布相似。
結論
通過更深入地研究Sallen-Key濾波器的元件靈敏度,我們在數學描述中發現了一個“最佳點”,允許設計簡單的單運算放大器濾波器,其性能可與更復雜的濾波器相媲美。這種方法有助于將Sallen-Key濾波器的效用擴展到高階高Q值濾波器的效用,并且對其他拓撲的類似研究可能會產生類似的結果。
審核編輯:郭婷
-
電容器
+關注
關注
64文章
6217瀏覽量
99541 -
濾波器
+關注
關注
161文章
7796瀏覽量
177997 -
運算放大器
+關注
關注
215文章
4930瀏覽量
172850
發布評論請先 登錄
相關推薦




 最大限度降低單運算放大器濾波器的元件變化靈敏度
最大限度降低單運算放大器濾波器的元件變化靈敏度











評論