數據轉換器的數據手冊經常提到，盡量減少數據轉換器時鐘的串擾非常重要。當被問及當它存在時會發生什么時，許多工程師都有“它會產生噪音”的見解。雖然這通常是一個真實的陳述，但在更深層次上理解這一點是有價值的，這樣設計工程師就可以更有效地理解和排除具有此類問題的電路。

閱讀本文后，讀者將了解數字數據信號到時鐘的串擾如何引起諧波失真和其他信號相關誤差問題。如果不了解機制，這些可能需要很長時間來診斷和修復。

在閱讀本文之前，了解本系列第一篇文章中的概念將有助于理解。

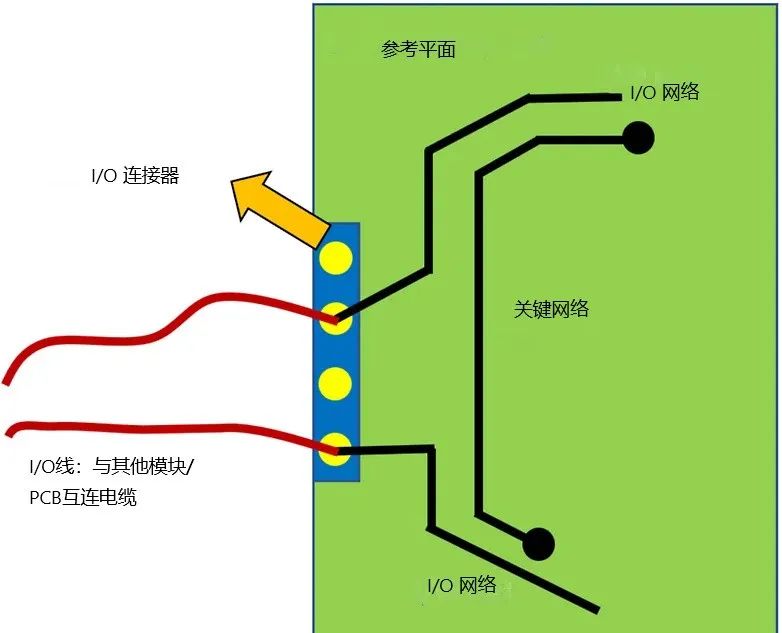
噪聲如何耦合到時鐘信號上

在討論數字位串擾對數據轉換器系統的影響之前，了解時鐘噪聲對數據轉換器系統的一般影響非常重要。

數據轉換器時鐘信號看起來像數字信號。怎么會容易串擾呢？

時鐘信號標記一個時間點 - 它越過數字信號閾值的點。如果上升/下降/轉換時間為零，則無論環境中存在噪聲，采樣時刻都將被精確定義。但現實世界的時鐘在上升和下降中是有偏差的。在此過渡期間，時鐘信號是模擬的。如果在閾值交叉附近的壓擺期間存在任何電壓串擾，則可以改變超過閾值的時間點。這會在時鐘上產生噪聲，通常稱為抖動。

時鐘噪聲對采樣輸入信號的影響

數據轉換器時鐘上的噪聲會影響采集數據轉換器模擬信號（即ADC輸入）樣本的時間點。如果模擬信號隨時間變化，則將采樣與最初預期的電壓不同的電壓。

時間誤差（即抖動）是時鐘轉換壓擺率的函數，與頻率無關。這通常是一個驚喜。量化：采樣電壓中的誤差是輸入信號電壓相對于時間的斜率，乘以時間誤差。

dv = （dv/dt） × dt = 斜率 × dt

請注意，該關系與時鐘頻率無關。唯一重要的是時鐘抖動的皮秒和模擬信號的壓擺率。

上述等式有許多重要含義，將在下面討論。

查看這種噪聲的另一種方法是將采樣信號視為時間的函數。即，

X (t) = sin (f × t).

時間分量由常規抖動時間分量代替。

X jittered (t) = X (t + jitter)

對于一個簡單的情況，我們可以假設抖動是正弦波。

抖動 = c × sin （ fj × t ）

這將產生結果：

X jittered (t) = sin (f × [ t + c × sin (fj × t) ] )

請注意，這與相位調制（PM）信號的等式相同。具有相位調制的正弦波是正弦波在其相位/定時位置調制的正弦波。如果ADC使用純時鐘對在Fj調制的正弦波進行采樣，則會產生與ADC使用時鐘對純正弦波進行采樣相同的樣本集，其采樣位置以Fj速率抖動。

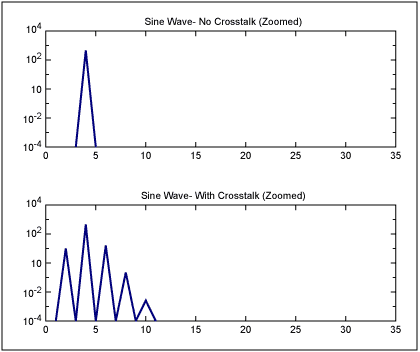
相位調制或正弦抖動正弦波的凈效應是，邊帶在調制頻率及其諧波的距離處出現在正弦波周圍。例如，圖1顯示了頻率為4的純正弦波和頻率為4的類似正弦波，頻率為2的PM調制/抖動。請注意，噪聲分量出現在頻率為2及其諧波的邊帶上。或者，給出精確的數字：“正弦波頻率”±N ד調制頻率”或 4 - 2 = 2、4 + 2 = 6、4 + 2 × 2 = 8、4 + 3 × 2 = 10 等。

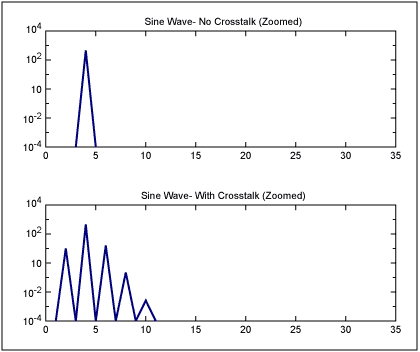
圖1.頻率為 4 的純正弦波，以及頻率為 2 的 PM 調制的相同正弦波（相當于頻率為 2 的時鐘串擾）。

現在，讓我們看一下上述一種更特殊的情況：當串擾/相位調制與原始信號處于同一頻率時。答案遵循與上述相同的原則和模式。邊帶出現在串擾頻率及其諧波的頻率距離處。圖2顯示了這樣一個例子：頻率為4的正弦波，頻率為4的PM調制/時鐘噪聲。請注意，邊帶出現在 4 + 4 = 8、4 + 2 × 4 = 12、4 + 3 × 4 = 16 等頻率下。

你能把這和諧波失真區分開來嗎？

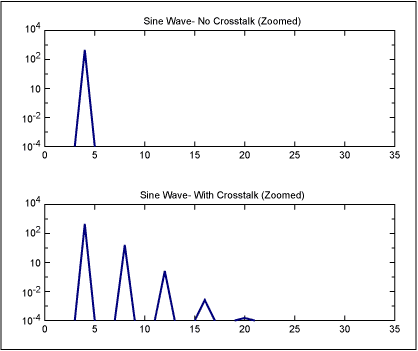
圖2.頻率為 4 的純正弦波，以及頻率為 4 的 PM 調制的相同正弦波（相當于頻率為 4 的時鐘串擾）。

結論

我們為什么要分析這個晦澀難懂的案例？因為這與ADC的數字數據信號串擾到時鐘時發生的情況直接相關。噪聲源是數字數據信號能量。由于電容耦合機制，這種能量在時鐘上產生與時鐘相同頻率的正弦“噪聲”。

審核編輯：郭婷