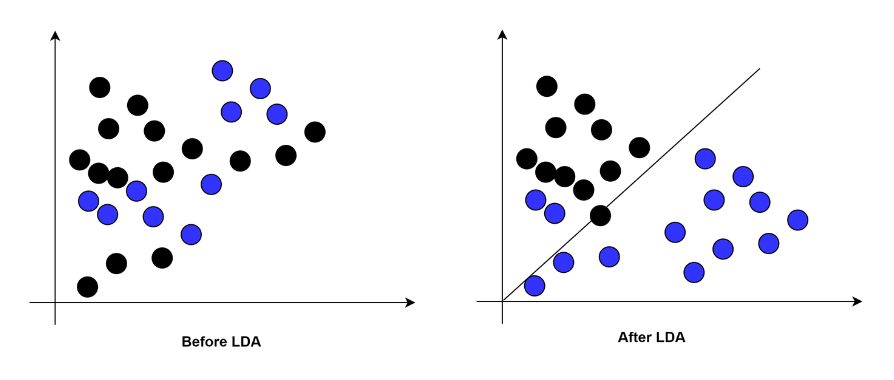
LDA(Linear Discriminant Analysis)是一種經典的線性分類方法,它的基本思想是將高維數據映射到低維空間中,同時最大化不同類別之間的距離和最小化同類別之間的距離,以此來達到降維和分類的目的。
具體來說,LDA 將數據分為不同的類別,并計算它們的均值和協方差矩陣。然后,它使用這些統計量來計算一個投影矩陣,將原始數據投影到一個新的低維空間中,使得不同類別的投影之間距離最大化,而同類別之間距離最小化。
在 MATLAB 中,可以使用 Classification Learner App 或 fitcdiscr 函數來進行 LDA 分析。以下是一個示例代碼,假設我們有一個包含 1000 個樣本和 10 個特征的數據集,并且有兩個類別:
%生成隨機數據 data=[randn(500,10)+1;randn(500,10)-1]; labels=[ones(500,1);ones(500,1)*2]; %計算LDA lda=fitcdiscr(data,labels); %可視化結果 gscatter(data(:,1),data(:,2),labels); holdon; line(lda.Mu(1,:),lda.Mu(2,:),'LineWidth',2,'Color','k'); line([lda.Coeffs(1,1).Constlda.Coeffs(1,2).Const]+... [lda.Coeffs(1,1).Linearlda.Coeffs(1,2).Linear]*[-44],... [lda.Coeffs(1,1).Constlda.Coeffs(1,2).Const]+... [lda.Coeffs(1,1).Linearlda.Coeffs(1,2).Linear]*[-44],... 'LineWidth',2,'Color','r'); line([lda.Coeffs(2,1).Constlda.Coeffs(2,2).Const]+... [lda.Coeffs(2,1).Linearlda.Coeffs(2,2).Linear]*[-44],... [lda.Coeffs(2,1).Constlda.Coeffs(2,2).Const]+... [lda.Coeffs(2,1).Linearlda.Coeffs(2,2).Linear]*[-44],... 'LineWidth',2,'Color','b'); axisequal; holdoff;
其中,fitcdiscr 函數可以計算 LDA,并返回一個 ClassificationDiscriminant 對象。這個對象包含投影矩陣、均值和協方差矩陣等信息。我們可以使用這些信息來進行分類或對新數據進行投影。
以上代碼中的 gscatter 函數用于可視化數據,而 line 函數則用于繪制分界線和均值點。
綜上所述,LDA 是一種非常有效的降維和分類方法,可以在不丟失太多信息的情況下將高維數據降到低維空間中,并且能夠在低維空間中進行有效的分類。在 MATLAB 中,可以使用 Classification Learner App 或 fitcdiscr 函數來進行 LDA 分析。
責任編輯:彭菁
-
函數
+關注
關注
3文章
4381瀏覽量
64994 -
線性
+關注
關注
0文章
204瀏覽量
25659 -
LDA
+關注
關注
0文章
29瀏覽量
10834
原文標題:LDA經典的線性分類方法
文章出處:【微信號:嵌入式職場,微信公眾號:嵌入式職場】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
LDA $88,SP完全不懂啊
基于LDA的SIFT算法在圖像配準中的應用
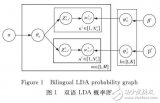
基于雙語LDA的跨語言文本相似度計算方法
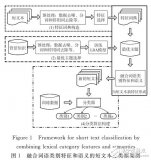
融合詞語類別特征和語義的短文本分類方法
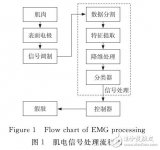
基于LDA分類器的模式識別方法
人臉識別經典算法三:Fisherface(LDA)
基于Hadoop平臺的LDA算法的并行化實現

基于隱含狄列克雷分配LDA分類特征擴展的廣告過濾方法
一種融合圖像紋理結構信息的LDA扣件檢測模型
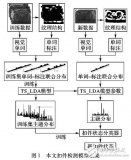
基于監督局部線性嵌入的中藥材分類鑒別研究
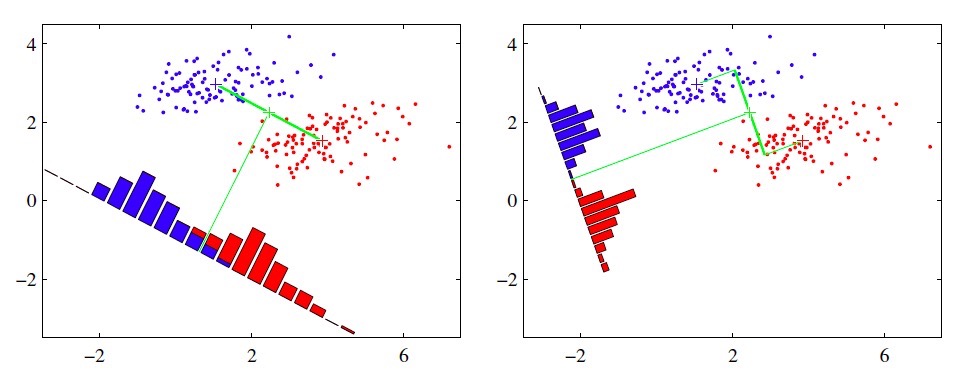
用PCA還是LDA?特征抽取經典算法大PK
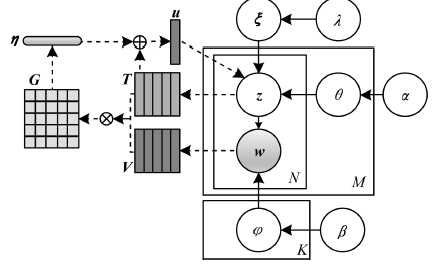
一種捕獲主題單詞信息的主題模型JEA-LDA



















評論