我們知道示波器的運作過程大致如下圖所示:
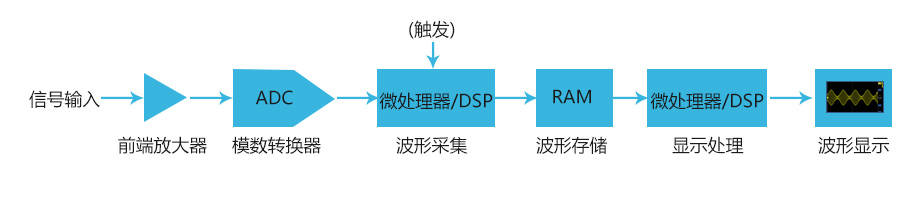
我們通過探頭給示波器輸入一個信號,被測信號經過示波器前端的放大、衰減等信號調理電路后,然后高速ADC模數轉換器進行信號采樣和數字量化,示波器的采樣率就是對輸入信號進行模數轉換時采樣時鐘的頻率,通俗的講就是采樣間隔,每個采樣間隔采集一個采樣點。比如1GSa/s的采樣率,代表示波器具備每秒鐘采集10億個采樣點的能力,此時其采樣間隔就是1納秒。
對于實時示波器來說,目前普遍采用的是實時采樣方式。所謂實時采樣,就是對被測的波形信號進行等間隔的一次連續的高速采樣,然后根據這些連續采樣的樣點重構或恢復波形。在實時采樣過程中,很關鍵的一點是要保證示波器的采樣率要比被測信號的變化快很多。
那么究竟要快多少呢?數字信號處理中的奈奎斯特(Nyquist)定律說, 如果被測信號帶寬是有限的,那么在對信號進行采樣和量化時,如果采樣率是被測信號帶寬的2倍以上,就可以完全重建或恢復出信號中承載的信息而不會產生混疊。
如下圖就是采樣率不足導致的信號混疊,可以看到采集到的信號和原始信號相比,頻率變小了很多。
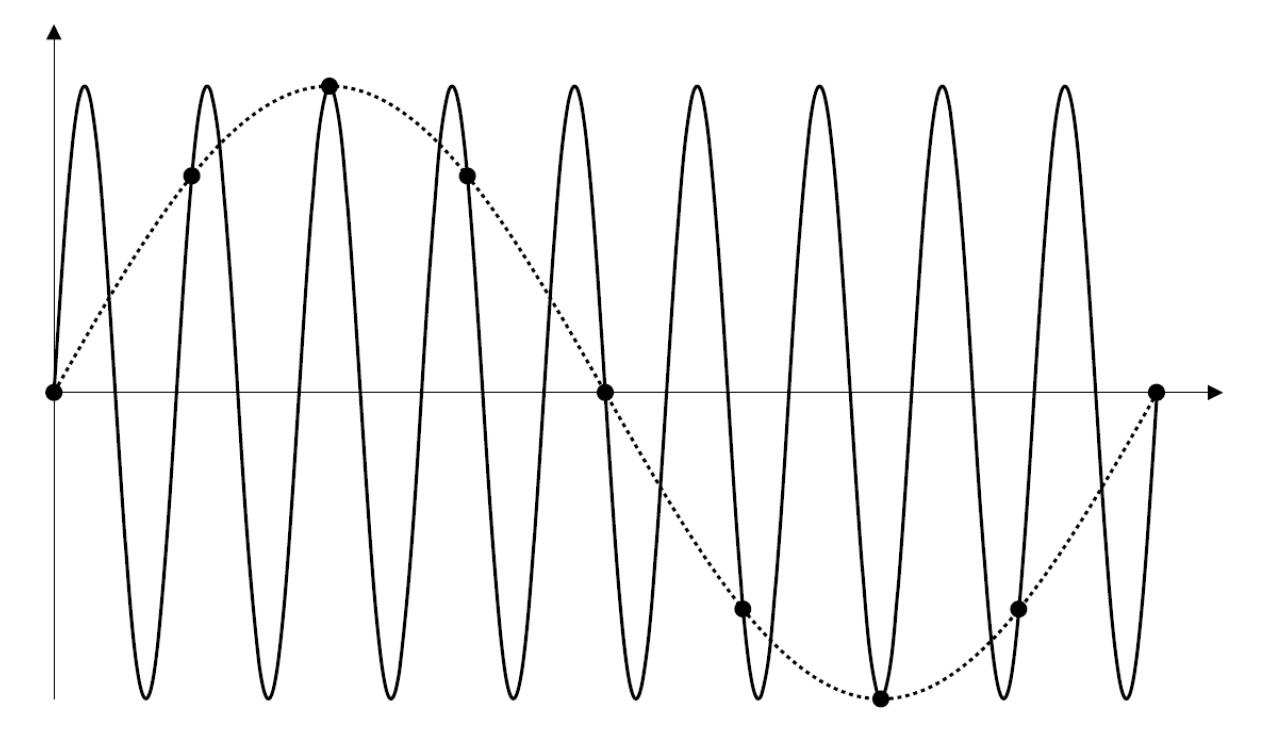
如果對示波器采樣率概念不是很了解的朋友,可以搜索查看我們之前的文章《示波器的采樣率概念詳解》進行學習。今天我們拋開理論,分別用示波器對1MHz正弦波,1MHz方波,100KHz鋸齒波,100KHz三角波進行實際測量一下,看看結果。
我們先用信號發生器生成一個幅值為10V,頻率為1MHz的正弦波輸入到示波器,通過調節存儲深度和時基,將采樣率降到我們期望的值。如下圖種可以看出示波器此時的時基是2ms,存儲深度是28K,采樣率 = 存儲深度 /(時基*14),采樣率正好就是1MSa/s。
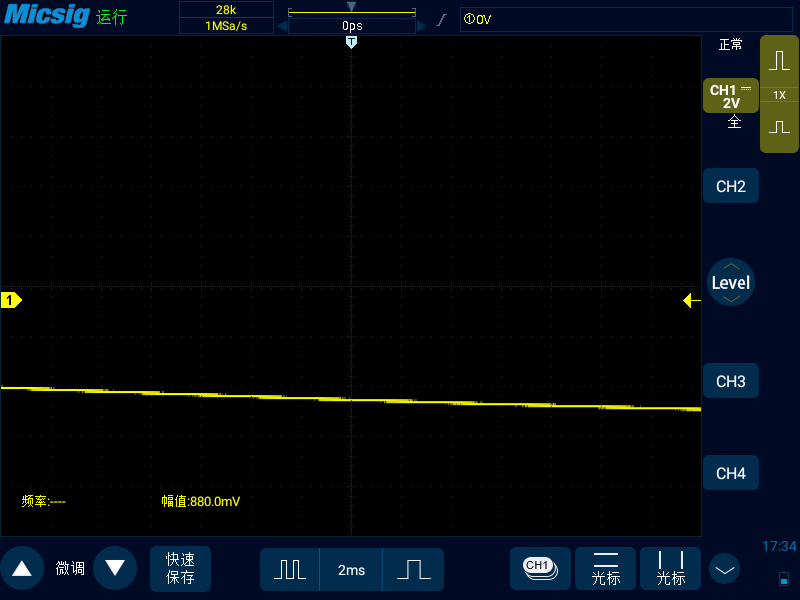
可以看到,當采樣率等于信號頻率的時候,示波器無法顯示正常的正弦波圖形,波形已經失真。我們將時基繼續打大,存儲深度固定不變,此時采樣率下降到了20KSa/s,可以看到示波器屏幕中可以看出信號是正弦波,但是信號的頻率從真實的1MHz下降到了1.668Hz,也就是發生了上述采樣率不足導致的信號混疊。
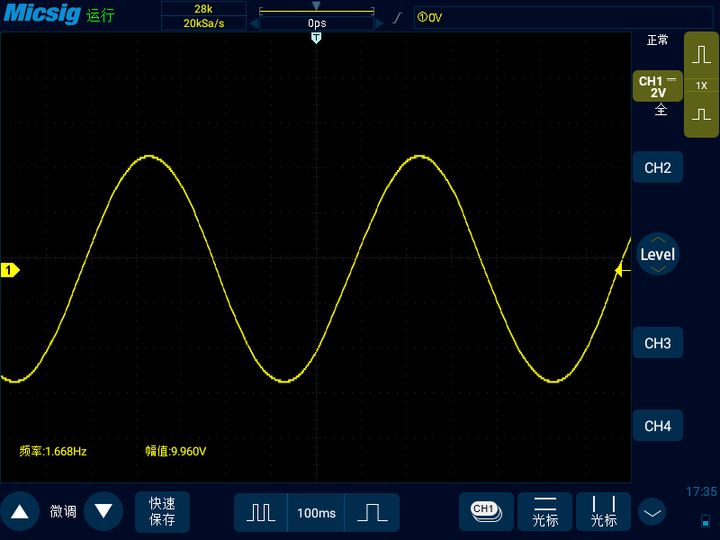
接下去我們將時基調小,這樣采樣率就變大了,一直調到采樣率為信號頻率的2倍和10倍來觀察信號變化,也就是2MSa/s和10MSa/s。下圖中左邊的信號就是2MSa/s采樣率下的,可以看到信號的頻率變回了1MHz,也就是信號正確的頻率值。但是原本的正弦波變成了三角波,波形已經失真。當采樣率變為10MSa/s時,也就是下圖右邊的信號,可以看到信號越來越接近正弦波的樣子了,但依然不是很漂亮。
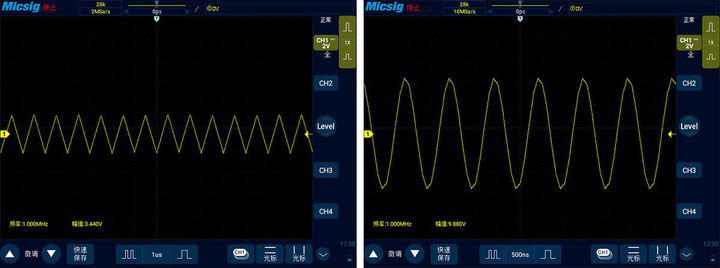
我們繼續減少時基,使得采樣率為信號頻率的20倍,也就是20MSa/s,此時可以看到就是比較漂亮的正弦波了,因此可以得出結論,觀察1MHz的正弦波,采樣率最好可以至少達到其20倍,才可以還原信號真實的樣子。
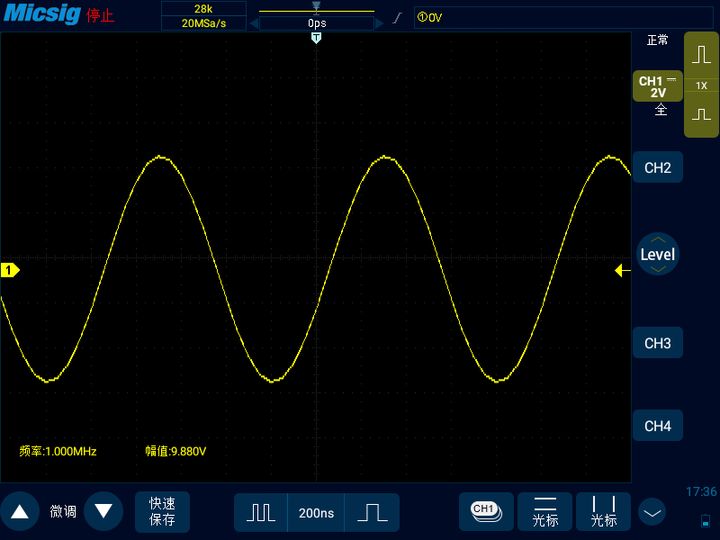
我們以同樣的方式對1MHz方波,100KHz三角波,100KHz鋸齒波進行實際測量,結果如下圖所示:
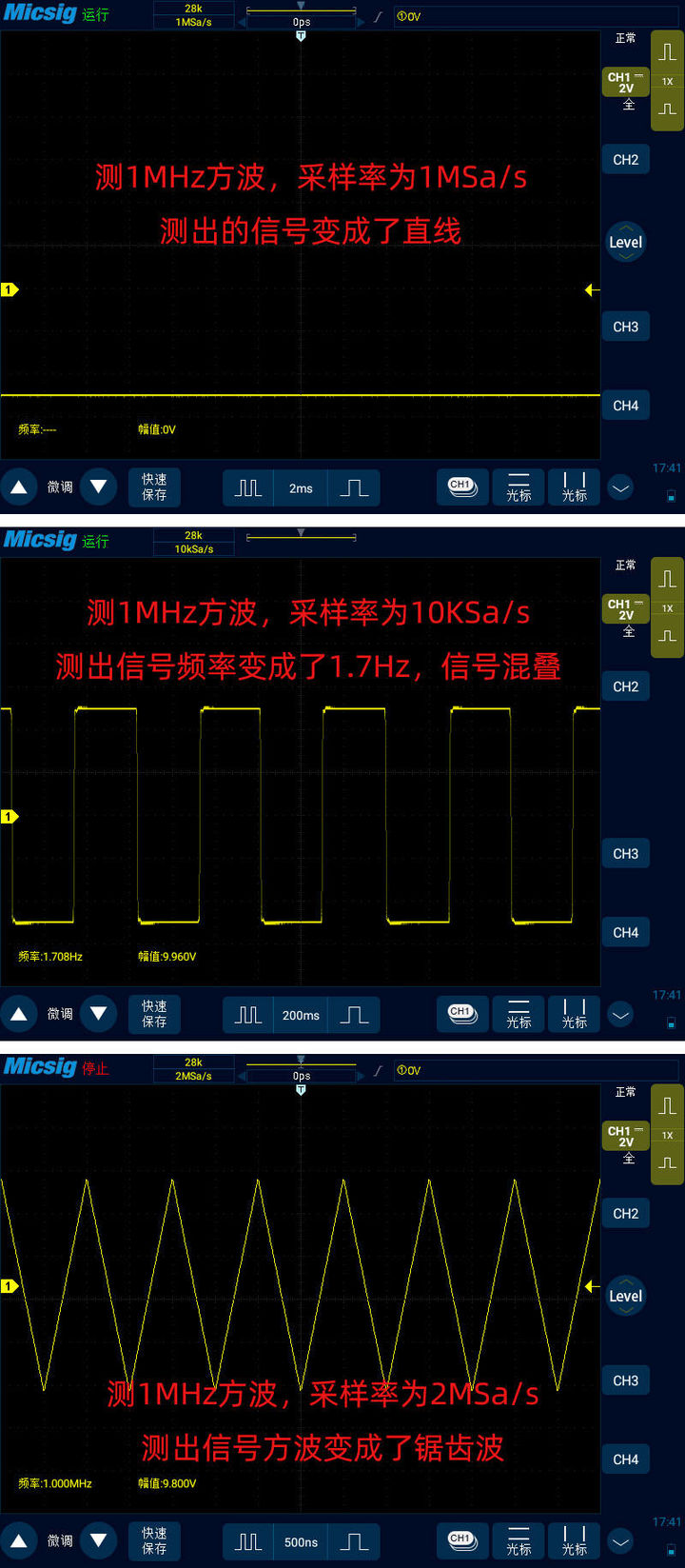
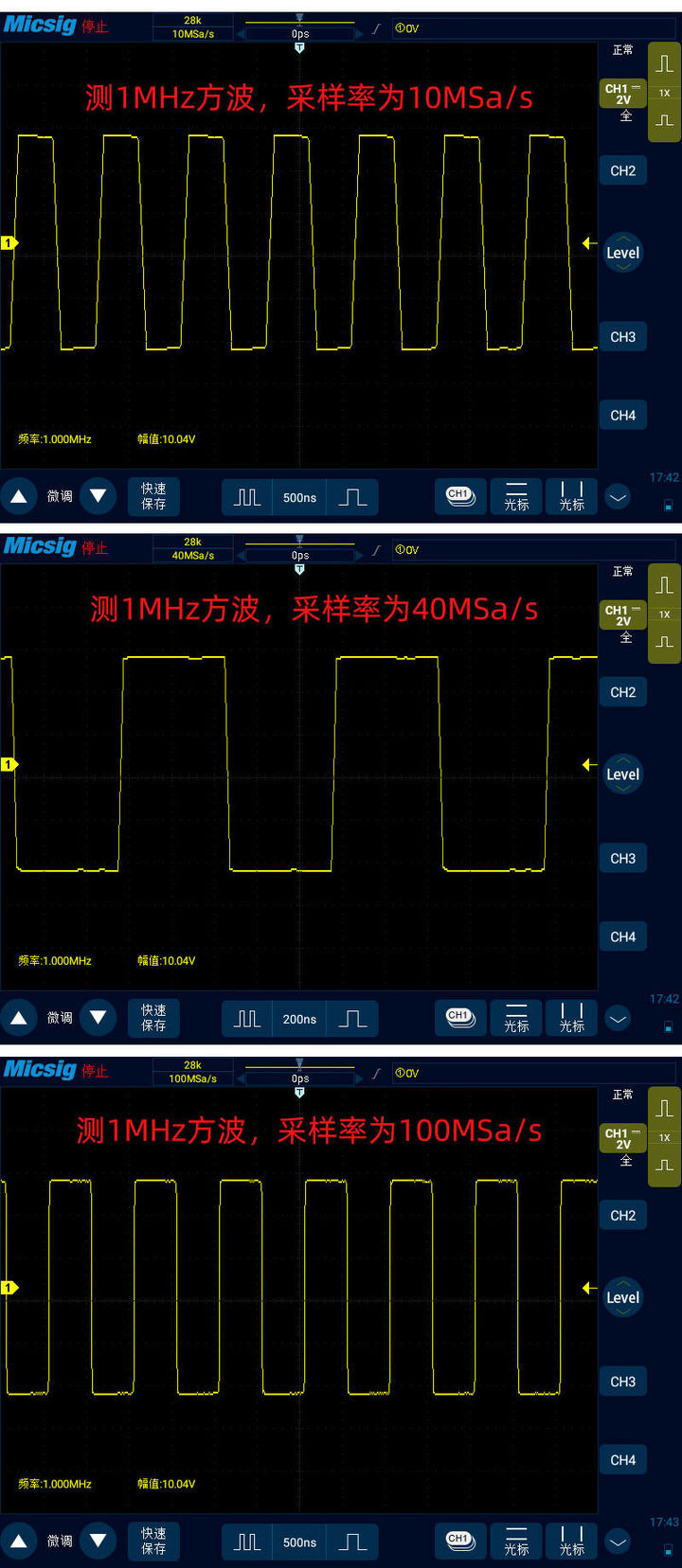
由此可以看出,測量1MHz方波對采樣率的要求比測量1MHz正弦波要高的多。測量1MHz正弦波在20倍的采樣率下就可以接近真實信號,而測量1MHz方波即使到了40倍上升沿依然坡度比較明顯的不直。
下面來看100KHz三角波:
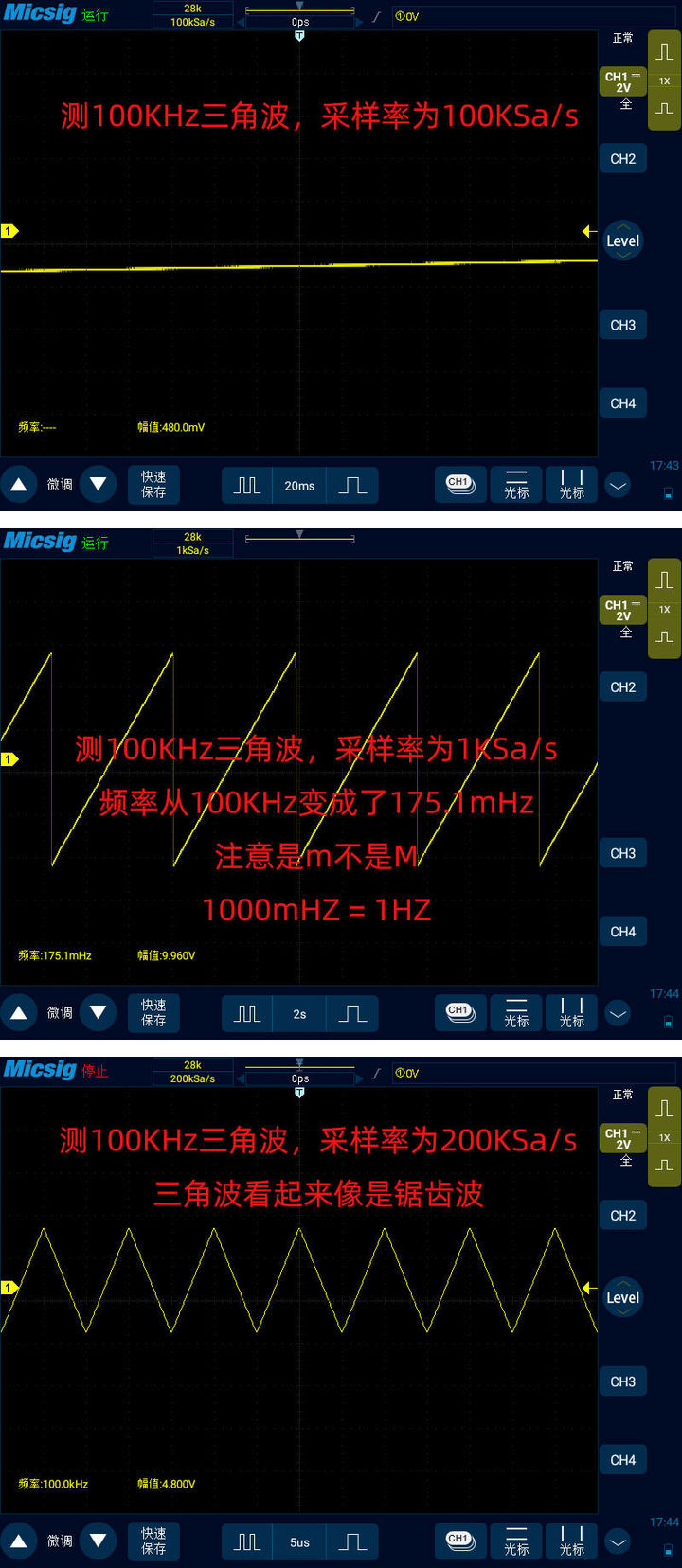
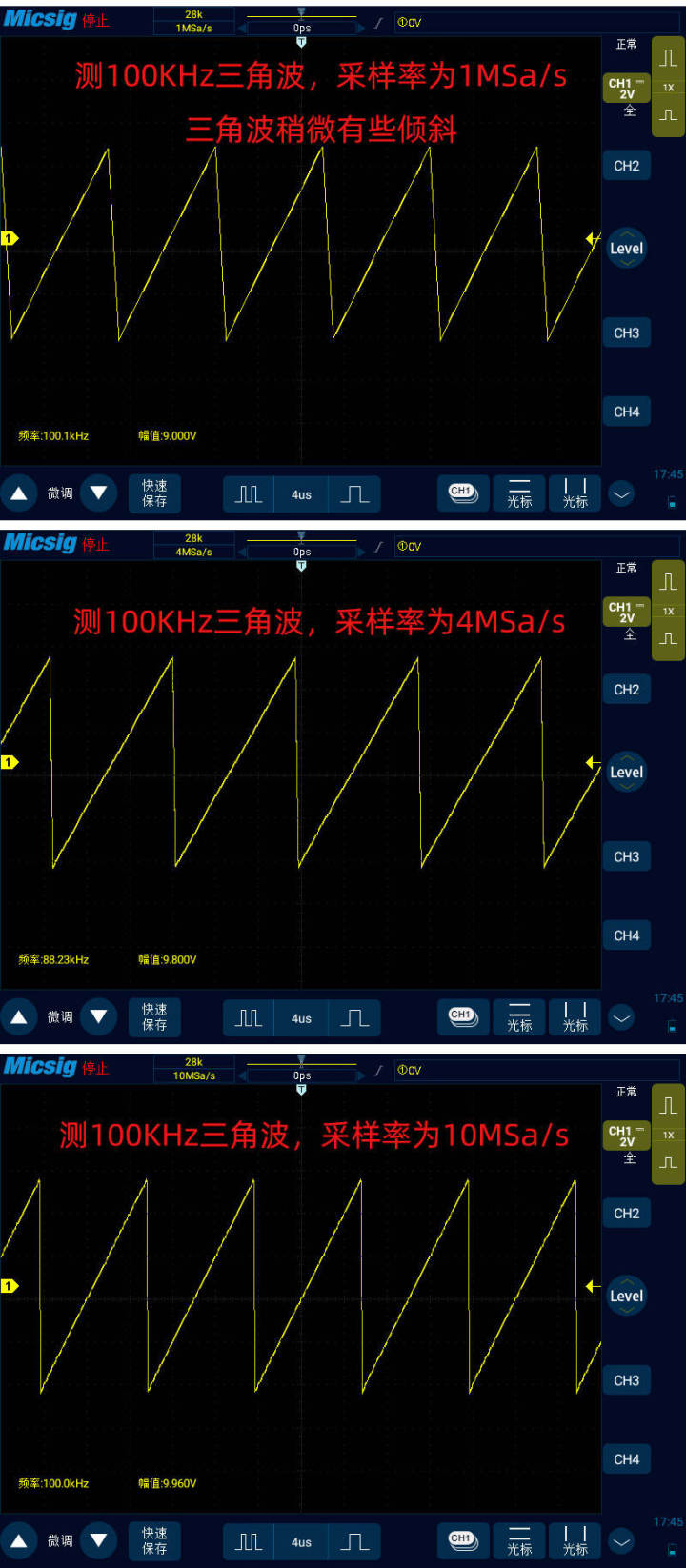
最后我們來看下100KHz鋸齒波:
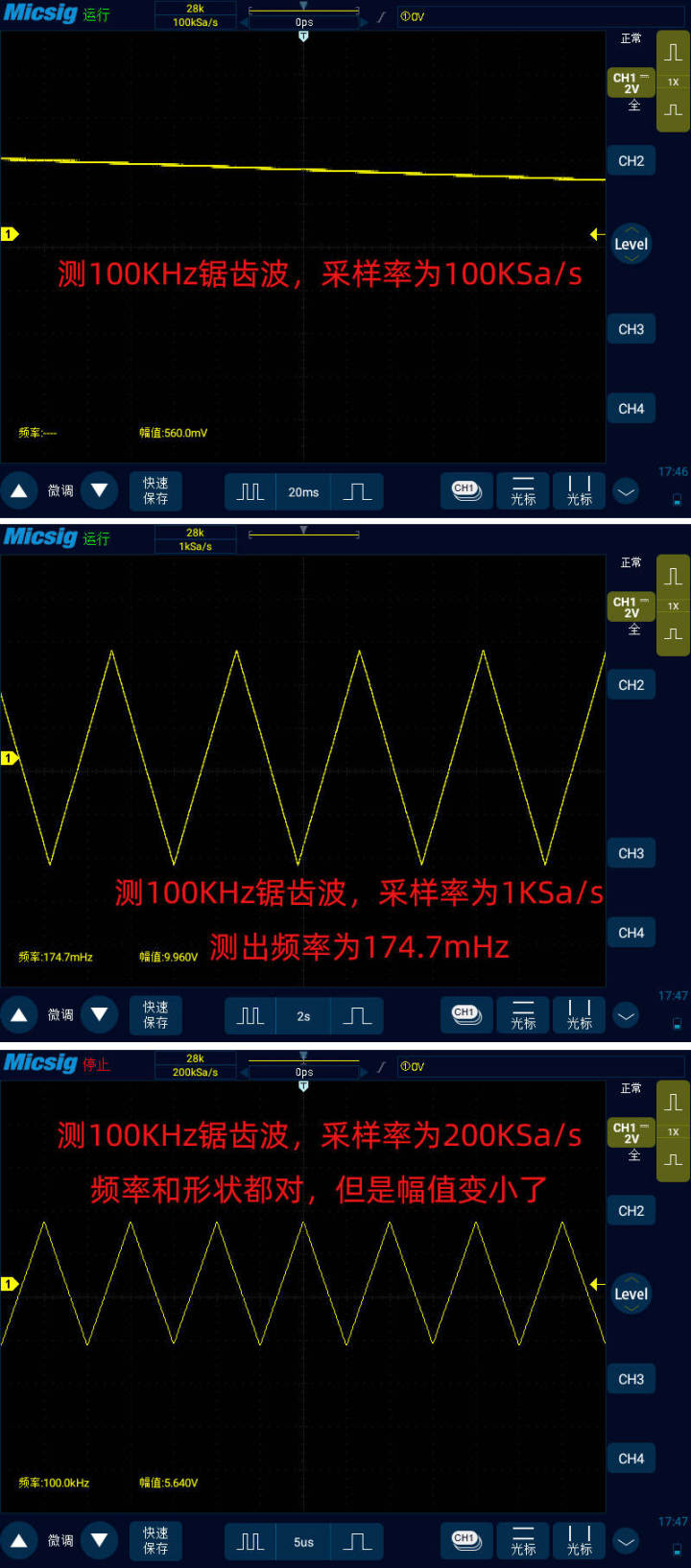
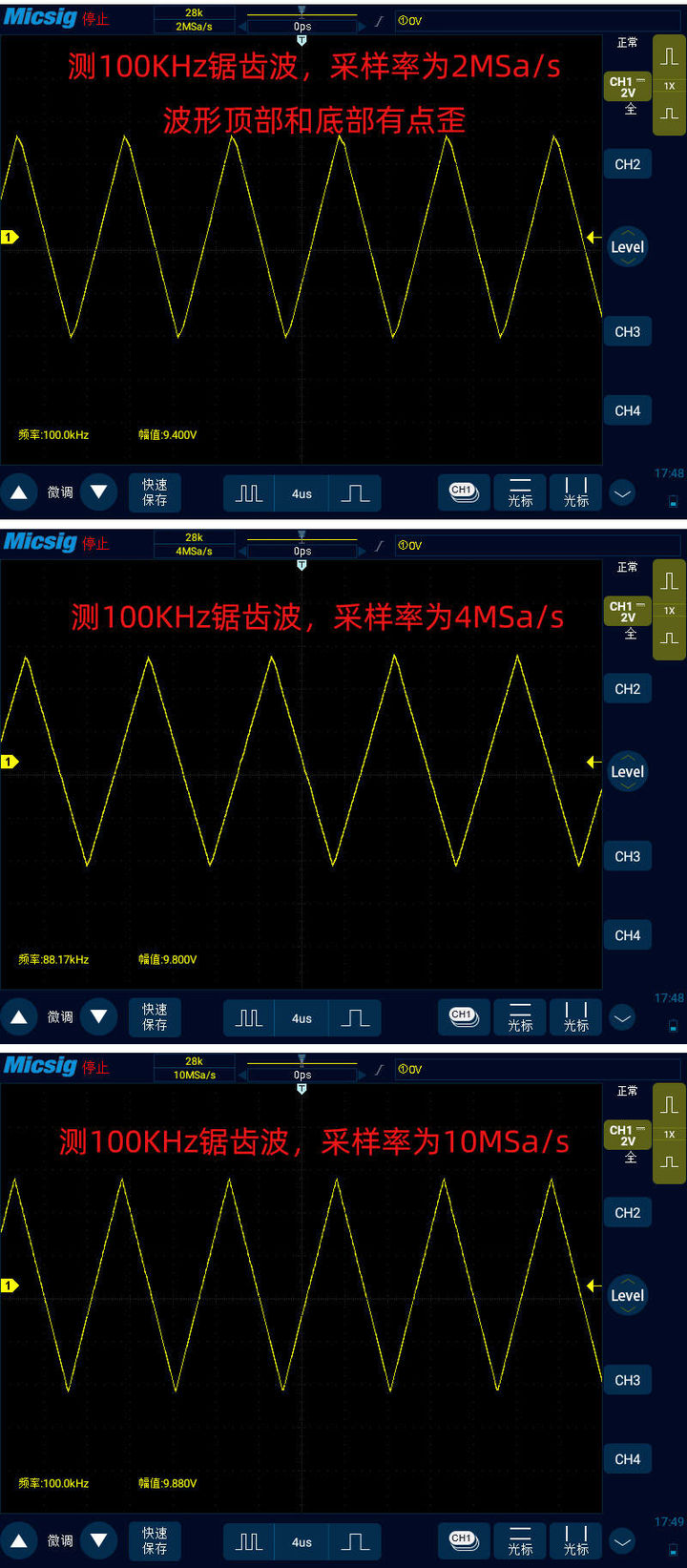
-
示波器
+關注
關注
113文章
6240瀏覽量
184801
發布評論請先 登錄
相關推薦
示波器多大采樣率足夠?實測示波器不同采樣率對不同波形的影響
請問PPS如何設置采樣率?
如何優化adc的采樣率
示波器和數據采集系統在位深與采樣率上的區別





 示波器測各種類型信號需要多大采樣率實測
示波器測各種類型信號需要多大采樣率實測












評論