2014年3月4日起，“11日超日債“成為了我國首例違約公募債，從此債券違約的案例陸續(xù)出現(xiàn)。因此建立債券違約預(yù)警模型對穩(wěn)定經(jīng)濟(jì)的健康發(fā)展起著重要的作用，而選擇有效的檢測指標(biāo)則可以提高模型的學(xué)習(xí)效率和準(zhǔn)確率，從而加快檢測速度。11日超日債（圖片來源于網(wǎng)絡(luò)）

近日，本源量子團(tuán)隊(duì)開發(fā)出量子mRMR算法（QmRMR），加速分析識(shí)別金融風(fēng)控領(lǐng)域企業(yè)債務(wù)違約行為。在篩選預(yù)警模型中有效指標(biāo)時(shí)，團(tuán)隊(duì)利用量子近似優(yōu)化算法（QAOA）對全局最優(yōu)指標(biāo)的選取進(jìn)行平方級加速，改進(jìn)了最大相關(guān)最小冗余（mRMR）算法，這一方法大大減少了債務(wù)監(jiān)測中的冗余分析指標(biāo)，將成功降低預(yù)測債券違約模型中的過擬合風(fēng)險(xiǎn)。

01mRMR算法減少債務(wù)信息“冗余”數(shù)據(jù)降維在金融數(shù)據(jù)分析中相當(dāng)重要，當(dāng)數(shù)據(jù)維度過高時(shí)，高維數(shù)據(jù)的各個(gè)維度間極易存在較強(qiáng)的相關(guān)性，容易產(chǎn)生大量冗余信息。這種情況下，我們無法直觀理解數(shù)據(jù)，在后續(xù)的數(shù)據(jù)挖掘、模型分析時(shí)也面臨困難。冗余的信息不僅使得模型難以收斂，內(nèi)存消耗大，甚至?xí)霈F(xiàn)過擬合的現(xiàn)象，直接干擾后續(xù)分析的結(jié)論。

降維的方法多種多樣，經(jīng)典的降維方法有主成分分析（PCA），奇異值分解（SVD)等方法。上面提到的兩種常見算法的優(yōu)點(diǎn)是通用性強(qiáng)，效果明顯，而缺點(diǎn)則是線性組合的現(xiàn)存數(shù)據(jù)與歷史數(shù)據(jù)無法并存，僅通過現(xiàn)存數(shù)據(jù)無法全面分析，且不具有可解釋性。特別是在金融領(lǐng)域中，各種指標(biāo)間的相關(guān)性較大，例如財(cái)務(wù)報(bào)表中形容償債能力的指標(biāo)就有流動(dòng)比，速動(dòng)比，長期負(fù)債比等。

而最大相關(guān)最小冗余（mRMR）算法和以上列舉的算法不同，它可以直接選取和剔除指標(biāo)。mRMR方法能夠在樣本指標(biāo)與目標(biāo)指標(biāo)（債券是否違約的標(biāo)簽）之間的交互信息達(dá)到最大的同時(shí)，使得選取指標(biāo)內(nèi)部的平均交互信息較少。而在選取指標(biāo)之前，是無法預(yù)先知道能夠選取的指標(biāo)個(gè)數(shù)，所以需要對mRMR模型進(jìn)行改進(jìn)，使得我們可以自由控制指標(biāo)選取個(gè)數(shù)的同時(shí)還能夠?qū)栴}轉(zhuǎn)化為二次二值無約束的優(yōu)化問題，也就是QUBO問題。并且我們在數(shù)學(xué)的原理證明了該改進(jìn)的正確性。

02利用量子近似優(yōu)化算法（QAOA）加速挖掘全局最優(yōu)指標(biāo)目前，原有的mRMR算法選取指標(biāo)所使用的增量搜索方法往往只能得到一個(gè)局部最優(yōu)結(jié)果。我們通過對算法的改進(jìn)可以在無約束的情況下自由選取指標(biāo)個(gè)數(shù)，在后續(xù)使用支持向量機(jī)進(jìn)行債券違約效果檢驗(yàn)時(shí)，發(fā)現(xiàn)改進(jìn)后的QmRMR算法選取的指標(biāo)能夠以高概率遍歷得出一樣的全局最優(yōu)指標(biāo)選取方案。在研究中，我們使用上市公司公開的財(cái)務(wù)報(bào)表作為分析指標(biāo)，來預(yù)測該公司發(fā)行的債券是否違約。我們基于償債能力、盈利能力、現(xiàn)金流量、資本結(jié)構(gòu)四個(gè)維度，利用改進(jìn)后的量子mRMR方法，在財(cái)務(wù)報(bào)表中選取出20個(gè)樣本指標(biāo)（將mRMR稍作改進(jìn)，就可以自由控制選取指標(biāo)的個(gè)數(shù)）。之后我們使用傳統(tǒng)的支持向量機(jī)來分類判斷后續(xù)的指標(biāo)選取是否有效，以及債券是否違約。在控制不同的指標(biāo)個(gè)數(shù)選取的情況下，分類的結(jié)果如下圖（其中各項(xiàng)指標(biāo)都是衡量分類器的標(biāo)準(zhǔn)，越接近1說明該分類器的性能越好）。

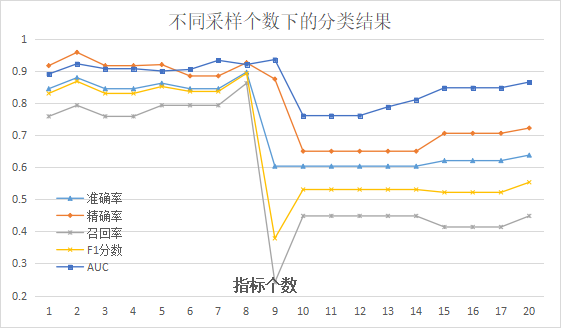
在不同樣本指標(biāo)個(gè)數(shù)下的分類結(jié)果：越接近1說明該分類器的性能越好上圖是在不同的指標(biāo)選取個(gè)數(shù)的情況下，五個(gè)衡量分類器的指標(biāo)的變換情況。綜合可以看出，我們在用量子mRMR選取8個(gè)最優(yōu)指標(biāo)時(shí)分類的效果達(dá)到最優(yōu)。以該8個(gè)指標(biāo)的選取過程為例，我們在實(shí)驗(yàn)中與使用經(jīng)典方法選取指標(biāo)得到的遍歷結(jié)果進(jìn)行對比，可以發(fā)現(xiàn)QAOA算法能夠以較高的概率得到和經(jīng)典一致的結(jié)果。下圖則展示了在迭代到80層的情況下，運(yùn)行量子線路得到最優(yōu)選取方法的概率。可以看出，隨著迭代的次數(shù)的增加，該概率總體呈現(xiàn)上升的趨勢，并且最終可以在每次運(yùn)行量子線路時(shí)都能夠以超過0.3的概率得到最優(yōu)解。

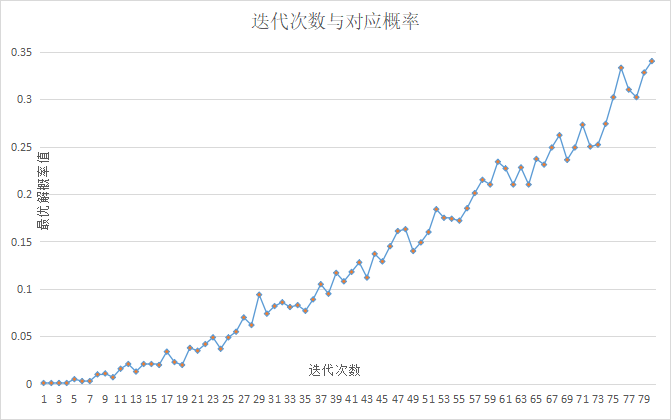
隨著算法迭代次數(shù)變多，單次運(yùn)行線路得到最優(yōu)選取方法的概率在選取8個(gè)指標(biāo)時(shí)達(dá)到較好的預(yù)測結(jié)果可以說明該8個(gè)指標(biāo)和目標(biāo)分類結(jié)果最大相關(guān)，且能夠從不同的維度來衡量是否會(huì)出現(xiàn)債券違約。我們在56次的實(shí)驗(yàn)對比中發(fā)現(xiàn)，QAOA算法均能夠以較高的概率得到和經(jīng)典遍歷一樣的結(jié)果，這證明了QAOA的穩(wěn)定性。相比于經(jīng)典計(jì)算，本源量子團(tuán)隊(duì)在此次研究中開發(fā)出的QmRMR算法能夠?yàn)槿謨?yōu)化指標(biāo)選取帶來二次加速，這對未來處理違約檢測等場景中的大規(guī)模金融數(shù)據(jù)有著重要的意義。