前向糾錯—FEC
前向糾錯(FEC)是增加數據通信的可信度的方法。
前向的意義是糾錯過程為單方向的,沒有錯誤的信息反饋。利用數據進行傳輸冗余信息的方法,當傳輸中出現錯誤,將允許接收器再建數據。
即一種差錯控制方式,信號在被送入傳輸信道之前會按一定的算法進行編碼處理,加入帶有信號本身特征的冗余碼,在接收端按照相應算法對接收到的信號進行解碼,從而找出在傳輸過程中產生的錯誤碼并將其糾正。比較經典的編碼解碼方式例如漢明碼、BCH碼、RS碼等。
漢明碼(Hamming Code),是在電信領域的一種線性調試碼,以發明者理查德·衛斯里·漢明的名字命名。漢明碼在傳輸的消息流中插入驗證碼,當計算機存儲或移動數據時,可能會產生數據位錯誤,以偵測并更正單一比特錯誤。
簡單來說,前向糾錯(FEC)就是在數據中添加冗余進行傳輸,檢驗出錯誤后通過冗余可以恢復原本的數據。漢明碼是一種可用于前向糾錯(FEC)的編碼和解碼方式。
一
奇偶校驗
漢明碼使用到了奇偶校驗的方法,所以先復習一下——奇偶校驗。
示例中高亮位為校驗位,如果傳輸過程中,某一數據位發生錯誤,則檢驗便會不符合校驗規則。
奇校驗:所有傳送的二進制代碼的數位(含字符的各數位和校驗位)中,“1”的個數為奇數。
例:1001 1011——0 1001 1011因傳輸的原始數據中,1的位數為5,奇數,所以校驗位寫0。
偶校驗:所有傳送的二進制代碼的數位(含字符的各數位和校驗位)中,“1”的個數為偶數。
例:1001 1011——1 1001 1011因傳輸的原始數據中,1的位數為5,奇數,所以校驗位寫1。
二
漢明碼
1
什么是冗余
冗余,在漢明碼中是附加在數據中的校驗位,它是附加在數據的比特位之間,是一種二進制位,可以通過冗余位來檢驗數據錯誤和恢復正確的數據。那么,一個數據中的冗余位,應該是多少個,可以使用(式 2-1)計算:
2n >= m+n+1 (式 2-1)
(n:冗余位位數。m:數據位數。)
例:傳輸一個8位的數據0x9B,二進制表示為1001 1011,則計算n的結果為4:24>=8+4+1。
2
怎么分組
如下圖2-1,假設有一個7位的數據,每個位編號1,2......7。分為3組:C1,C2和C3。
C1:1,2,4,5
C2:2,3,5,6
C3:4,5,6,7
始終假設,只有一個錯誤存在其中。
如果,只有C1區錯誤,C2和C3區沒有錯誤,根據這個條件,可以看出,C2中2,3,5,6是沒有錯誤的,C3中4,5,6,7沒有錯誤,說明出錯的是1。再來一次,如果C2和C3區有錯誤,C1區沒有錯誤,這次我們可以排除C1中1,2,4,5沒有錯誤,C2和C3只有一個錯誤,則出錯的肯定是6。
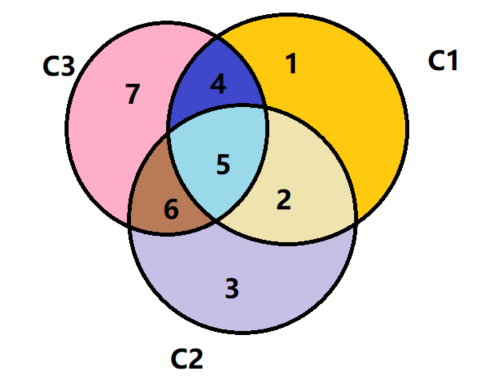
(圖 2-1)
3
編碼
接下來,我們開始編碼了,使用奇校驗方式,還是上面那個數字為例:0x9B,二進制表示位1001 1011,這是一個8位的數據,所以冗余位的個數位4,總的數據位數為12。
到這里,又出現了一個問題,冗余碼放哪些位置呢?前面or后面?都不是,冗余碼(奇偶校驗碼)穿插在數據中放置,放置的位置和冗余碼數量有關,即位置在:20,21,22,23,24……2n-1。
示例為4個冗余位,則放置在第1,2,4,8位的位置上,如下圖2-2,剩下的數據位,我們順序填入需要編碼的數據,如下圖2-3。

(圖 2-2)

(圖 2-3)
這時候,我們發現了,圖中我們不僅對數據位編號,并且表示為二進制,原因就是,數據位編號的二進制表示,是我們進行數據位分組的依據。接下來,我們開始分組:
①二進制編號第一位為1的:1,3,5,7,9,11 ————20
②二進制編號第二位為1的:2,3,6,7,10,11 ————21
③二進制編號第三位為1的:4,5,6,7,12 ————22
④二進制編號第四位為1的:8,9,10,11,12 ————23
高亮的編號位是每組對應填入奇偶檢驗位的位置,對實際的數據位數采用奇校驗:
①組:1的個數為4,因此20處填入1
②組:1的個數為2,因此21處填入1
③組:1的個數為3,因此22處填入0
④組:1的個數為2,因此23處填入1
綜上,編碼后的數據為1001 1101 0111,如圖2-4所示。

(圖 2-4)
4
檢錯與糾錯
數據傳輸過程中,如果沒有錯誤,校驗通過,則皆大歡喜。如果數據出錯了呢,我們便要進行檢錯(找到錯誤)和糾錯(糾正錯誤)。在此之前,我們還是要重復一下,漢明碼最多只能糾錯一個比特位的數據錯誤。我們接下來開始。
假設數據位編號為7的數據,在傳輸過程中,不小心,從”1“變成了”0”。如圖2-5。

(圖 2-5)
檢錯:
①奇校驗第一組:目前數據位11,9,7,5,3,1數據表示為010111,此時數據位中1的個數為4,不滿足奇校驗,說明這一組數據中某一個位出錯。因為要滿足奇校驗,所以需要補1滿足。

(圖 2-6)
②奇校驗第二組:目前數據位11,10,7,6,3,2數據表示為000011,但是此時數據位中1的個數為2,不滿足奇校驗,說明這一組數據中某一個位出錯。因為要滿足奇校驗,所以需要補1滿足。

(圖 2-7)
③奇校驗第三組:目前數據位12,7,6,5,4數據表示為10010,但是此時數據位中1的個數為2,不滿足奇校驗,說明這一組數據中某一個位出錯。因為要滿足奇校驗,所以需要補1滿足。

(圖 2-8)
④奇校驗第四組:目前數據位12,11,10,9,8數據表示為10011,此時數據位中1的個數為1,滿足奇校驗,說明這 一組數據正確。只需要補0。

(圖 2-9)
糾錯:
重新校驗之后,把補上的數位按照從高位到低位排列得出:0111,也就是7。所以,錯誤的數位編號為7,只需要將收到的數據的第七位取反,即得到正確的發送方發送的數據:1001 1101 0111。
-
通信
+關注
關注
18文章
6042瀏覽量
136138
發布評論請先 登錄
相關推薦
利用ADS1293與ARM進行SPI數據通信的程序設計該注意什么?
ADS9110使用絲線SPI進行ADS數據通信,但是在調試頁面讀取不到數據,示波器上也未顯示傳輸數據波形,怎么解決?
意法半導體推出新款增強版移動數據通信模塊
OSI七層模型與數據通信的關系
華為發布數據通信未來技術趨勢報告
瀾起科技發布數據保護和可信計算加速芯片
華為成功舉辦數據通信創新峰會北非站,助力非洲網絡智能化發展

數據通信網關是什么?數據通信網關的功能作用
速銳得深入解析吉利幾何CAN總線數據通信網絡的拓撲層級框架技術





 【技術】FEC—數據防丟失,提升數據通信可信度!
【技術】FEC—數據防丟失,提升數據通信可信度!












評論