摘要：由于成像光學系統固有的特性，以及鏡頭成像平面與物體平面存在的傾斜角和轉角，使得獲取的圖像存在著非線形幾何畸變。在對圖像進行定量分析和檢測之前，必須消除這些畸變。為此，本文提出了一種以校正徑向幾何畸變為主的非線性校正方法。討論了控制點的選取原則，建立了三次多項式的畸變校正模型；分析了不同灰度重建方法的特點，進行了仿真實驗，校正結果良好，在成像測量應用中有很好的實用價值。

在用光學鏡頭攝像機采集圖像時，由于物面與像面的不平行投影、鏡頭畸變和攝像機質量等因素的影響，其采集的圖像存在著幾何畸變。尤其是現在廣泛用于監視系統的短焦距，廣角鏡頭系統，畸變較為明顯，在進行基于圖像分析的運動檢測、模式匹配等定量分析時，就需要對這類系統的畸變進行校正，以產生精確的低失真的圖像。

鏡頭的幾何畸變有徑向和切向兩類，通常徑向畸變比切向畸變大的多，因此，在一般的工作中主要考慮徑向畸變，而忽略切向畸變。徑向畸變主要是由鏡頭的徑向曲率不同造成的，有枕形和桶形畸變兩種。研究表明，在一般情況下，對廣角鏡頭的成像，只要采用三次多項式變形技術和雙線性插值法，就可消除這類失真，得到理想的圖像。其中，采用多項式擬合進行空間坐標變換是關鍵性的一步。

1 幾何畸變校正的原理

在幾何畸變圖像校正中常用一幅基準圖像去校正畸變圖像，設基準圖像的坐標為(u，v)、畸變圖像坐標為(x，y)，重采樣成圖法采用的二維多項式數學模型為

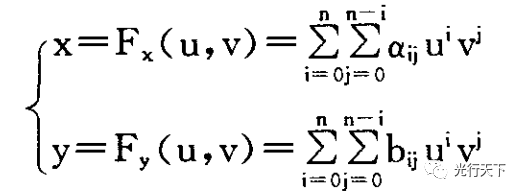
（1）

式中：n為多項式的項數，aij和bij為各項系數。

設基準圖像為g(u，v)，而畸變圖像為f(x，y)，對于圖像中的同一個點，假設其灰度值是不變的，即

g(u，v)=f(x，y) （2）

式(2)為圖像幾何畸變校正的基本公式。基準圖像中的X、Y為整數，而由式(1)計算得到的X、Y不一定為整數，必須進行灰度插值運算。

2 灰度插值方法比較

常用的插值方法有最鄰近點法、雙線性內插法及三次卷積法三種。

a. 最鄰近點法

最鄰近點法的實質是取原始畸變圖像4個鄰近點中距離坐標(x，y)最近的點(x'，y')的灰度作為該點的灰度，即g(u，v)一f(x'，y')

其 中 ：x'=IFIX(x+0.5)；y'=IFIX(y+0.5)。

最鄰近點法的優點是算法非常簡單并且保持原光譜信息不變；缺點是幾何精度較差，使校正后的圖像不具有連續性，表現為原來光滑的邊界出現鋸齒狀。

b. 雙線性內插法

雙線性插值法利用4個鄰近點的灰度在兩個方向上作線性插值。具體算法為

設點(u，v)落在(x，y)、(X+1，y)、(x，y+1)和(x+1，y+1)之間，則復原點(u，v)上的灰度值為：

g(u，v)=(1一α)(1一β)f(x，y)+α(1一β)f(x+1，y)+(1一α)βf(x，y+1)+αβf(x+1，y+1) (3)

式中α=u-x，β=v-y。

雙線性插值法具有計算簡單、幾何上準確度較高、能克服灰度不連續等優點，缺點是由于亮度內插，圖像的光譜信息發生了變化，易造成高頻成分的損失，使圖像變的模糊。

c. 三次卷積法

三次卷積法是利用一個一元三次多項式來近似理論上的最佳重采樣函數

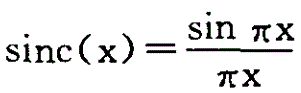
，相當于在(x，y)周圍的4*4鄰域內進行二維重采樣，由于參與運算的點數多造成計算量較大，優點是不僅圖像的亮度連續以及幾何上比較精確，而且還能較好地保留高頻成分。

綜合考慮計算速度和精度的要求，本文采用了雙線性內插法進行畸變校正。

3 控制點(GCP)的選取

多項式(1)中的各待定系數可以利用K個控制點坐標按最小二乘法原理來求得，即使最小二乘誤差

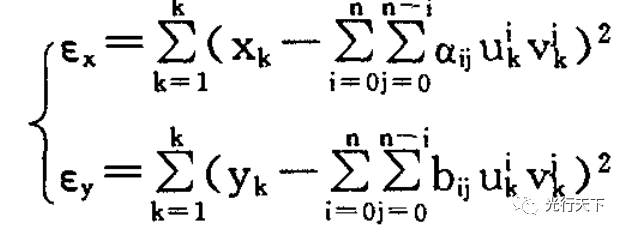
（4）

為最小。由于多項式項數N與其階數n有著固定的關系，即N=(n+1)(n+2)/2

因此，根據控制點數據用最小二乘法來計算未知系數時，控制點的數目必須不小于N個。在本文中采用了三次多項式，至少需要選擇1O個控制點。另外在選擇控制點時要注意控制點的分布，為了輸出圖像的精確，應使控制點分布均勻，在靠近圖像的邊界和四角頂點的地方要保證有控制點，以保證輸入畸變圖像和輸出校正圖像大小相等。

4 圖像畸變校正過程

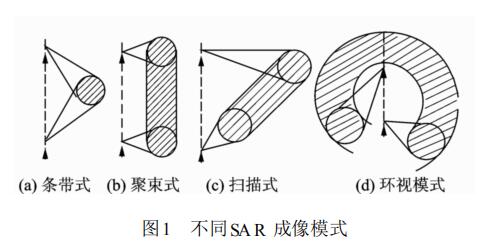
在實際的光電測量系統中獲得了如圖l所示的畸變圖像，物方原來的直線成像后變成了曲線，顯然要得到實際物體正確的線度信息，必須對此非線性畸變進行修正。畸變校正可以按以下三個步驟進行：

(1)建立原始畸變圖像與校正后圖像的坐標系。確立校正圖像的原點，圖像大小(行數和列數)等。

(2)根據上述中控制點的選取原則在原始畸變圖像與標準空間中確定控制點。

(3)選擇畸變數學模型，由于原始圖像是復雜的非線性畸變(見圖1)，為得到較好的輸出圖像至少要選擇三次多項式校正(tk數越高圖像的擬合越精確，但是也會帶來計算量的巨增)，然后利用上一步驟中獲得的控制點數據，確定多項式的未知參數，并分別根據最鄰近點法和雙線性內插法對畸變圖像進行灰度重建。

5 仿真實驗及分析

實驗條件：

(1)攝像頭，PH380型，鏡頭焦距f=3.5mm的CCD攝像頭。

(2)成像數據采集器320*240(pixe1)。

(3)樣本圖樣為8*8的正方形網格測試圖。

采用三次多項式畸變校正技術以后得到的實驗結果：

圖2所示為采用最鄰近插值法復原的圖像。

圖3所示為采用雙線性內插法得到的圖像。

從實驗結果看，無論采用最鄰近插值還是雙線性內插方法都對因鏡頭不完善所致的畸變得到明顯的校正，并且也驗證前面所述的采用雙線性內插法復原的圖像相比最鄰近法采樣精度和幾何上更為精確，圖像亮度連續，避免了出現圖2中的鋸齒狀線條邊緣。

本文的方法是一種比較便捷的幾何畸變校正方法，只要樣本圖做的好，并使樣本圖盡量垂直于光軸，則會使本方法更有效。從實驗結果中，我們也注意到，校正后像的邊緣有極小部分像點無圖像信息，這是因采用反向映射法計算時，在邊緣處的坐標超出了實際畸變圖像的坐標范圍，無可用象素點所致，但在實際畸變圖像的每點都已獲校正，故不影響像的校正結果。