遙想當年，與傅里葉變換（Fourier Transform）的第一次偶遇是學習信號與系統的時候，覺得她的數學表達很美，想進一步了解來著，但終究只可遠觀而不能領會其奧義，對她的理解僅僅限于一種數學變換，考試的時候會算算矩形窗的傅里葉變換，按部就班的演算，僅此而已，駕馭不了她，從此形同陌路。

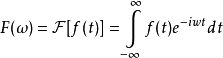
圖1 傅里葉變換，簡潔優雅，貌美如花

轉機出現在學習OFDM(正交頻分復用)的時候，調制與解調是通信的核心部分之一，OFDM的調制與解調卻能用傅里葉變換對如此簡潔而深刻的表述，感嘆不已。傅里葉第一次在我心中有了如此清晰的，初步的物理概念。我一直覺得數學家很厲害，因為任何拋開實際物理概念的數學演繹都是極其抽象的，要想清楚并不容易，數學的抽象與嚴謹而沒有附加物理概念的直觀是我們懼怕數學的重要原因不是嗎。冰冷的數學公式被賦予清晰的物理概念而變得如此鮮活，就如廣義相對論之于黎曼幾何，楊 · 米爾斯規范場之于纖維叢理論。所以呢，了解傅里葉變換的鑰匙就是物理概念。

所謂條條大路通羅馬，不同領域，不同物理或工程角度都給解讀傅里葉變換提供更多可能性，而雷達特別是車載雷達角度的解讀是很有意思的，所以此文嘗試以毫米波雷達視角全面闡述傅里葉變換的物理概念及外延，希望對你有收獲。能夠加深你對她的深刻理解。

在車載雷達應用中，我想很多小伙伴知道對ADC Raw Data做1D FFT，對一維數據做2D FFT，DoA則是3D FFT，如同我們會算rect(t/T)的FT是sinc(w)一樣，但我們可能對其背后的物理概念及外延并不清楚，比如如何理解三個維度都可以做FFT，為什么要做FFT，FFT達不到要求怎么辦，不做FFT行不行等等。如圖2所示公式是單目標MIMO雷達回波表達式，也是當前車載雷達使用最普遍的回波模型之一[1]：

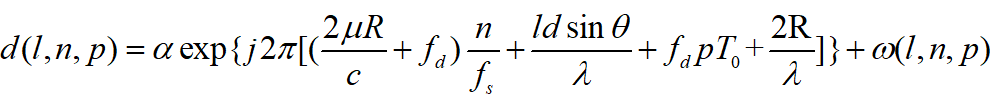
圖2 automotive MIMO Radar 回波表達式（單目標）

它有3個維度，l，n，p，分別代表角度bin，距離bin，速度bin，所以在各自維度的取值范圍內，d(l,n,p)表示一個數據立方體，也叫做radar cube, 如圖3，我們對該cube分別沿range axis, Doppler axis, Space axis做FFT，以提取range, Doppler,以及 Azimuth信息。這是作為雷達算法工程師認識FT的第一層次---知道操作流程，也就是怎么做的問題。

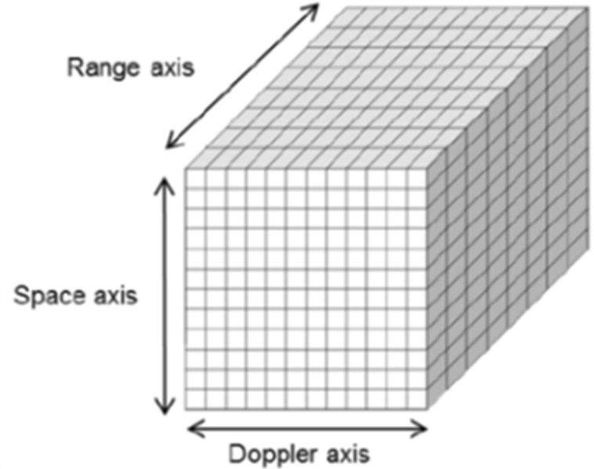
圖3 Radar Cube

接下來我們依次對三個維度中的兩個維度取定值，繼續將d(l,n,p)拆解為3個維度：

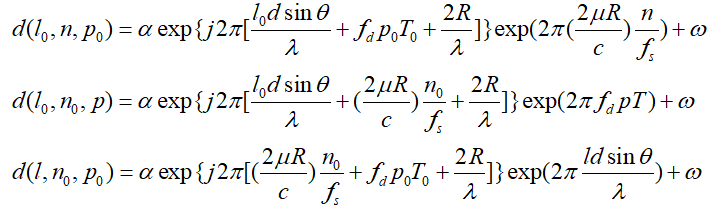
其中高斯白噪聲表達做了簡化，上述3式可以進一步歸納：

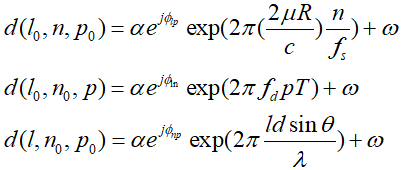
我們發現每個公式開頭其實都是常相位，所以還可以簡化并整理：

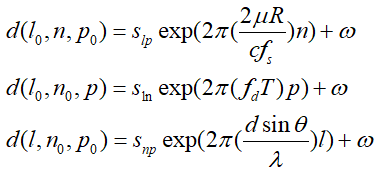
可以看到上述3式的質都是相同的，都具有如下形式：

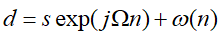
這也是為什么3個維度都可以做FFT的原因。另一方面，我們關心的距離速度方位角信息都包含在一個相對應的頻率之中，信息與頻率是一一對應的，所以信息的獲取轉化為頻率的提取，而FFT就是提取頻率的重要工具。

那么問題又來了，為什么提取頻率的不是其他工具，而是偏偏FFT呢？

繼續分析，實際工程中，我們得到的是d,而d是包含噪聲的，也就是上式中的w。通常，我們假設該噪聲是高斯白噪聲，那么問題又轉化為，高斯白噪聲條件下的頻率估計問題，再來捋一捋，

1 我們有什么，有量測，也就是含噪數據

2 我們假設什么，包含噪聲是高斯白噪聲,也就是知道分布

3 我們要干什么，估計頻率

基于上述1，2，3，我們應該想到似然函數, 上述問題的似然函數為：

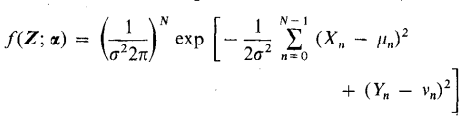
具體推導可以參考文獻[2]，這邊不再贅述，從推導結果來看，高斯白噪聲條件下頻率估計的最大似然結果就是FFT:

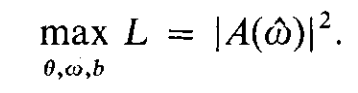
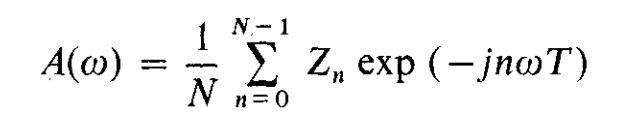
其中L是似然函數，A(w)是FFT，這是認識FT的第二層次--追根溯源，知道為什么要用FFT。應為她在似然準則下估計頻率是最優的。

如前所述，FFT歸根結底還是頻率估計的工具，能不能用其他方法代替呢？回答這個問題取決于你的應用，雷達輸出三個量：距離，速度，角度，而評估這三個量的重要指標是分辨率及精度，根據應用的不同，我們對分辨率及精度的要求是不同的，當然，如果條件允許，當然希望分辨率及精度越高越好。傅里葉變換已經很優秀了，而且還有快速算法的加持，使她在車載雷達等嵌入式平臺獨領風騷，叱咤風云數十載。但我們始終要用發展的，變化的，審視的眼光看問題。是的，那么優秀的FFT也是有瑕疵的：

• 存在瑞利限，分辨率（resolution）不高
• 旁瓣（sidelobe）容易引起虛警(High False Alarms)
• 頻率是時間統計的平均頻率，缺乏時間局部頻率信息
• 多目標條件下，頻率估計精度較差

FFT的瑕疵使得雷達估計那三個量的分辨率及精度較差，也就可能滿足不了你的應用需求。基于此，數十年來，在爭奪頻率估計權力的征途上，各路豪杰層出不窮，好精彩！

傅里葉是分析信號處理的鼻祖，而各個時代的大佬基于前人的工作及自己獨到的見解逐步發展出貝葉斯估計框架，狀態濾波，認知信號處理，以及機器學習或者神經網絡的方法，我們希望在硬件算力及內存允許的條件下，逐步將這些方法用于那3三個量的更好的估計，特別是角度這一塊，這是認識傅里葉的第三個層次--繼往開來，這不是對FFT的否定與拋棄，而是繼承與發展，這些方法也被統稱為現代數字信號處理方法，將會在今后的文章中介紹和分享！

FFT依舊是無窮無盡的寶藏，時常回頭看看她，依舊如沐春風，心生敬畏，如同漂泊異鄉的我們再成功，每每踏上故土，是不是也會感慨萬千：

圖4 讓我再看你一眼，別來無恙