斐波那契

斐波那契（Fibonacci,約1175-1250）出生于比薩，本名Filius Bonacci, 意為波那契的兒子。Fibonacci這個縮寫后的名字，是在1838年才由意大利人利伯里*（Libri, 1803-1869）給取的。利伯里是一位伯爵和數學愛好家，因其對古代珍貴手稿的熱愛和竊書而聞名。

*利布里擔任法國圖書館巡查員期間，偷竊了大量古書，當被發現時，他逃往英國，攜帶著18個大箱，里頭裝著三萬本書和手稿。他在法國被缺席判處10年監禁；一些被盜的作品在他死后被歸還，但仍有許多失散。

不僅如此，斐波那契數列與畢達哥拉斯學派的黃金分割比也有著密切關系。簡而言之，前一項與后一項的比值在項數趨向無窮時的極限為黃金分割比。這個序列除了在數論和許多其他數學分支中常常見到以外，在現代物理、準晶體結構和股票分析等領域都有直接的應用，還可以幫助解決諸如蜜蜂的繁殖、雛菊的花瓣排列、藝術美感和設計諸方面的問題。

斐波那契塑像（1863，比薩營地）

斐波那契家境富裕，他的父親是比薩共和國的政府官員，曾被派往布日伊（Bougie,今屬阿爾及利亞）任商務代理。斐波那契童年時便跟隨父親到了北非，在那里學會了印度-阿拉伯數碼。后來，他又隨父親到過埃及、敘利亞、拜占庭（希臘）、西西里和普羅旺斯等地，通過廣泛深入的學習和研究，他掌握了數學尤其是計算方面的各種技巧。

12世紀末，斐波那契回到比薩，在那里度過了四分之一世紀。他在故鄉著書立說，并在書中采用印度-阿拉伯數碼書寫，促進了這一數碼體系在歐洲的普及。記數和計算則利用巴比倫人發明的60進制，同時他也把數學應用于商業活動的各個領域。斐波那契還闡述了許多代數和幾何問題，其重要成果主要表現在不定分析和數論領域，遠遠超越了前人。

大約在1225年，斐波那契受到神圣羅馬帝國皇帝腓特烈二世的召見，成為宮廷數學家。據說皇帝的隨從向他提出數學問題，被他一一解答。這位皇帝喜歡打仗、美女，也熱愛詩歌和數學，他是歐洲好多位名號為腓特烈二世的君主之一，雖說不是最有名的一個，但他卻擁有多個國王頭銜，按時間順序分別為西西里國王（1197-）、德意志國王（1212-）、神圣羅馬帝國皇帝（1220-）和耶路撒冷國王（1229-）。

腓特烈二世的宮殿自然也有許多處，個人猜測斐波那契是待在西西里王國，那是腓特烈二世度過童年的地方。雖說這位國王有著包括日耳曼等多個民族的血統，但他并不真正喜歡德意志。1224年，腓特烈二世在西西里王國的都城那不勒斯創建了歐洲第一所國立大學（1978年該校以腓特烈二世冠名），其最杰出的畢業生是哲學家托馬斯·阿奎那（Thomas Aquinas，約1225-1274）。事實上，那時在南部意大利，那不勒斯王國與西西里王國是合二為一的。

說到那位天主教世界最重要的哲學家托馬斯·阿奎那，他比斐波那契要年輕一輩。1225年，當斐波那契被國王腓特烈二世召見時，他出生在那不勒斯的洛卡塞卡城堡，那是他家族的領地。16歲那年，他進入那不勒斯大學，后來在巴黎大學獲得神學博士學位。阿奎那的代表作是《神學大全》，翔實地討論了天主教的所有教義。此外，他還給出了上帝存在的五個證明。托馬斯·阿奎那把理性引入神學，同時宣稱：“沒有一種智慧可以不經由感覺而獲得。”

至于斐波那契是否曾在那不勒斯逗留，我們就不得而知了。由于腓特烈二世忙于征戰，以及與控制欲極強的教皇之間的重重矛盾，斐波那契不大可能在這位國王的宮殿里停留太久。事實上，1240年，在他的故鄉比薩留存下來的一份文件上這樣寫道：由于斐波那契曾向市民和官吏講述計算方法，每年給予他薪水若干金幣。換句話說，他有可能在故鄉度過晚年并在那里去世。

斐波那契共有五部著作傳世，包括《花》《平方數書》《算盤書》《實用幾何》和《給帝國哲學家狄奧多魯斯的一封未注明日期的信》。《花》是題獻給腓特烈二世的，書中收入了宮廷里舉行的數學競賽問題。例如，二次方程

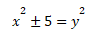
的解。他還證明了，某個三次方程既沒有整數或有理數解，也沒有歐幾里得的無理量解，即用直尺和圓規作出的根。但他卻得到一個小數點后11位數的近似解，無人知道他是如何得到這個結果的。

當然，斐波那契最著名的著作要數《算盤書》（1202）。此處算盤是指用以計算的沙盤，而非真的算盤。書中引進了分數中間的那條橫杠“-”，這是迄今我們仍在使用的符號。還有類似于“百雞問題”的不定方程，那應是受到中國古代數學的影響，這種影響可能是通過阿拉伯人的著作傳遞的。此外，他還講述了求方根的方法和比例變換。不過，最有趣最重要的還是要數“兔子問題”。

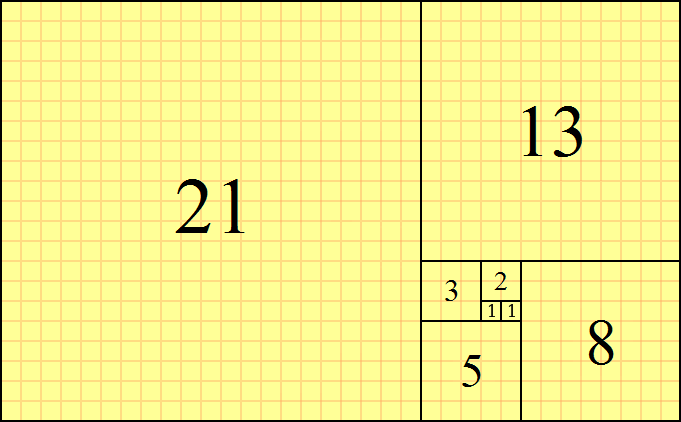
邊長為斐波那契數的正方形折疊

百雞問題與兔子問題

所謂“百雞問題”出現在南北朝時期，在中國北魏數學家張丘建（又叫張邱建）的著作《張丘建算經》中，該書大約成書于公元466-485之間，幸運地流傳至今。其時北魏首都在平城（山西大同），統治者是鮮卑族人。日本古都、六世紀至八世紀的文化藝術中心平城京（奈良）雖是仿長安而建，但其取名應與平城有關。

張丘建的家鄉在清河縣（今屬河北邢臺市），他的算經中最后一道題堪稱亮點，通常被稱為“百雞問題”，民間則流傳著縣令以此考問神童的佳話，原文如下：

今有雞翁一，直錢五；雞母一，直錢三；雞雛三，直錢一。凡百錢買雞百只，問雞翁、母、雛各幾何？

意思是，公雞每只五錢，母雞每只三錢，而雛雞三只才一錢。假設有一百錢，去買一百只雞（錢必須用光），問需買多少只公雞、母雞和雛雞？

設欲購買的公雞、母雞和雛雞的數量分別是x、y、z，此題相當于解下列方程組的正整數解

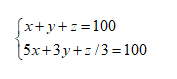
在張丘建時代，中國尚未引進字母，也沒有未知數的概念，用文字敘述這樣的方程組必定是很不容易的。可是，張丘建卻正確地給出了全部三組解答，即（4，18，78），（8，11，81）和（12，4，84）。實際上，他通過消元法，把這兩個三元一次方程化成一個二元一次方程，即

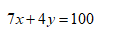
再依次取x為4的倍數，即得上述三組解答。

而所謂“兔子問題”是這樣的：由一對小兔開始，一年后可以繁殖成多少對兔子？其中規定：每對大兔每月能生產一對小兔，而每對小兔兩個月大就成為可以繁殖的大兔。依據“兔子問題”，很容易得到所謂的斐波那契數或斐波那契數列，其前十項是：

1，1，2，3，5，8，13，21，34，55……

這個序列的遞歸公式（數學家發現和定義的第一個遞歸公式）是

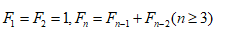
有意思的是，這個數列的通項竟然含有無理數。而前一項與后一項的比值組成的數列竟然存在極限，且這個極限值恰好就是美學中非常重要的黃金分割比。只是，直到四個世紀以后的1611年，這個極限值才由德國天文學家、數學家開普勒（Johannes Kepler,1571-1630）發現，他猜測這個極限就是古希臘的畢達哥拉斯學派定義的黃金分割比，即

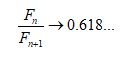
至于這個極限值的證明，至晚在19世紀，才由法國數學家比奈（Jacqttes Binet,1786-1856）給出。

在筆者所著《經典數論的若干問題》中、英文版中，序言的插圖均嚴格依照斐波那契數排列，即第1頁兩幅插圖，第2、3、5、8和13頁各有一幅插圖。在自然界中，斐波那契數列也有意想不到的呈現。以植物界為例，許多花朵的花瓣個數恰好是斐波那契數，例如，梅花5瓣、飛燕草8瓣、萬壽菊13瓣、紫苑21瓣，而雛菊34瓣、55瓣或89瓣的都有。

另外，有一個很有趣的爬樓梯的例子。假設你可以一步登一個臺階，也可以一步登兩個臺階。試問，攀登一個有n個臺階的樓梯有多少種方式？

比較上式和斐波那契數列的定義及其初始值，即可得

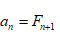
斐波那契數列有許多有趣的性質，它還有一些未解之謎。例如，

是否有無窮多個斐波那契數是素數？

從斐波那契留下來的畫像來看，他的神韻頗似晚他三個世紀的同胞畫家拉斐爾。斐波那契常常以旅行者自居，人們喜歡稱他是“比薩的萊奧拉多”，而把《蒙娜·麗莎》的作者稱為“芬奇的萊奧拉多”。我們可以這么說，斐波那契既是歐洲數學復興的先鋒，也是東西方數學交流的橋梁。

1963年，世界各國一群熱衷研究“兔子問題”的數學家成立了國際性的斐波那契協會，并著手在美國出版《斐波那契季刊》（Fibonacci Quarterly），專門刊登研究與斐波那契數列有關的數學論文。同時，又兩年一度在世界各地輪流舉辦斐波那契數列及其應用國際會議。這在世界數學史上，也可謂是一個奇跡或神話了，堪稱神性的兔子。

相比之下，“百雞問題”只是一個孤立的初等數論問題，沒有可持續研究的內容。

不過，比斐波那契晚20多年出生的中國南宋數學家秦九韶（1202-1261）卻將4世紀《孫子算經》里的“物不知數”問題加以拓廣，推導出了中國剩余定理。至今這個定理仍在許多數學領域有著廣泛的應用，被東西方收錄進每一本初等數論教科書，而按照國際慣例，它應該被稱為秦九韶定理。在2021年出版的拙作《經典數論的現代導引》（中、英文版）中，我們首次將其命名為秦九韶定理。

本文節選自蔡天新著《數學與藝術》，江蘇人民出版社。

作者簡介

蔡天新

浙江大學數學學院教授、博士生導師、求是特聘學者，近作有《歐洲人文地圖》、《美洲人文地圖》、《小回憶》增訂版、《我的大學》、《26城記》、《數學與藝術》、《經典數論的現代導引》（中、英文版）、《完美數與斐波那契序列》（中、英文版），主編《地鐵之詩》、《高鐵之詩》。

編輯：黃飛