混頻器
這是數(shù)學(xué)極客的一個(gè),他們甚至可以提供額外的見(jiàn)解和更正。即使你不是數(shù)學(xué)極客,我相信功能安全領(lǐng)域的每個(gè)人都需要了解這些方程式。在某些時(shí)候,您將不得不調(diào)用其中的一個(gè)或多個(gè)。我將嘗試對(duì)方程有一個(gè)直觀的感覺(jué),所以希望它不會(huì)太糟糕。我確信在我下面的嚴(yán)格數(shù)學(xué)意義上存在錯(cuò)誤,但希望它足夠準(zhǔn)確,可以理解含義并讓您對(duì)這個(gè)主題有良好的感覺(jué)。
此處顯示的方程顯然是針對(duì)隨機(jī)硬件故障的,而不是系統(tǒng)故障模式,因?yàn)槿绻霈F(xiàn)正確的條件,系統(tǒng)故障模式的發(fā)生概率將為 1。
IEC 62308的范圍規(guī)定“本標(biāo)準(zhǔn)描述了項(xiàng)目的可靠性評(píng)估方法。適用于任務(wù)、安全、業(yè)務(wù)關(guān)鍵、高完整性、復(fù)雜電子產(chǎn)品。它包含有關(guān)為什么需要可靠性以及如何以及在何處使用評(píng)估結(jié)果的信息。最后,它詳細(xì)說(shuō)明了如何選擇可靠性評(píng)估方法以及支持評(píng)估所需的數(shù)據(jù)。
所以,讓我們陷入方程(1),它實(shí)際上看起來(lái)最令人生畏。誰(shuí)不喜歡積分和指數(shù)的混合?
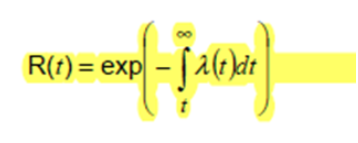
圖2 - 項(xiàng)目隨時(shí)間推移的可靠性的第一個(gè)方程
第一個(gè)等式給出了一個(gè)項(xiàng)目的可靠性,假設(shè)故障率與時(shí)間有關(guān)。在時(shí)間 0 R(t)=1 和時(shí)間 = 無(wú)窮大時(shí),可靠性為 R(t)=0。R(t)可以說(shuō)顯示了可用性,在時(shí)間t仍然存活的設(shè)備比例,這就是為什么積分系數(shù)從t到無(wú)窮大代表所有尚未失效的設(shè)備,這讓我想起了關(guān)于健康只是你可以死亡的最慢速度的笑話。R(t) 的對(duì)正數(shù)是 F(t),表示在時(shí)間 t 之前發(fā)生故障的設(shè)備的比例,然后由 F(t)=1-R(t) 給出,其中“F”代表故障。
λ(t) 表示設(shè)備的故障率,隨著時(shí)間的推移,該故障率可能是恒定的,也可能不是恒定的。對(duì)于功能安全,我們通常假設(shè)λ(t)是一個(gè)常量值λ,所以讓我們這樣做,這使我們能夠簡(jiǎn)化和探索方程。然后我們有 R(t)=exp(-λt),這使得更明顯的是,如果 t=0 R(t)=exp (0) =1 和 t=∞我們有 R(t)=exp(-∞) =0,所以一切都很好。
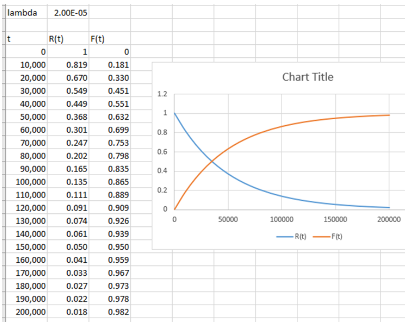
圖 3 - 顯示恒定故障率下大約 20 年內(nèi) R(t) 和 F(t) 形狀的圖
基于它在上述方程中的使用,λ(t) 表示設(shè)備在 t 到 t+dt 區(qū)間內(nèi)發(fā)生故障的幾率,前提是它已經(jīng)存活到時(shí)間 t。它必須存活到時(shí)間t的事實(shí)意味著這被稱為條件概率。條件是它必須幸存到那時(shí)才能在該間隔內(nèi)失敗。
對(duì)于功能安全,dt 通常為 1 小時(shí),因此 λ(8760) 表示設(shè)備在其運(yùn)行第二年的第一個(gè)小時(shí)內(nèi)發(fā)生故障的概率,前提是它設(shè)法運(yùn)行至少 1 年。
說(shuō)明故障率是恒定的,這意味著如果一個(gè)設(shè)備已經(jīng)存活了 1 年,它就有可能在 λ 的下一個(gè)小時(shí)內(nèi)發(fā)生故障,如果一個(gè)設(shè)備已經(jīng)存活了 20 年,它仍然有可能在 λ 的下一個(gè)小時(shí)內(nèi)發(fā)生故障,λ 與它已經(jīng)運(yùn)行了多長(zhǎng)時(shí)間無(wú)關(guān)。
注意 – 對(duì)于功能安全,我們通常對(duì)危險(xiǎn)的未檢測(cè)到故障率比實(shí)際故障率更感興趣。設(shè)備無(wú)法進(jìn)入安全狀態(tài)主要是別人的問(wèn)題。因此 λ 實(shí)際上更有可能是 λD危險(xiǎn)故障率甚至λ的危險(xiǎn)的未檢測(cè)到的故障率。
順便說(shuō)一句,這意味著如果您在 10 年后用相同設(shè)計(jì)的完美新設(shè)備替換完全工作的設(shè)備,您將一無(wú)所獲,因?yàn)樵诮酉聛?lái)的一小時(shí)內(nèi),兩者都會(huì)有 λ 的故障率。
此外,值得提醒的是,如果設(shè)備的故障率為 1e-9/h,這并不意味著它會(huì)持續(xù)十億年。相反,這意味著如果您有十億臺(tái)設(shè)備運(yùn)行 1 小時(shí),您可以預(yù)期其中 1 臺(tái)在該小時(shí)內(nèi)出現(xiàn)故障。同樣,如果您只有 100k 個(gè)單位并且它們運(yùn)行了一年,您可以預(yù)期其中一個(gè)在該年的某個(gè)時(shí)候出現(xiàn)故障。
讓我們繼續(xù)第二個(gè)等式。下面,f(t)顯示為可靠性函數(shù)微分的負(fù)值,對(duì)于恒定故障率,這意味著R(t)具有平滑下降的形狀(見(jiàn)上圖3)。這意味著這種差分的負(fù)值將是正數(shù)(不確定負(fù)失敗率意味著什么)。在嚴(yán)格的數(shù)學(xué)語(yǔ)言中,f(t)是失敗概率密度函數(shù)。它還表示在 t 到 t+dt 區(qū)間內(nèi)無(wú)條件地失效,即不需要存活到時(shí)間 t。與λ(t)相比,即使故障率恒定,1年后f(t)也會(huì)比20年后的f(t)高得多,因?yàn)榇蠖鄶?shù)設(shè)備在此之前就已經(jīng)失效了。當(dāng)它達(dá)到20年時(shí),它必須度過(guò)所有其他年份,因此在接下來(lái)的一個(gè)小時(shí)內(nèi)它仍然失敗的可能性非常小。如果 0.9 是預(yù)計(jì)存活 1 年的設(shè)備比例,如果預(yù)計(jì)在 1 年 + 1 小時(shí)存活的比例為 0.89,則 f(t)= (0.9-0.89)/1=0.01 在 1 年,即 delta R/delta t。從數(shù)學(xué)上看,如下所示。
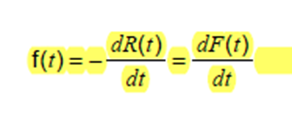
圖 4 - 失效概率密度函數(shù)的第二個(gè)方程
注意 – 快速刷新。要區(qū)分 y=exp(f(x)) 使用 dy/dx = d(f(x)/dx))* exp(f(x))
讓我們以常數(shù)故障率為例,使 R(t)=exp(-λt) 然后 d(R(t))/d(t)= -λexp(-λt) =-λR(t) 這樣 f(t)=λR(t)。由于R(t)=1在時(shí)間0(所有設(shè)備仍然存活)和R(t)=0在時(shí)間無(wú)窮大,那么f(t)從λ到0,其中λ(t)是一個(gè)常數(shù)λ。
下面的第三個(gè)等式是用λ(t)替換λ并重新排列項(xiàng)。
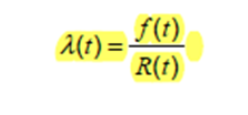
圖 5 - 瞬時(shí)故障率的第三個(gè)公式
下圖顯示了條件失效率 λ(t) 和非條件失效率 f(t),繪制在大約 20 年的時(shí)間內(nèi),常數(shù) λ(t) 為 2e-6/h。理論上,λ(t) 一直恒定到無(wú)窮大,但 f(t) “迅速”下降到零,因?yàn)闆](méi)有設(shè)備會(huì)失效(在概率意義上)。
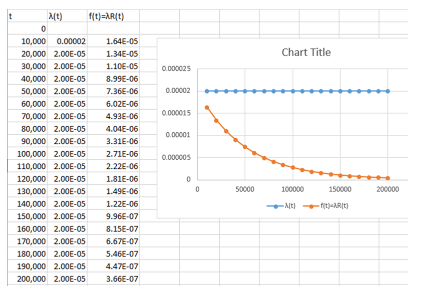
圖 6 有條件和無(wú)條件故障率圖
最后,我們只剩下可靠性和平均故障時(shí)間之間的關(guān)系。查看史密斯的書(shū)以獲得指導(dǎo),請(qǐng)考慮R(t)如下。如果有 N 個(gè)項(xiàng)目,并且 NS(t) 是在時(shí)間 t 時(shí)仍存活的設(shè)備數(shù),則 R(t)=NS(t)/N。
注意 – NS 代表 N琥珀色 S孵化。
假設(shè)我們想知道在所有設(shè)備發(fā)生故障之前,N 個(gè)單元可以預(yù)期運(yùn)行多少小時(shí)。在每個(gè)時(shí)間間隔內(nèi),總運(yùn)行小時(shí)數(shù)增加 NS(t)*dt。因此,總運(yùn)行小時(shí)數(shù)由 NS(t) wrt dt 的 0 到 ∞ 的積分給出。一個(gè)器件的平均預(yù)期時(shí)間為積分除以 N,但 NS(t)/N = R(t) 給出以下等式。
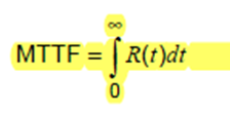
圖 7 - 顯示平均故障時(shí)間的第四個(gè)方程
推導(dǎo)清楚地表明了MTTF實(shí)際上是什么。如果您有 5 臺(tái)設(shè)備,并且它們存活 100 小時(shí)、1000 小時(shí)、2000 小時(shí)、5000 小時(shí)和 10000 小時(shí),則 5 臺(tái)設(shè)備的總運(yùn)行時(shí)間為 18,100 小時(shí),MTTF = 18100/5 = 3620 小時(shí)。
最后,讓我們總結(jié)一下IEC 62308中的方程式,以假設(shè)功能安全中通常發(fā)現(xiàn)的恒定故障率。

圖 8 - 如果 lambda 是常數(shù),則為上述等式
上面沒(méi)有說(shuō)明,但可以從數(shù)學(xué)中得出,如果 MTTF 為 X 并且故障率恒定,那么 63.2% 的項(xiàng)目將在 X 小時(shí)運(yùn)行后出現(xiàn)故障。另外值得說(shuō)明的是,對(duì)于假設(shè)的恒定故障率,1 臺(tái)設(shè)備運(yùn)行 1 萬(wàn)小時(shí)與 1 萬(wàn)臺(tái)設(shè)備運(yùn)行 1 小時(shí)相同。
您還可以以其他方式操作方程式。例如,如果一個(gè)IC的恒定故障率為1000 FIT它能存活20年的機(jī)會(huì)有多大。R(t)=exp(-1e-6*20*8760)=0.84。
希望這個(gè)博客能給你信心,不要害怕圍繞可靠性的數(shù)學(xué)。希望它能讓你能夠嘗試方程式。
審核編輯:郭婷
-
數(shù)據(jù)
+關(guān)注
關(guān)注
8文章
7002瀏覽量
88941 -
效率
+關(guān)注
關(guān)注
0文章
149瀏覽量
20051
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
汽車(chē)功能安全與可靠性的關(guān)系


#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-1
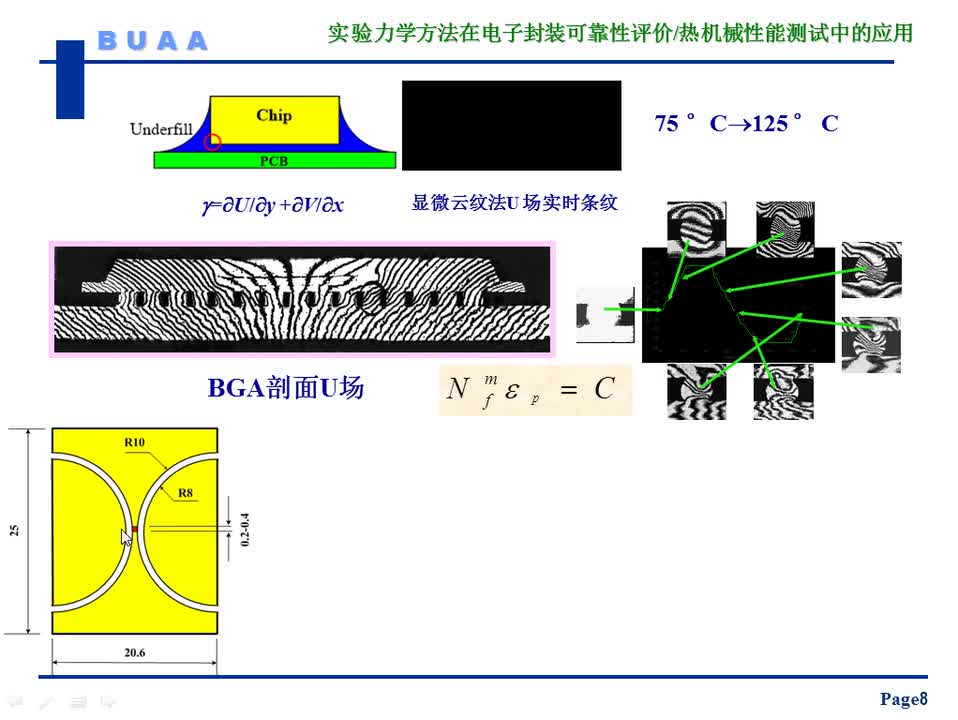
#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-2
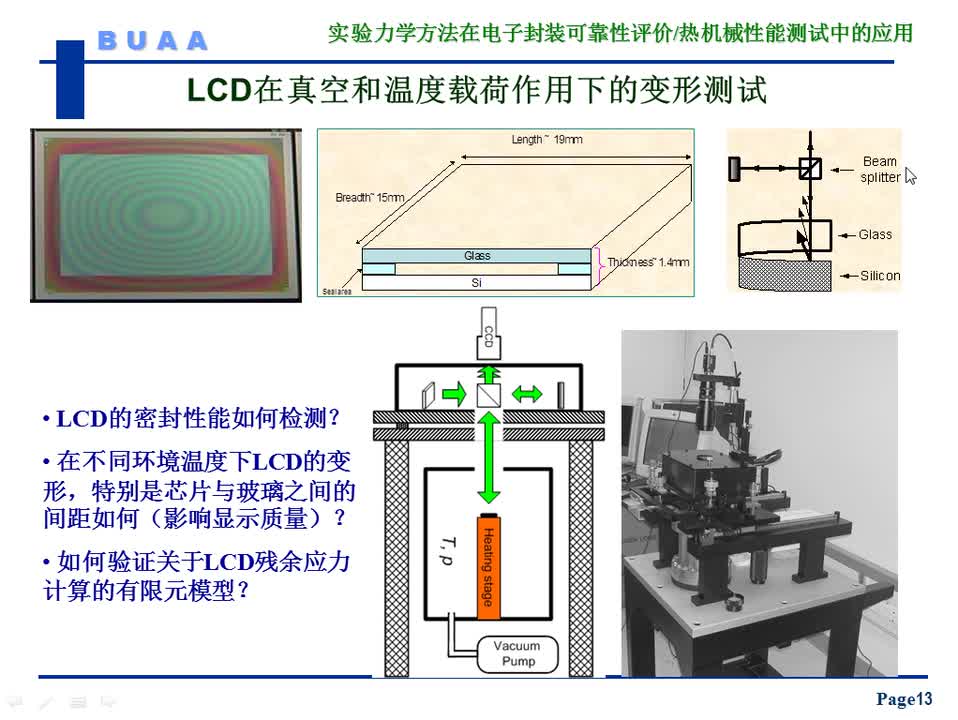
#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-3

#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-4

#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-5
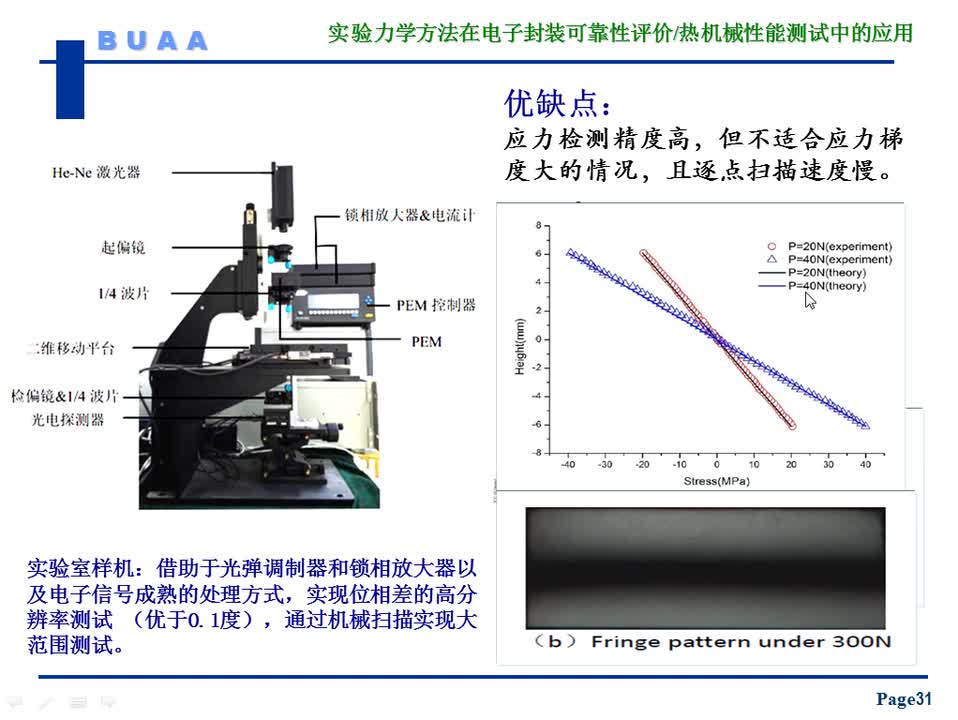
#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-6
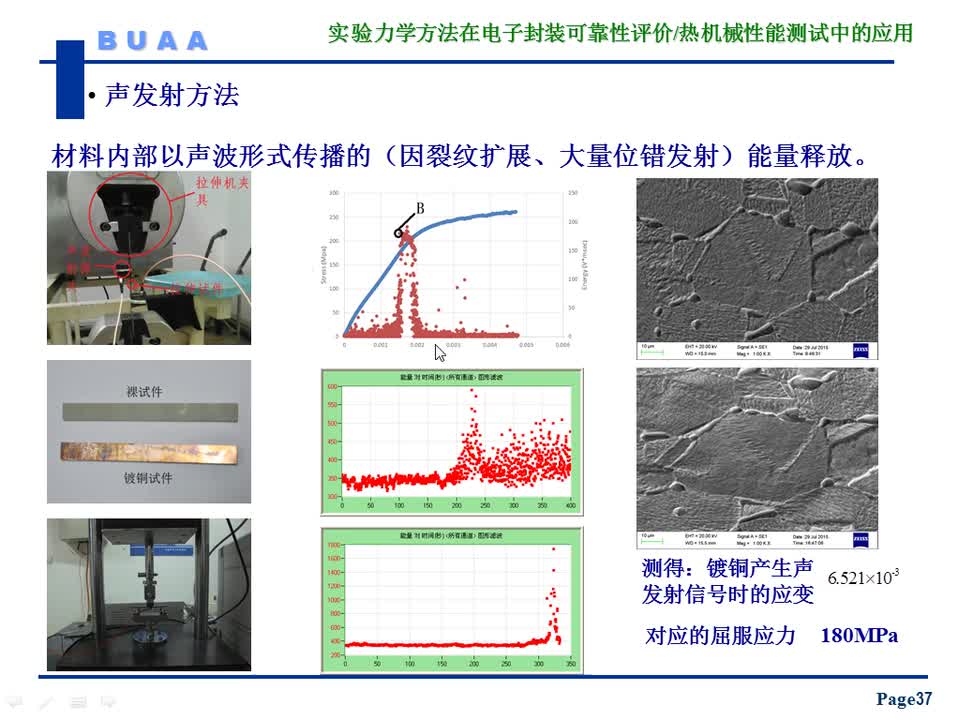
#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-7

#硬聲創(chuàng)作季 #可靠性 電子封裝可靠性評(píng)價(jià)中的實(shí)驗(yàn)力學(xué)方法-8





 功能安全的可靠性方程
功能安全的可靠性方程










評(píng)論