發射機中的本振相噪，是影響發射信號EVM的一個因素。

先來看看理論分析。

首先來看看EVM的定義。

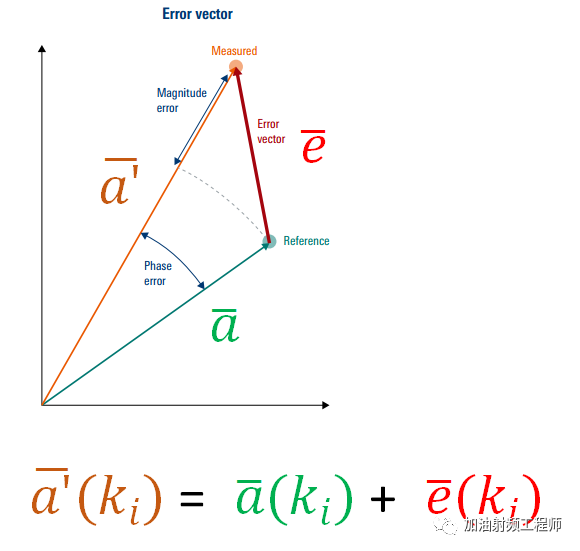
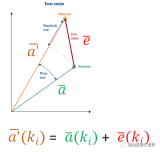
對于每一個符號而言，有一個理論上的位置，即上圖中的綠點(Reference)，但是實際上，符號對應的點，在星座圖上會有偏移，如上圖中的桔黃色的點(Measured)。

而理想和現實之間的差距，即是誤差矢量，如上圖紅色箭頭所示。

由上圖可知，對于每一個符號ki, 誤差矢量可以由下式進行表示：

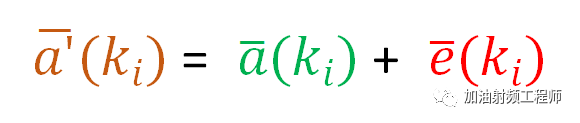
在文獻[1]中，對EVM的定義是這樣的：

我的理解是這樣的，就是，雖然針對單個符號可以計算EVM，但是書中的定義，是基于多個符號對應誤差矢量的平均值。

其數學表達式為：

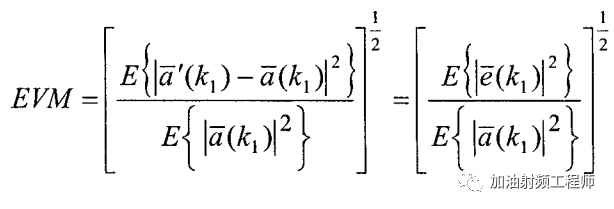
然后再看看怎么把相位噪聲換算到EVM上。

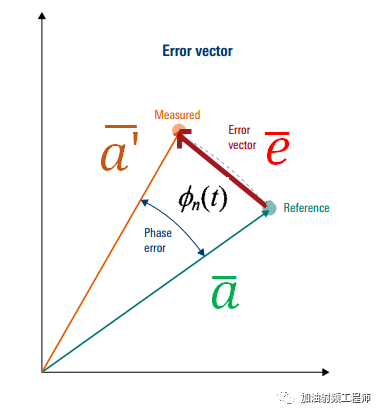
既然，現在只是考慮相位噪聲對EVM的影響，所以可以不考慮幅度誤差。

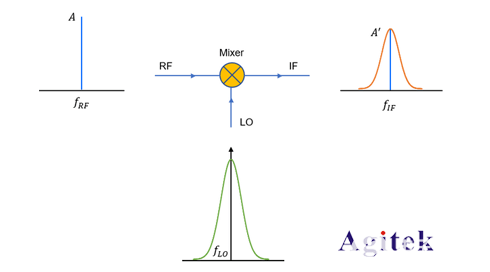
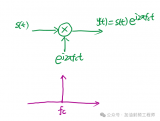
并且，假設上述的矢量誤差，是由于本振的相噪引起的。

本振的相噪，可以看成是一個很小的隨機相位量，定義為：

所以，實測的信號，可以用下式進行表示：

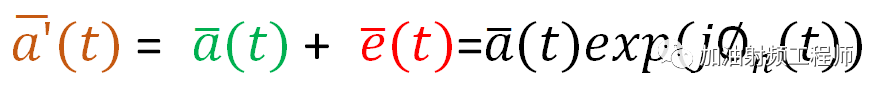
因此，誤差矢量的幅度如下圖所示：

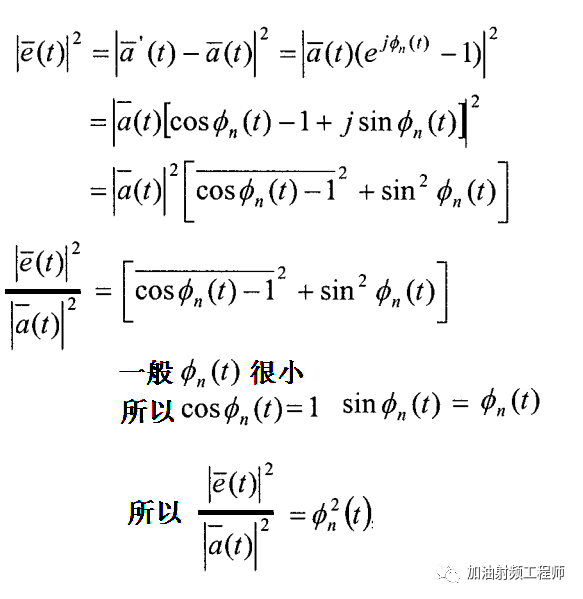
相噪的自相關函數與其對應的功率譜密度有如下的關系(我隨機過程學的不好，所以下面的式子，并不是很理解，先copy過來)。

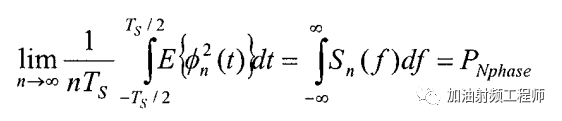
所以（在文獻[1]的基礎上，補了個dt，還有綠圈中為啥又不是Ts了呢？不過可以先看結論）:

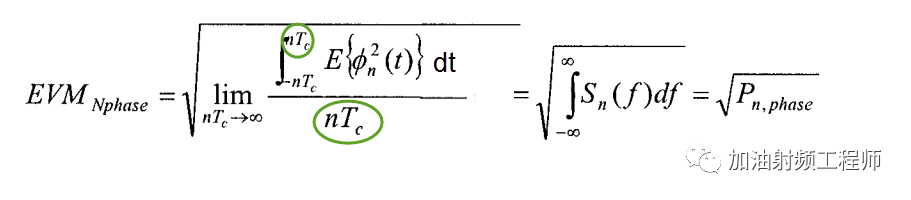
假設本振的環路帶寬相對較寬，則由于相噪累積出來的能量為：

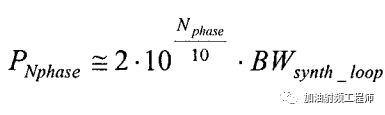
其中，Nphse是平均相噪，單位為dBc/Hz，BWsynth_loop是環路濾波器的帶寬，單位為Hz。

所以，

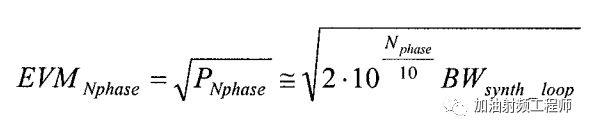
如果使用了多個本振，則

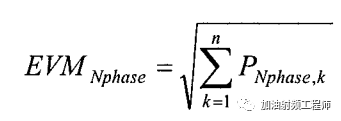
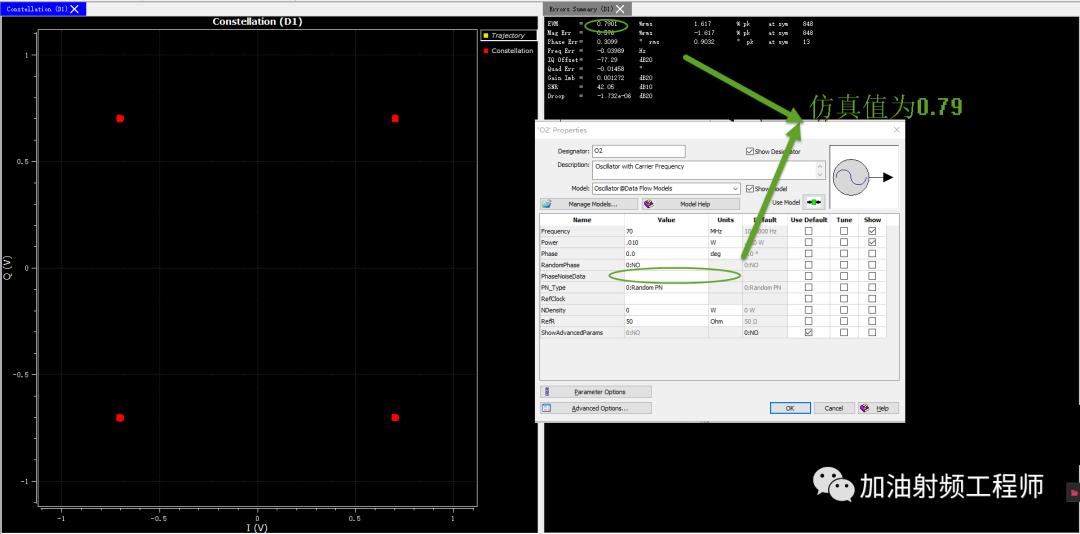
然后再看看仿真驗證。

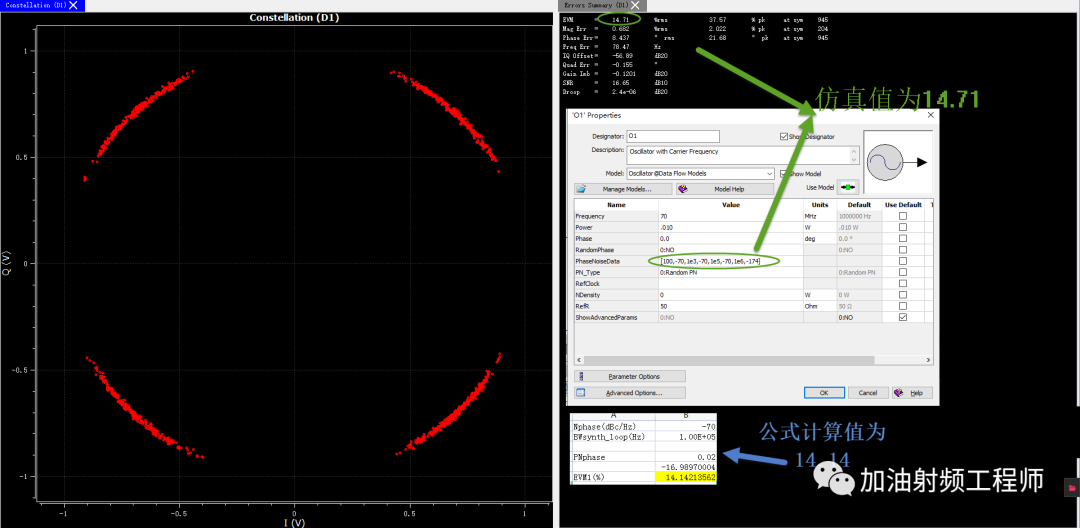
用SystemVue進行驗證，發現當LO不考慮相噪時，EVM為0.79%。

當相噪為:

-70dBc/Hz@100Hz,

-70dBc/Hz@1000Hz

-70dBc/Hz@100KHz

-174dBc/Hz@1MHz

時，仿真得到的值為14.71%，而根據上述公式，計算得到的值為14.14%。兩種結果對比來看，理論公式的預估還是比較準確的。

同時，可以從星座圖中看到，測量點成為一個弧形，這也與開頭的假設相呼應，即沒有幅度誤差或者很小，只有相位誤差。

審核編輯：劉清