假設測試樣本需被分為三類，首先需構建三個支持向量機模型，分別為：

（1）第一個支持向量機模型將樣本分類為類別1和類別2， （2）第二個支持向量機模型將樣本分類為類別1和類別3， （3）第三個支持向量機模型將樣本分類為類別2和類別3。

然后將每個訓練數據輸入至上述三個支持向量機的模型中，并采用“投票”的方式確定每個測試樣本的類別。例如，對于某一測試樣本，若第一個支持向量機模型將該樣本分類至類別1，第二個支持向量機模型將該樣本分類至類別1，第三個支持向量機模型將該樣本分類至類別2，此時，類別1“被投兩票”，類別2“被投一票”，類別3“被投零票”，因此，該樣本最終被分類為得票數最高的類別1。

但上述“投票”方式可能出現“平票”的情況。例如，對于某一測試樣本，若第一個支持向量機模型將該樣本分類至類別1，第二個支持向量機模型將該樣本分類至類別3，第三個支持向量機模型將該樣本分類至類別2。

“平票”情況可導致不能分類問題，1類對另1類的方式可通過將測試樣本在上述三個支持向量機模型中各類別的分數加和，并將該樣本歸類于分數和最大的類別的方式解決上述不能分類的問題。

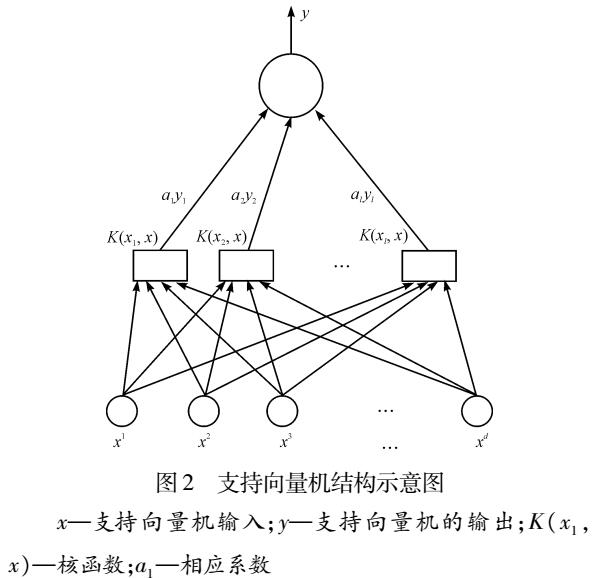
測試樣本所獲得的分數可通過支持向量機判別式計算得出，即： socre=∑αiyiK(Xi,X)+b 例如，對于某一測試樣本，若： 其在第一個支持向量機模型（類別1VS類別2）獲得的分數為0.5， 其在第二個支持向量機模型（類別1VS類別3）獲得的分數為-0.2， 其在第三個支持向量機模型（類別2VS類別3）獲得的分數為0.4。

則該樣本在上述三個支持向量機模型中： 對類別1的分數和為0.5-0.2=0.3， 對類別2的分數和為-0.5+0.4=-0.1， 對類別3的分數和為0.2-0.4=-0.2。 即該樣本對類別1的分數最大，因此該樣本被歸類于類別1。

1類對另1類的方式可解決機器學習相關介紹（20）——支持向量機（多類問題之1類對K-1類方式）中1類對K-1類方式訓練樣本不平衡的問題，但1類對另1類方法需訓練的支持向量機的數量為K(K-1)/2（K為類別數），當K較大時，訓練和測試時間較長。

因此，支持向量機可綜合1類對K-1類和1類對另1類的方式，得出如圖一所示的樹狀方式（下文簡稱“樹狀方式”）。該樹狀方式處理的是一個8分類問題，在處理該問題時，需構建7個分類器（支持向量機模型），每個分類器區分兩個類別。



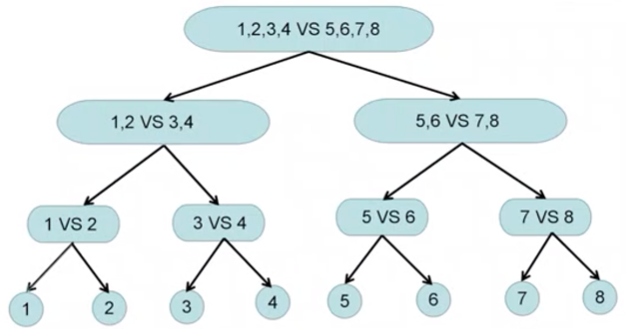
圖一，圖片來源：中國慕課大學《機器學習概論》

該樹狀方式在減少分類器數量的同時兼顧了類別樣本數量的平衡。該樹狀方式需保證每個分類器所區分的兩類差別是顯著的，例如“1、2、3、4VS5、6、7、8”兩類的差別是顯著的。






審核編輯：劉清