作為一名數據科學家,評估機器學習模型性能是您工作的一個關鍵方面。為了有效地做到這一點,您可以使用各種統計指標,每種指標都有自己獨特的優勢和劣勢。通過對這些指標的深入理解,您不僅可以更好地選擇最佳指標來優化模型,還可以向業務利益相關者解釋您的選擇及其影響。
在這篇文章中,我重點討論了用于評估回歸問題的指標,這些回歸問題涉及到預測一個數值,無論是房價還是下個月公司銷售額的預測。由于回歸分析可以被認為是數據科學的基礎,因此理解其中的細微差別至關重要
殘留物快速入門
殘差是大多數度量的構建塊。簡單地說,殘差是實際值和預測值之間的差值
residual = actual - prediction
紅線是機器學習模型的擬合,在這種情況下線性回歸橙色線表示觀測值與該觀測的預測值之間的差異。正如您所看到的,殘差是為樣本中的每個觀測值計算的,無論是訓練集還是測試集。
回歸評估指標
本節討論了一些最流行的回歸評估指標,這些指標可以幫助您評估模型的有效性。
偏見
最簡單的誤差度量是殘差之和,有時被稱為偏差。由于殘差既可以是正的(預測值小于實際值)也可以是負的(預測大于實際值),所以偏差通常會告訴你的預測值是高于還是低于實際值
然而,由于相反符號的殘差相互抵消,您可以獲得一個生成偏差非常低的預測的模型,而該模型根本不準確。
或者,您可以計算平均殘差,或者平均偏誤( MBE )。
R 平方
下一個指標可能是你在學習回歸模型時遇到的第一個指標,尤其是在統計學或計量經濟學課程中。R 平方 ( R 2),也稱為決定系數,表示由模型解釋的方差比例。更準確地說, R 2對應于因變量(目標)的方差可以由自變量(特征)解釋的程度
以下公式用于計算 R 2:
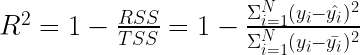
RSS 是殘差平方和,即殘差平方和。此值捕獲模型的預測誤差。
TSS 是平方的總和。為了計算這個值,假設一個簡單的模型,其中每個觀測的預測是所有觀測到的實際值的平均值。 TSS 與因變量的方差成比例,如下所示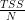 是的實際方差y哪里N是觀測次數.把 TSS 想象成一個簡單的均值模型無法解釋的方差
是的實際方差y哪里N是觀測次數.把 TSS 想象成一個簡單的均值模型無法解釋的方差
實際上,您正在比較模型(由圖 2 中的紅線表示)與簡單平均模型(由綠線表示)的擬合。
知道 R 2的組成部分代表什么,你可以看到 表示您的模型無法解釋的目標中總方差的分數
表示您的模型無法解釋的目標中總方差的分數
在使用 R 2時,需要記住以下幾點。
R 2是一個相對度量;也就是說,它可以用來與在同一數據集上訓練的其他模型進行比較。值越高表示擬合效果越好。
R 2也可以用來粗略估計模型的總體性能。然而,在使用 R 2進行此類評估時要小心:
首先,不同的領域(社會科學、生物學、金融等)認為 R 2的不同值是好是壞。
其次, R 2沒有給出任何偏差的度量,所以你可以有一個 R 2值很高的過擬合(高偏差)模型。因此,您還應該查看其他指標,以更好地了解模型的性能。
R 2的一個潛在缺點是,它假設每個特征都有助于解釋目標的變化,而事實并非總是如此。因此,如果繼續將特征添加到使用普通最小二乘法( OLS )估計的線性模型中, R 2的值可能會增加或保持不變,但永遠不會減少。
為什么?通過設計, OLS 估計使 RSS 最小化。假設一個具有附加特征的模型不能提高第一個模型的 R 2值。在這種情況下, OLS 估計技術將該特征的系數設置為零(或一些統計上不重要的值)。反過來,這會有效地將您帶回初始模型。在最壞的情況下,你可以得到起點的分數。
上一點提到的問題的解決方案是調整后的 R2,它額外懲罰添加對預測目標無用的特征。如果由于添加新功能而導致的 R2 增加不夠顯著,則調整后的 R2 的值會降低。
如果使用 OLS 擬合線性模型,則 R 2的范圍為 0 到 1 。這是因為當使用 OLS 估計(使 RSS 最小化)時,一般屬性是RSS ≤ TSS 。在最壞的情況下, OLS 估計將導致獲得平均模型。在這種情況下, RSS 將等于 TSS ,并導致 R 2的最小值為 0 。另一方面,最好的情況是 RSS = 0 和 R 2= 1 。
在非線性模型的情況下, R 2可能是負的。由于此類模型的模型擬合過程不是基于迭代最小化 RSS ,因此擬合模型的 RSS 可能大于 TSS 。換句話說,該模型的預測比簡單均值模型更適合數據。有關更多信息,請參閱When is R squared negative?
額外的好處:使用 R 2,您可以評估與簡單均值模型相比,您的模型更適合數據。從提高基線模型性能的角度來考慮一個正的 R 2值——類似于技能得分。例如, 40% 的 R 2表示您的模型與基線(即均值模型)相比,均方誤差減少了 40% 。
均方誤差
均方誤差( MSE )是最流行的評估指標之一。如以下公式所示, MSE 與殘差平方和密切相關。不同的是,您現在感興趣的是平均誤差,而不是總誤差。
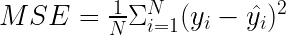
使用 MSE 時需要考慮以下幾點:
MSE 使用平均值(而不是總和)來保持度量與數據集大小無關。
隨著殘差的平方, MSE 對大誤差的懲罰要大得多。其中一些可能是異常值,因此 MSE 對它們的存在并不穩健。
由于度量是用平方、和和常數來表示的 (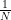 ) ,它是可微的。這對優化算法很有用。
) ,它是可微的。這對優化算法很有用。
在對 MSE 進行優化(將其導數設置為 0 )時,該模型的目標是預測的總和等于實際的總和。也就是說,它導致了平均正確的預測。因此,他們是不偏不倚的。
MSE 不是以原始單位測量的,這可能會使其更難解釋
MSE 是尺度相關度量的一個例子,也就是說,誤差以基礎數據的單位表示(即使它實際上需要一個平方根來以相同的尺度表示)。因此,此類度量不能用于比較不同數據集之間的性能。
均方根誤差
均方根誤差( RMSE )與 MSE 密切相關,因為它只是后者的平方根。取平方將度量帶回目標變量的刻度,這樣更容易解釋和理解。然而,請注意:一個經常被忽視的事實是,盡管 RMSE 與目標的規模相同,但 RMSE 為 10 并不意味著你平均減少了 10 個單位。
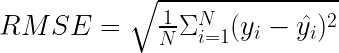
除了規模之外, RMSE 具有與 MSE 相同的屬性。事實上,在訓練模型的同時對 RMSE 進行優化將產生與在對 MSE 進行優化時獲得的模型相同的模型。
平均絕對誤差
要計算的公式平均絕對誤差( MAE )類似于 MSE 公式。將正方形替換為絕對值
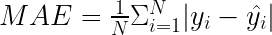
MAE 的特點包括:
由于缺乏平方,度量以與目標變量相同的比例表示,因此更容易解釋
所有誤差都被同等對待,因此度量對異常值是魯棒的。
絕對值忽略了誤差的方向,因此欠填=過填。
與 MSE 和 RMSE 類似, MAE 也依賴于規模,因此無法在不同的數據集之間進行比較。
當您為 MAE 進行優化時,預測值必須比實際值高出許多倍,因為它應該更低。這意味著你正在有效地尋找中位數;也就是說,一個將數據集拆分為兩個相等部分的值
由于公式包含絕對值,因此 MAE 不容易微分。
平均絕對百分比誤差
平均絕對百分比誤差( MAPE )是商業方面最受歡迎的指標之一。這是因為它是以百分比表示的,這使得它更容易理解和解釋。
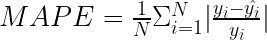
為了使度量更容易閱讀,將其乘以 100% ,以百分比表示數字。
需要考慮的要點:
MAPE 以百分比表示,這使它成為一個與尺度無關的度量。它可以用來比較不同尺度上的預測
MAPE 可以超過 100% 。
當實際值為零時(除以零), MAPE 是未定義的。此外,當實際值非常接近零時,它可以取極值。
MAPE 是不對稱的,對負誤差(當預測高于實際值時)的懲罰比對正誤差的懲罰更重。這是因為對于過低的預測,百分比誤差不能超過 100% 。同時,對于過高的預測沒有上限。因此,對 MAPE 的優化將有利于預測不足而不是預測過度的模型。
Hyndman ( 2021 )闡述了 MAPE 的常見假設;也就是說,變量的測量單位有一個有意義的零值。因此,預測需求和使用 MAPE 不會引發任何危險信號。然而,當預測以攝氏度表示的溫度時,你會遇到這個問題(不僅僅是這個)。這是因為溫度有一個任意的零點,在它們的上下文中談論百分比是沒有意義的。
MAPE 不是處處可微的,這可能會導致在使用它作為優化準則時出現問題。
由于 MAPE 是一個相對度量,相同的誤差可能會導致不同的損失,具體取決于實際值。例如,對于 60 的預測值和 100 的實際值, MAPE 將是 40% 。對于 60 的預測值和 20 的實際值,標稱誤差仍然是 40 ,但在相對尺度上,它是 300% 。
不幸的是, MAPE 并不能提供一種很好的方法來區分重要的和不相關的。假設你正在進行需求預測,在幾個月的時間里,你會得到兩種不同產品 10% 的 MAPE 。然后,事實證明,第一款產品平均每月銷售 100 萬臺,而另一款只有 100 臺。兩者具有相同的 10%MAPE 。當對所有產品進行匯總時,這兩種產品的貢獻是相等的,這可能遠遠不夠理想。在這種情況下,考慮加權 MAPE ( wMAPE )是有意義的。
對稱平均絕對百分比誤差
在討論 MAPE 時,我提到它的一個潛在缺點是它的不對稱性(不限制高于實際值的預測)。對稱平均絕對百分比誤差( sMAPE )是一個試圖解決該問題的相關指標。
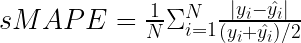
使用 sMAPE 時需要考慮的要點:
它表示為有界百分比,也就是說,它有下限( 0% )和上限( 200% )。
當真實值和預測值都非常接近零時,度量仍然不穩定。當它發生時,你將處理一個非常接近零的數字的除法。
0% 到 200% 的范圍解釋起來并不直觀。分母中的除以二經常被省略。
每當實際值或預測值為 0 時, sMAPE 將自動達到上限值。
sMAPE 包括與 MAPE 相同的關于有意義零值的假設。
在固定無邊界的不對稱性的同時, sMAPE 引入了另一種由公式的分母引起的微妙不對稱性。想象兩個案例。在第一個例子中, A = 100 , F = 120 。 sMAPE 為 18 . 2% 。現在,在類似的情況下,當 a = 100 和 F = 80 時, sMAPE 是 22 . 2% 。因此, sMAPE 傾向于比過度加注更嚴厲地懲罰加注不足。
sMAPE 可能是最具爭議的誤差度量之一,尤其是在時間序列預測中。這是因為文獻中至少有幾個版本的這種度量,每個版本都有輕微的差異,影響其性質。最后,度量的名稱表明不存在不對稱性,但事實并非如此。
需要考慮的其他回歸評估指標
我沒有描述所有可能的回歸評估指標,因為有幾十個(如果不是幾百個的話)。以下是評估模型時需要考慮的其他一些指標:
均方對數誤差( MSLE )是 MSE 的表親,不同之處在于,在計算平方誤差之前,您需要對實際值和預測值進行對數。在減法中取兩個元素的對數,結果是測量實際值和預測值之間的比率或相對差異,而忽略了數據的規模。這就是為什么 MSLE 減少了異常值對最終得分的影響。 MSLE 還加大了對欠充注的懲罰力度
均方根對數誤差( RMSLE )是一個以 MSLE 的平方根為單位的度量。它具有與 MSLE 相同的屬性
Akaike 信息準則( AIC )和貝葉斯信息準則( BIC )是信息標準的例子。它們用于在良好的擬合和模型的復雜性之間找到平衡。如果你從一個簡單的模型開始,添加一些參數,你的模型可能會更好地適應訓練數據。然而,它的復雜性也會增加,并有過度擬合的風險。另一方面,如果從許多參數開始,并系統地刪除其中一些參數,則模型會變得更簡單。同時,您可以降低過擬合的風險,但可能會損失性能(擬合優度)。 AIC 和 BIC 之間的區別在于復雜性懲罰的權重。請記住,將不同數據集甚至同一數據集的子樣本上的信息標準與不同數量的觀測值進行比較是無效的。
何時使用每個評估指標
與大多數數據科學問題一樣,沒有單一的最佳指標來評估回歸模型的性能。為用例選擇的度量將取決于用于訓練模型的數據、您試圖幫助的商業案例等等。因此,您可能經常使用單個度量來訓練模型(為其優化的度量),但在向利益相關者報告時,數據科學家通常會提供一系列度量。
在選擇指標時,請考慮以下幾個問題:
您預計數據集中會出現頻繁的異常值嗎?如果是這樣的話,你想如何解釋它們?
是否存在過度加注或加注不足的商業偏好?
您想要一個與規模相關的度量還是與規模無關的度量?
我認為探索一些玩具箱的指標以充分理解它們的細微差別是有用的。雖然大多數指標在metrics的模塊scikit-learn對于這個特定的任務,好的舊電子表格可能是一個更合適的工具。
以下示例包含五個觀察結果。表 1 顯示了用于計算大多數考慮的度量的實際值、預測和一些度量。
| y | _帽子 | 殘余物 | 平方誤差 | abs 錯誤 | abs perc 錯誤 | sAPE |
| 100 | 120 | -20 | 400 | 20 | 20% | 18 . 18% |
| 100 | 80 | 20 | 400 | 20 | 20% | 22 . 22% |
| 80 | 100 | -20 | 400 | 20 | 25% | 22 . 22% |
| 200 | 240 | -40 | 1 , 600 | 40 | 20% | 18 . 18% |
| 40 | 5 | 35 | 1225 | 35 | 87 . 50% | 155 . 56% |
表 1 。根據五個觀察結果計算性能指標的示例
| 毫秒 | 805 |
| RMSE | 28 . 37 |
| 高級工程師 | 27 |
| 地圖 | 34 . 50% |
| sMAPE | 47 . 27% |
表 2 。使用表 1 中的值計算的性能指標
前三行包含實際值和預測值之間的絕對差為 20 的場景。前兩行顯示了 20 的過量和不足,實際情況相同。第三行顯示了 20 的超額預測,但實際值較小。在這些行中,很容易觀察到 MAPE 和 sMAPE 的特殊性。
表 1 中的第五行包含比實際值小 8x 的預測。為了實驗起見,將預測值替換為比實際值高 8 倍的預測值。表 3 包含修訂后的意見。
| y | _帽子 | 殘余物 | 平方誤差 | abs 錯誤 | abs perc 錯誤 | sAPE |
| 100 | 120 | -20 | 400 | 20 | 20% | 18 . 18% |
| 100 | 80 | 20 | 400 | 20 | 20% | 22 . 22% |
| 80 | 100 | -20 | 400 | 20 | 25% | 22 . 22% |
| 200 | 240 | -40 | 1 , 600 | 40 | 20% | 18 . 18% |
| 40 | 320 | -280 | 78 , 400 | 280 | 700% | 155 . 56% |
表 3 。將單個觀測修改為更極端后的性能指標
| 毫秒 | 16240 |
| RMSE | 127 . 44 |
| 高級工程師 | 76 |
| 地圖 | 157% |
| sMAPE | 47 . 27% |
表 4 。使用表 3 中的修改值計算的性能指標
基本上,所有指標的大小都呈爆炸式增長,這在直覺上是一致的。 sMAPE 的情況并非如此,在兩種情況下都保持不變
我強烈鼓勵您參考這些玩具示例,以便更充分地了解不同類型的場景如何影響評估指標。這個實驗應該讓你更容易決定優化哪個指標以及這種選擇的后果。這些練習也可以幫助你向利益相關者解釋你的選擇。
總結
在這篇文章中,我介紹了一些最流行的回歸評估指標。正如所解釋的,每一個都有自己的優點和缺點。這取決于數據科學家來理解這些,并選擇哪一個(或多個)適合特定的用例。所提到的度量也可以應用于純回歸任務,例如基于與經驗相關的特征選擇來預測工資,也可以應用到時間序列預測領域。
-
NVIDIA
+關注
關注
14文章
4978瀏覽量
102994 -
人工智能
+關注
關注
1791文章
47186瀏覽量
238268 -
機器學習
+關注
關注
66文章
8407瀏覽量
132567
發布評論請先 登錄
相關推薦




 最流行的回歸評估指標
最流行的回歸評估指標











評論