這一篇我們來談其他兩個熱門指標,老生常談的穩定裕量:
增益裕量 Gain Margin,以下簡稱GM
相位裕量 Phase Margin,以下簡稱PM
系統到底有多穩定?
- 系統的時域響應,收斂還是發散→反應 絕對穩定性 (穩定還是不穩定)
- 系統的時域響應,收斂的平穩度→反應 相對穩定性 (穩定裕量有多大)
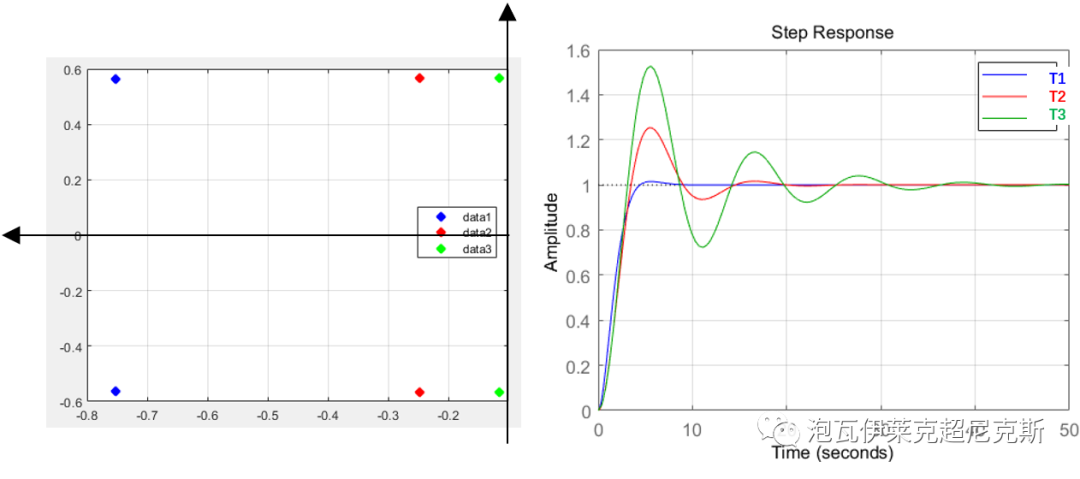
根據勞斯判據,三個閉環典型二階系統T1,T2,T3,如下圖所示,閉環系統特征方程的根都位于左復半平面,因此都是絕對穩定的。
但是,顯然其相對穩定性T1>T2>T3。反應在閉環系統特征方程的根的分布上,即距離虛軸(臨界區域)越遠的,越難振蕩,相對穩定性越好。
換句話說,系統****有多穩定,即相距絕對穩定的臨界區域的距離,有多遠。
波特圖中GM和PM的由來
我們常用開環函數loop gain的頻率特性,來預測和評估閉環系統的性能,因此閉環系統的極點距離臨界區域的距離,得想辦法轉換到開環函數loop gain的頻域指標上,才可以方便地指導設計。這就是導出波特圖中GM和PM的出發點。
為了導出GM和PM,我們必須先回到開環函數loop gain的奈奎斯特圖(Nyquist曲線,即頻域中增益和相角的極坐標,隨頻率變化的軌跡)。
注:引入極坐標和奈奎斯特圖,從而在頻域判斷線性系統的穩定性的原因,可以自行回顧“自動控制原理”勞斯判據,柯西幅角原理,輔助方程和平面映射等基本內容。
奈奎斯特圖和波特圖只是在頻域的不同表現形式:上述三個閉環典型二階系統,其開環函數G1,G2,G3的波特圖(0+→+∞)和奈奎斯特圖(-∞→0-→0+→+∞),兩者對應的關系如下。

注:奈奎斯特曲線總是按照(-∞→0-→0+→+∞→-∞...)這個循環形成包圍曲線,如下所示。

針對工程實際中最常見的開環函數,一般不含有右半平面極點,本身往往是絕對穩定的,只是動態特性欠佳,需要補償和校正。
這樣的開環函數特性,根據奈奎斯特穩定判據,它的奈奎斯特曲線順/逆時針包圍(-1,j0)的正負和要為0,則有如下:
- 結論:
一般/常見的****穩定系統,其閉環函數特征方程的根,在左半平面相距臨界區域(虛軸)的遠近,對應了開環函數loop gain奈奎斯特曲線,相距(-1,j0)這個臨界點的遠近。

以一般/常見形狀的開環系統對應的奈奎斯特圖為例,可以看到,當奈奎斯特曲線通過增益放大或順時針旋轉的方式,都會造成包圍(-1,j0),從而不再滿足奈奎斯特穩定性判據。
為了 達到不穩定的臨界點而允許放大的增益,和允許順時針旋轉的角度,可作為衡量閉環系統相對穩定性高低的指標,即開環函數loop gain的GM和PM 。

PM對動態的影響
真實的工程實踐中,開環函數幾乎都是高階系統。
時域響應波形中我們所關心的形狀和對應頻率段,都可被一個主導二階系統近似。這對主導極點的時域響應,可近似該頻段的時域響應的大致形狀。
故我們仍以典型閉環二階系統的開環函數為例:阻尼比ξ是影響振蕩程度的關鍵參數。從時域響應來看,阻尼比ξ越大,代表系統的穩定性越好。

閉環二階系統中,阻尼比ξ恰可以與開環函數的相位裕量PM對應,直接建立函數關系:


- 結論:
針對典型二階系統主導的閉環系統,其開環函數loop gain的相位裕量:
-
PM≤60°時,阻尼比ξ**≈0.01PM<0.6,PM越低,系統超調越大;**
注:特別的,PM=45°,阻尼比ξ≈0.45,系統超調<20%尚可接受,可作為PM>45°準則的理論支撐。
-
PM>60°時,0.6<阻尼比 ξ <0.01PM ,幾乎不再有超調。
GM對動態的影響
對于GM來說,設計者的初衷并非只針對這一個頻率點,這和上一節所討論的穿越頻率/帶寬的內涵是一致的。
GM設計得大,其本意是希望相位=-180°的高頻之處,以及更高的高頻頻段整體,系統能有足夠大的增益衰減,以抑制環路中的高頻噪聲。
然而,GM和系統其他參數無法解耦, 通過補償器使高頻頻段整體進一步增益衰減,勢必會帶來更多的相位延遲,導致在相對較低的頻率就穿越-180°,從而表現出更小的GM。因此,單獨探討和比較GM的大小,沒有特別的意義。

- 結論:
設計開環函數loop gain的補償器時,應優先保證穿越頻率和PM盡量滿足期望,增益裕量不至過小即可。
-
衰減器
+關注
關注
4文章
640瀏覽量
34373 -
補償器
+關注
關注
0文章
86瀏覽量
14121 -
二階系統
+關注
關注
1文章
16瀏覽量
9596 -
時域響應
+關注
關注
0文章
3瀏覽量
5521
發布評論請先 登錄
相關推薦
LDO的運行困境:低裕量和最小負載
運放相位裕度的認識與理解

解析過沖與相位裕量




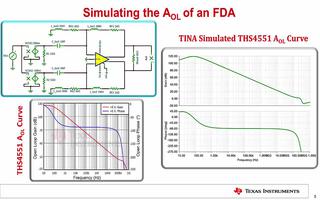
 波特圖中增益裕量GM和相位裕量PM的由來
波特圖中增益裕量GM和相位裕量PM的由來










評論