極市導(dǎo)讀
對煉丹界的當(dāng)紅炸子雞LoRA的「大拷問」!結(jié)合源碼解析深入了解LoRA。>>加入極市CV技術(shù)交流群,走在計(jì)算機(jī)視覺的最前沿
前言
自 ChatGPT 掀起了大模型(LLM)風(fēng)潮后,一大波 LLMs(GPT-4, LLaMa, BLOOM, Alpaca, Vicuna, MPT ..) 百花齊放。知識(shí)問答、文章撰寫、代碼編寫和糾錯(cuò)、報(bào)告策劃等等,它們都會(huì),也能夠交互式地和你玩文字游戲,甚至還有些很有才的朋友將 LLM 作為交互的接口,同時(shí)連接到其它各種模態(tài)(e.g. 視覺 & 語音)的模型,從而創(chuàng)造了炸裂的多模態(tài)效果,炫~!
這么炫,難免人人都想打造一個(gè)自己專屬的 LLM(怎么有種回到了小時(shí)候玩寵物馴養(yǎng)游戲的趕腳..)。但是,大多數(shù)像 CW 這種“平民”玩家,并沒有能夠玩得起 LLM 的資源(主要是 GPU),別說成百上千億參數(shù)量的模型了,就算是幾十億級(jí)別的模型,玩得起的朋友可能也不多。
大多數(shù)人對于 LLM 的“親密度”,可能最多就是拉個(gè)開源的 demo 跑下推理過程,得到個(gè)“意料之中”的結(jié)果,然后很諷刺地自 high 一把:WOW~ 好膩害喲!我們離 AGI 又更近了一步!至于你讓他訓(xùn)一個(gè)?他會(huì)說:呵呵.. 別想太多,洗洗睡吧!
一項(xiàng)技術(shù)通常都不會(huì)在它誕生之初就得以被廣泛使用,和人一樣,它也需要機(jī)遇。正是現(xiàn)在這種背景,加劇了我們大多數(shù)平民在大模型時(shí)代煉丹的矛盾。于是,本文的主角 LoRA(Low-Rank Adaptation of Large Language Models) ,一個(gè)于2021年就出生的家伙,順勢成為煉丹界的當(dāng)紅炸子雞,成功出圈。
本文會(huì)先介紹 LoRA 的概念與優(yōu)勢、講述其 motivation 和 以往方法存在的問題,然后以提問的形式從七個(gè)方面切入去認(rèn)識(shí)與理解 LoRA(結(jié)合源碼解析),接著進(jìn)一步深入思考 LoRA 的一些方面,最后給出一個(gè)應(yīng)用 LoRA 進(jìn)行微調(diào)的例子。對 LoRA 已經(jīng)有基本了解的帥哥靚女們,可以直接跳到“LoRA 七問”與“進(jìn)擊的 LoRA”這兩章。
快給我講講 LoRA 是什么
如今快節(jié)奏生活下的人們都比較浮躁,你們看我吹水那么多水還沒講 LoRA 到底是什么,肯定已經(jīng)饑渴難耐。哦?你說你不會(huì),那很好,CW 為你點(diǎn)贊!不過,我也不磨嘰,該進(jìn)入正題了。
LoRA 的全稱是 "Low-Rank Adaption", 看到 "low-rank",線性代數(shù)玩家們應(yīng)該會(huì)神經(jīng)反射性地聯(lián)系到低秩矩陣。Binggo! 這里就是這個(gè)意思。你問我 LoRA 的中文名?Em.. 就叫它“低秩(自)適應(yīng)”吧,雖然英文里沒有 "self", 但根據(jù) LoRA 的思想和做法及其帶來的效果,它就是自適應(yīng)的意思。
概括地來說,LoRA 是一項(xiàng)主要用于微調(diào) LLMs 的技術(shù),它額外引入了可訓(xùn)練的低秩分解矩陣,同時(shí)固定住預(yù)訓(xùn)練權(quán)重。這個(gè)玩法的重點(diǎn)在于:預(yù)訓(xùn)練權(quán)重不需訓(xùn)練,因此沒有梯度,僅訓(xùn)練低秩矩陣那部分的參數(shù)。
有一點(diǎn) CW 一定要告訴你們:引入的低秩矩陣那部分的參數(shù)量比起預(yù)訓(xùn)練權(quán)重來說,少炒雞多! 這就意味著,比起全量 fine-tune 的玩法,可訓(xùn)練的參數(shù)量少了很多,于是就不需要那么多顯存(GPU)資源了。這對于我等平(貧)民來說,簡直不要太香了~!
利用 LoRA,我們可以享受到諸多福利,比如以下幾點(diǎn):
- 在面對不同的下游任務(wù)時(shí),僅需訓(xùn)練參數(shù)量很少的低秩矩陣,而預(yù)訓(xùn)練權(quán)重可以在這些任務(wù)之間共享;
- 省去了預(yù)訓(xùn)練權(quán)重的梯度和相關(guān)的 optimizer states,大大增加了訓(xùn)練效率并降低了硬件要求;
- 訓(xùn)練好的低秩矩陣可以合并(merge)到預(yù)訓(xùn)練權(quán)重中,多分支結(jié)構(gòu)變?yōu)閱畏种В瑥亩_(dá)到沒有推理延時(shí)的效果;
- 與之前的一些參數(shù)高效的微調(diào)方法(如 Adapter, Prefix-Tuning 等)互不影響,并且可以相互結(jié)合
注:參數(shù)高效的微調(diào)方法 即 PEFT(Parameter-Efficient Fine-Tuning),這類方法僅需微調(diào)少量參數(shù)(可以是額外引入的),而無需微調(diào)預(yù)訓(xùn)練模型的所有參數(shù),從而能夠降低計(jì)算和存儲(chǔ)資源。
靈感來源
對于一項(xiàng)技術(shù),CW 往往會(huì)好奇它是基于怎樣的想法被發(fā)明出來的。也就是,發(fā)明者的靈感來源究竟源自于哪里。可惜無法親自采訪作者,不然我肯定讓他“口若懸河”hhh!沒辦法咯,我只能通過 paper 來為自己找答案。
CW 發(fā)現(xiàn),作者在 paper 中提到:以往的一些工作表明,模型通常是“過參數(shù)化”(over-parametrized)的,它們在優(yōu)化過程中參數(shù)更新的部分通常“駐扎”(reside)在低維子空間中。基于此,作者就順理成章地提出假設(shè):預(yù)訓(xùn)練模型在下游任務(wù)中微調(diào)而更新參數(shù)時(shí),也符合這樣的規(guī)律。
另外,以往的 PEFT 方法存在一系列問題,如:加大了推理延時(shí)、增加了模型深度、限制了輸入句長 等,更重要的是,它們大多數(shù)都打不過全量 fine-tune,也就是最終訓(xùn)完的模型性能沒有全量 fine-tune 來得好。
結(jié)合自己的假設(shè)與時(shí)代背景,作者就搞出了 LoRA,在這種玩法下訓(xùn)出的模型,最終在性能上能和全量 fine-tune 對飆,甚至在一些任務(wù)上還更加出色。
以往的 PEFT 跪在哪里
在上一章,CW 淺淺地提到了以往的 PEFT 方法存在的一些問題,如今在本章,我再稍稍展開來談一下。
在 LoRA 出生之前,比較有代表性的 PEFT 方法主要有額外引入適配下游任務(wù)的 adapter layers 和 優(yōu)化靠近模型輸入層的激活(activations) 兩種。對于后者,比較有代表性的有 prefix tuning 等。其實(shí),降低下要求,這些方法也算是 good 的,畢竟在一定程度上算是 work 了,只是不 good enough ..
對于引入 adapter layers 這類方法,它們的不足在于:
- 新增的 adapter layers 必須串行處理,從而增加了推理延時(shí);
- 在分布式訓(xùn)練時(shí)需要更多的 GPU 同步操作(如 All-Reduce & Broadcast)
至于另一類方法,以 prefix tuning 為例,它們則跪在了:
- 該方法本身很難優(yōu)化;
- 這種方法需要在模型的輸入序列中預(yù)留一部分用作可微調(diào)的 prompt,從而限制了原始輸入文本的句長
LoRA 七問
這一章,CW 會(huì)向大家詳細(xì)說明 LoRA 的玩法,主要從七個(gè)方面切入,分別對應(yīng)以下每一小節(jié)的標(biāo)題,這其實(shí)也是我自己在剛接觸 LoRA 時(shí)所產(chǎn)生的疑問。可以把它們當(dāng)作一個(gè)個(gè) target 去攻破,待全部攻破之后,對 LoRA 應(yīng)該就算是有一定的理解了。
前四節(jié)主要是理論分析,結(jié)合了 paper 中的公式和實(shí)驗(yàn)結(jié)果。后三節(jié)的內(nèi)容則會(huì)結(jié)合源碼解析,這樣會(huì)有更深刻的認(rèn)識(shí)。
為何可以引入低秩矩陣
作者說他之前看到了一篇 paper: Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning,這篇 paper 的結(jié)論是:預(yù)訓(xùn)練語言模型在下游任務(wù)微調(diào)后,權(quán)重矩陣其實(shí)具有很低的 "intrinsic rank"F-。
【關(guān)于 intrinsic rank 的理解】
"intrinsic" 直譯是“內(nèi)在的”、“固有的”,因此我看到有人直接喊 instrinsic rank 為“內(nèi)在秩”、“固有秩”。(⊙o⊙)… 對于這種叫法,我是覺得很別扭,而且有點(diǎn)不明所以。
CW 覺得,在這里,"intrinsic" 應(yīng)該理解為“本質(zhì)上的”、“最具代表性的”會(huì)比較恰當(dāng)。于是,"intrinsic rank" 就應(yīng)當(dāng)理解為最能體現(xiàn)數(shù)據(jù)本質(zhì)的維度(特征)數(shù)目,我們也因此可以美其名曰:“本征秩”。其實(shí),在信號(hào)處理里也有相應(yīng)的概念——intrinsic dimension,它代表能夠表示信號(hào)的最少特征數(shù),它們所對應(yīng)的特征是最能體現(xiàn)信號(hào)本質(zhì)的特征。
也就是說,模型在適配下游任務(wù)后,權(quán)重矩陣的本征秩變得很低,這就代表著其實(shí)并不需要這么高的維度數(shù)就能夠進(jìn)行表征了,在高維度的權(quán)重矩陣中存在冗余。
基于此,作者就自信地認(rèn)為:模型在微調(diào)過程中,權(quán)重更新的那部分(參數(shù)矩陣)肯定也低秩(low rank)的。
Inspired by this, we hypothesize the updates to the weights also have a low “intrinsic rank” during adaptation.
你問:“權(quán)重更新的那部分”具體指什么?
CW 答:模型在微調(diào)過程中,權(quán)重的變化可以表示為 。其中 就是更新前的權(quán)重(在一開始就是預(yù)訓(xùn)練權(quán)重),而 就是更新的那部分,也就是經(jīng)過反向傳播得到梯度后計(jì)算出來的需要更新的量。
LoRA 改變了什么
假設(shè) , 由于梯度與權(quán)重參數(shù)是一對一的, 因此 。如今, 既然認(rèn)為 的本征秩很低,那么不妨對其做低秩分解:
, 其中 , 并且 。
這個(gè) 就是所謂的 low rank,因?yàn)樗h(yuǎn)小于 和 。
由此可知, 經(jīng)過低秩分解后, 這部分的參數(shù)量是遠(yuǎn)小于預(yù)訓(xùn)練權(quán)重 的。
按理來說, 是在反向傳播階段才會(huì)出現(xiàn)的, 但我們可以將其 “提前拿出來” :讓它和 一起做好朋友參與前向過程。這樣一來, 反向傳播時(shí)梯度就只會(huì)傳導(dǎo)到 這部分, 因其本身就是待更新量, 而 初始是預(yù)訓(xùn)練權(quán)重, 被固定了, 無需接收梯度。
經(jīng)過 LoRA 的“洗禮”, 現(xiàn)在如果你喂給模型一個(gè)輸入 , 前向過程就會(huì)表示為:
另外,這里還有兩點(diǎn)需要提一下:
- 低秩矩陣 B,AB,A 的初始化
經(jīng)過 式的低秩分解后, 為了在一開始讓模型的輸出保持為原來預(yù)訓(xùn)練模型的輸出(也就是沒有 那部分), 于是將 初始化為全0, 而 則采用隨機(jī)高斯初始化。
- 對低秩部分的輸出 進(jìn)行 scale
作者在 paper 中還提到, 對于 這部分, 會(huì)乘上一個(gè) scale 系數(shù) 。其中, 相對于 保持一個(gè)常數(shù)倍的關(guān)系。作者認(rèn)為調(diào)節(jié)這個(gè) 大致相當(dāng)于調(diào)節(jié)學(xué)習(xí)率, 于是干脆固定為常數(shù)(這樣就可以偷懶了 )。
降低了哪部分的顯存需求
由于 的參數(shù)量遠(yuǎn)小于 , 因此, 相比于全量 fine-tune 的玩法, LoRA 降低了 optimizer states 這部分對于顯存資源的需求。
這是因?yàn)?optimizer 對于需要更新的模型參數(shù)會(huì)保存一份副本, 在全量 fine-tune 的玩法下, 要全量更新, 于是 optimizer 保存的副本參數(shù)量為 ; 而我們的小可愛 LoRA 僅需更新 這部分, 所以 optimizer 保存的副本參數(shù)量僅為 , 其中 是遠(yuǎn)小于 的。
另外, 我們可能很容易理所當(dāng)然地認(rèn)為 LoRA 對于梯度部分的顯存需求也遠(yuǎn)小于全量 fine-tune, 實(shí)際真的是這樣嗎? 嘿嘿不妨一起來分析下 的梯度是如何計(jì)算的。
假設(shè)模型經(jīng)過如公式 所示的前向過程后得到了輸出 , 并且我們進(jìn)一步計(jì)算出了損失 ,現(xiàn)在我們是來求 的梯度。根據(jù)鏈?zhǔn)角髮?dǎo)法則,易得:
注意 這部分, 它和全量 fine-tune 時(shí)是一樣的, 這部分梯度的 shape 和權(quán)重矩陣的 shape 一致,都是 。
OMG!這就是說, 實(shí)際在計(jì)算 的梯度過程中, 所需的顯存并沒有比全量 fine-tune 來得少, 樣也需要算出 shape 為 的梯度矩陣。更尷尬的是, 由于 的存在, 因此在梯度的計(jì)算過程中, 所需的顯存和計(jì)算量甚至比全量 fine-tune 還來得多.. 幸運(yùn)的是, 在計(jì)算完成后, 這個(gè)中間狀態(tài)量所占的顯存會(huì)被釋放掉, 僅需存儲(chǔ) 這部分 shape 為 的梯度矩陣。
所以說,對于梯度部分,LoRA 在嚴(yán)格意義上并不能降低其對于顯存資源的需求,甚至比起全量 fine-tune 來說計(jì)算量還更大了,只不過降低了最終存儲(chǔ)的需求。
對模型的哪些部分做低秩分解
可是,在如今的 202x 年代,模型通常有 N 個(gè)權(quán)重矩陣,那么應(yīng)該對其中的哪些做低秩分解呢?還是說,應(yīng)該暴力地、一個(gè)不拉地通殺?
對于這個(gè)問題,作者選擇了偷懶,他僅將 LoRA 應(yīng)用于 self-attention 層中的 projection matrices(如),而其中的 MLP 模塊以及 self-attention 層以外的結(jié)構(gòu)均“不受待見”。
In the Transformer architecture, there are four weight matrices in the self-attention module (Wq, Wk, Wv, Wo) and two in the MLP module.
We limit our study to only adapting the attention weights for downstream tasks and freeze the MLP modules.
We leave the empirical investigation of adapting the MLP layers, LayerNorm layers, and biases to a future work.
作者可能也猜到了你們可能會(huì)打破砂鍋問到底:應(yīng)該對 self-attention 層中的哪個(gè)或哪幾個(gè) projection matrices 應(yīng)用 LoRA 呢?于是,對于這個(gè)問題,他倒是下了番功夫去做實(shí)驗(yàn)進(jìn)行探究。
在實(shí)驗(yàn)中,作者以 175B 的 GPT-3 為研究對象,并設(shè)置了參數(shù)量為 18M 的 budget,也就是應(yīng)用了 LoRA 部分的可微調(diào)參數(shù)量不能超過 18M。在這種設(shè)置下,當(dāng)每層僅對 的其中一個(gè)應(yīng)用 LoRA 時(shí),rank 則等于8;而如果每層都對 的其中兩個(gè)應(yīng)用 LoRA,則 rank 等于4。
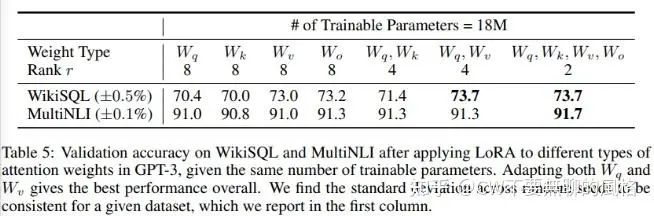
通過上表可以看出,模型更傾向于我們對更多類型的 projection matrices 應(yīng)用 LoRA(如上表顯示,對4個(gè) projection matrices 都應(yīng)用 LoRA 時(shí)效果是最好的),盡管 rank 很低(如上表中最右一列 ), 也足夠讓 捕獲足夠的信息。
在代碼中如何實(shí)現(xiàn)
假設(shè) 是一個(gè)線性層(Linear Layer),我們一起來看看對其應(yīng)用 LoRA 是如何實(shí)現(xiàn)的。
(麻煩認(rèn)真看下代碼中的注釋,謝謝~)
classMergedLinear(nn.Linear,LoraLayer):
#Loraimplementedinadenselayer
def__init__(
self,
in_features:int,
out_features:int,
r:int=0,
lora_alpha:int=1,
lora_dropout:float=0.0,
enable_lora:List[bool]=[False],
fan_in_fan_out:bool=False,
merge_weights:bool=True,
**kwargs,
):
nn.Linear.__init__(self,in_features,out_features,**kwargs)
LoraLayer.__init__(self,r=r,lora_alpha=lora_alpha,lora_dropout=lora_dropout,merge_weights=merge_weights)
# enable_lora 是一個(gè)布爾類型的列表,用于指示對權(quán)重矩陣的哪些“子部分”做低秩分解。
#比如W是shape為(out_features,in_features)的矩陣,
#那么enable_lora=[True,False,True]就表示將W在out_features這個(gè)維度上按序均分成三部分W1,W2,W3,
# shape 均為(out_features // 3, in_features),然后僅對 W1 和 W3 做低秩分解。
#其中 W1 的第一個(gè)維度取值范圍是[0, out_features // 3),W3 則是[2 * out_features // 3, out_features)。
#同理,若 enable_lora =[True],就表示對整個(gè) W 都做低秩分解。
ifout_features%len(enable_lora)!=0:
raiseValueError("Thelengthofenable_loramustdivideout_features")
self.enable_lora=enable_lora
self.fan_in_fan_out=fan_in_fan_out
#Actualtrainableparameters
ifr>0andany(enable_lora):
#僅enable_lora=True的部分應(yīng)用低秩分解,每部分的low-rank是r
self.lora_A=nn.Linear(in_features,r*sum(enable_lora),bias=False)
#注意下這里B是用一維的分組卷積實(shí)現(xiàn)的
self.lora_B=nn.Conv1d(
r*sum(enable_lora),
out_features//len(enable_lora)*sum(enable_lora),
kernel_size=1,
groups=2,
bias=False,
)
#scale系數(shù),對低秩矩陣的輸出(BAx)做縮放
self.scaling=self.lora_alpha/self.r
#Freezingthepre-trainedweightmatrix
#固定住預(yù)訓(xùn)練權(quán)重
self.weight.requires_grad=False
#Computetheindices
#記錄權(quán)重矩陣中,做了低秩分解的是哪些“子矩陣”
self.lora_ind=self.weight.new_zeros((out_features,),dtype=torch.bool).view(len(enable_lora),-1)
self.lora_ind[enable_lora,:]=True
self.lora_ind=self.lora_ind.view(-1)
self.reset_parameters()
iffan_in_fan_out:
#fan_in_fan_out是針對GPT-2的Conv1D模塊的,
#該模塊和Linear的區(qū)別就是維度互為轉(zhuǎn)置
self.weight.data=self.weight.data.T
defreset_parameters(self):
nn.Linear.reset_parameters(self)
ifhasattr(self,"lora_A"):
#initializeAthesamewayasthedefaultfornn.LinearandBtozero
nn.init.kaiming_uniform_(self.lora_A.weight,a=math.sqrt(5))
nn.init.zeros_(self.lora_B.weight)
以上這個(gè)類叫作 MergedLinear, 顧名思義就是低秩分解的部分 可以合并到原來的預(yù)訓(xùn)練權(quán)重 中。
以上代碼中, 比較繞的是與 enable_lora 這個(gè)參數(shù)相關(guān)的內(nèi)容, 該參數(shù)可以用來靈活地指定預(yù)訓(xùn)練權(quán)重 中,哪些部分要做低秩分解。
關(guān)于這個(gè)參數(shù)的設(shè)計(jì)由來, 猜想這是因?yàn)樵谀承┠P偷膶?shí)現(xiàn)中, Attention 層中的 projection matrix 是用一個(gè)共享的線性層實(shí)現(xiàn)的(比如 GPT-2, BLOOM, etc.), 而有了這個(gè) enable_lora 參數(shù), 就可以靈活地指定要對這三者中的哪一個(gè)做低秩分解。
所有需要進(jìn)行低秩分解的層都會(huì)繼承 LoraLayer 這個(gè)父類,這個(gè)類沒有什么特別,也就是設(shè)置一些 LoRA 該有的屬性:
classLoraLayer:
def__init__(
self,
r:int,
lora_alpha:int,
lora_dropout:float,
merge_weights:bool,
):
self.r=r
self.lora_alpha=lora_alpha
#Optionaldropout
iflora_dropout>0.0:
self.lora_dropout=nn.Dropout(p=lora_dropout)
else:
self.lora_dropout=lambdax:x
#Marktheweightasunmerged
#標(biāo)記低秩分解部分是否已經(jīng)合并至預(yù)訓(xùn)練權(quán)重
self.merged=False
#指定是否要將低秩分解部分合并至預(yù)訓(xùn)練權(quán)重中
self.merge_weights=merge_weights
#是否要禁用低秩分解的部分,如果是,則僅使用預(yù)訓(xùn)練權(quán)重部分
self.disable_adapters=False
現(xiàn)在來介紹下 MergedLinear 這個(gè)層的前向過程:
- 先用預(yù)訓(xùn)練權(quán)重 對輸入 實(shí)施前向過程, 得到 ;
- 再將輸入 喂給低秩分解矩陣 , 得到輸出 ;
- 接著對 這部分作 "零填充"使其與 的 shape 一致, 并且進(jìn)行縮放(scale);
- 最后再將這部分的結(jié)果加回至 中, 如前面的公式 。
defforward(self,x:torch.Tensor):
result=F.linear(x,transpose(self.weight,self.fan_in_fan_out),bias=self.bias)
ifself.r>0:
after_A=self.lora_A(self.lora_dropout(x))
after_B=self.lora_B(after_A.transpose(-2,-1)).transpose(-2,-1)
result+=self.zero_pad(after_B)*self.scaling
returnresult
第3點(diǎn)中的“零填充"對應(yīng)以上代碼中的 zero_pad(), 前面 CW 在介紹 enable_lora 這個(gè)參數(shù)時(shí)說過, 由于不一定會(huì)對整個(gè)預(yù)訓(xùn)練權(quán)重矩陣做低秩分解, 于是 的 shape 不一定等同于 , 因此需要對前者進(jìn)行 padding, 使其與后者的 shape 一致, 從而才可讓兩者進(jìn)行 element-wise add 。
現(xiàn)在放出這個(gè)填充的邏輯:
defzero_pad(self,x):
"""將低秩矩陣的輸出BAx與原權(quán)重矩陣輸出Wx在維度上對應(yīng)起來,維度不足的部分用0填充"""
result=x.new_zeros((*x.shape[:-1],self.out_features))
result=result.view(-1,self.out_features)
#將BAx“塞到”與Wx相對應(yīng)的正確位置
result[:,self.lora_ind]=x.reshape(-1,self.out_features//len(self.enable_lora)*sum(self.enable_lora))
returnresult.view((*x.shape[:-1],self.out_features))
怎么做到無推理延時(shí)
CW 在前面提到過,LoRA 的優(yōu)勢之一就是推理無延時(shí)(相比預(yù)訓(xùn)練模型),這是因?yàn)榈椭确纸獾牟糠挚梢院喜⒅猎A(yù)訓(xùn)練權(quán)重中。比如,這時(shí)候模型需要推理,那么你會(huì)先調(diào)用 model.eval(),這時(shí)等同于調(diào)用了 model.train(mode=False),接著再將低秩分解部分合并至預(yù)訓(xùn)練權(quán)重中,過程如下:
deftrain(self,mode:bool=True):
nn.Linear.train(self,mode)
self.lora_A.train(mode)
self.lora_B.train(mode)
#注:當(dāng)調(diào)用 model.eval()時(shí)就會(huì)調(diào)用 train(mode=False)
#將低秩矩陣A,B合并至原權(quán)重矩陣W
ifnotmodeandself.merge_weightsandnotself.merged:
#Mergetheweightsandmarkit
ifself.r>0andany(self.enable_lora):
#delta_W=BA
delta_w=(
#這里使用1維卷積將低秩矩陣 A, B 進(jìn)行“融合”:
# A(r * k)作為輸入,r 看作是其 channel,k 看作是空間維度上的大小;
# B(d * r * 1)作為卷積權(quán)重,d 是 output channel, r 是 input channel, 1 是 kernel size(注意B本身就是用1維分組卷積實(shí)現(xiàn)的)。
#由于是卷積,因此二維的 A 需要增加一維給 mini-batch:r * k -> 1 * r * k。
#卷積后,輸入(1*r*k)->輸出(1*d*k)
F.conv1d(
self.lora_A.weight.data.unsqueeze(0),
self.lora_B.weight.data,
groups=sum(self.enable_lora),
)
.squeeze(0)#1*d*k->d*k
.transpose(-2,-1)#d*k->k*d
)
#zero_pad()是對低秩分解矩陣delta_W進(jìn)行0填充,因?yàn)樵瓩?quán)重矩陣W中可能有些部分沒有進(jìn)行低秩分解,
#從而得到一個(gè)和原權(quán)重矩陣 W 的 shape 對齊的結(jié)果,以便進(jìn)行加和。k * d -> k * D(假設(shè) D 是原權(quán)重矩陣 W 的 out features)
#對于原權(quán)重矩陣 W 是 Linear 層的情況,fan_in_fan_out = False,于是這里會(huì)進(jìn)行 transpose: k * D -> D * k;
#而對于原權(quán)重矩陣W是GPT-2的Conv1D的情況,fan_in_fan_out=True,于是不需要transpose,它的outfeatures就是放在第二維的
#W=W+#delta_W
self.weight.data+=transpose(self.zero_pad(delta_w*self.scaling),notself.fan_in_fan_out)
elifxxx:
...
merge 完之后,在進(jìn)行前向過程時(shí)就無需再像上一節(jié)展示的那樣分步進(jìn)行,而是一步到位(見以下第二個(gè)分支):
defforward(self,x:torch.Tensor):
#此部分先省略,下一節(jié)再介紹
ifxxx:
...
#低秩分解部分已合并
elifself.merged:
returnF.linear(x,transpose(self.weight,self.fan_in_fan_out),bias=self.bias)
#低秩分解部分未合并
else:
result=F.linear(x,transpose(self.weight,self.fan_in_fan_out),bias=self.bias)
ifself.r>0:
after_A=self.lora_A(self.lora_dropout(x))
after_B=self.lora_B(after_A.transpose(-2,-1)).transpose(-2,-1)
result+=self.zero_pad(after_B)*self.scaling
returnresult
如何在下游任務(wù)中靈活地切換
LoRA 還有一點(diǎn)很吸引人,就是模型在某個(gè)下游任務(wù) A 微調(diào)后,可以將低秩矩陣那部分的參數(shù)解耦出來,還原出預(yù)訓(xùn)練權(quán)重,從而繼續(xù)在另一個(gè)下游任務(wù) B 中進(jìn)行微調(diào)。
deftrain(self,mode:bool=True):
nn.Linear.train(self,mode)
self.lora_A.train(mode)
self.lora_B.train(mode)
ifxxx:
...
#前一個(gè)分支是代表mode=False,進(jìn)入該分支說明mode=True,即調(diào)用了model.train(),
#那么當(dāng)?shù)椭染仃?A, B 已經(jīng)合并至原權(quán)重矩陣 W 中時(shí),就需要將它們分解出來,以便進(jìn)行訓(xùn)練(預(yù)訓(xùn)練權(quán)重 W 無需訓(xùn)練)。
elifself.merge_weightsandself.merged:
#Makesurethattheweightsarenotmerged
ifself.r>0andany(self.enable_lora):
#delta_W=BA
delta_w=(
F.conv1d(
self.lora_A.weight.data.unsqueeze(0),
self.lora_B.weight.data,
groups=sum(self.enable_lora),
)
.squeeze(0)
.transpose(-2,-1)
)
#W=W-delta_W
self.weight.data-=transpose(self.zero_pad(delta_w*self.scaling),notself.fan_in_fan_out)
self.merged=False
還原了預(yù)訓(xùn)練權(quán)重后,如果你不想使用低秩矩陣那部分的參數(shù),也可以(見以下第一個(gè)分支):
defforward(self,x:torch.Tensor):
#當(dāng)指定不需要使用adapters部分(在這里即低秩分解矩陣delta_W=BA這部分),
#則將已經(jīng)合并到預(yù)訓(xùn)練權(quán)重W中的delta_W解耦出來,僅用預(yù)訓(xùn)練權(quán)重W對輸入x進(jìn)行前向操作
ifself.disable_adapters:
ifself.r>0andself.mergedandany(self.enable_lora):
delta_w=(
F.conv1d(
self.lora_A.weight.data.unsqueeze(0),
self.lora_B.weight.data,
groups=sum(self.enable_lora),
)
.squeeze(0)
.transpose(-2,-1)
)
#W=W-delta_W
self.weight.data-=transpose(self.zero_pad(delta_w*self.scaling),notself.fan_in_fan_out)
self.merged=False
returnF.linear(x,transpose(self.weight,self.fan_in_fan_out),bias=self.bias)
#當(dāng)使用 adapters 并且低秩分解矩陣delta_W=BA 已經(jīng)合并至預(yù)訓(xùn)練權(quán)重 W 中,則直接進(jìn)行前向過程即可。
elifself.merged:
...
#當(dāng)使用 adapters 但低秩分解矩陣delta_W=BA 未合并到預(yù)訓(xùn)練權(quán)重 W 中,則“分步”進(jìn)行前向過程:
#先用預(yù)訓(xùn)練權(quán)重 W 對輸入 x 實(shí)施前向過程,得到 Wx;
#再將輸入 x 喂給低秩分解矩陣delta_W=BA,得到 adapters 的輸出(delta_W)x;
#接著對 adapters 部分的輸出作零填充使得其與 Wx 的 shape 一致,并且進(jìn)行縮放(scale);
#最后再將這部分的結(jié)果加回至 Wx 中。
else:
...
進(jìn)擊的 LoRA
攻破了 LoRA 七問之后,是時(shí)候來些更深層次的思想活動(dòng)了。
Rank r 的設(shè)置
一個(gè)很直接的問題就是:在實(shí)踐中,rank 應(yīng)該設(shè)為多少比較合適呢?
作者做了幾組實(shí)驗(yàn)進(jìn)行比較,結(jié)果發(fā)現(xiàn) rank 可以很低,不超過8就很 OK 了,甚至是1也挺好..
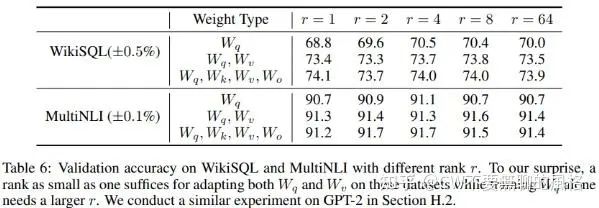
Low Rank 的有效性
看到前面這個(gè)實(shí)驗(yàn)現(xiàn)象,作者“忍不住”認(rèn)為: 擁有很低的本征秩(intrinsic rank),增加 rr 并不能使其覆蓋到更多有意義的子空間,low rank 萬歲!
不過, 他并非是個(gè)嘴炮, 對于這一直覺, 他還是仔仔細(xì)細(xì)地做了個(gè)實(shí)驗(yàn)去驗(yàn)證的。具體做法就是: 以同樣的預(yù)訓(xùn)練模型, 分別用 和 兩種 rank 設(shè)置去應(yīng)用 LoRA 進(jìn)行微調(diào), 然后將訓(xùn)好的低秩矩陣 拿出來做奇異值分解, 得到它們的右奇異單位矩陣 , 最后去比較它們的 top 奇異值向量所張成(span)的子空間的重合程度(使用 Grassmann Distance 度量), 公式表示為(對應(yīng) paper 中的公式4):
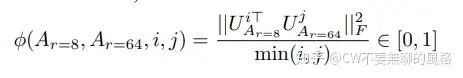
其中 對應(yīng)于 的 top-i 奇異值向量的列, 同理。 的取值范圍是 , 越大代表兩個(gè)子空間重合度越高。

根據(jù)上圖的實(shí)驗(yàn)結(jié)果顯示,兩者在最 top 的那些奇異值向量所張成的空間重合度最高,特別是在 top-1 處,這也對前面一節(jié)“ 效果也不錯(cuò)”提供了一種解釋。
由于在兩種 rank 的設(shè)置下使用的是同一個(gè)預(yù)訓(xùn)練模型,并且經(jīng)過同樣的下游訓(xùn)練后,兩者在 top 奇異值向量的方向上比較一致(其余方向上則相關(guān)度較小),因此這說明 top 奇異值向量所指的方向?qū)τ谙掠稳蝿?wù)i 來說是最有用的,而其它方向可能更多地是一些隨機(jī)噪聲的方向,這可能是訓(xùn)練過程中被潛在地積累下來的。
于是乎,low rank 對于 才是正解。
低秩矩陣與預(yù)訓(xùn)練權(quán)重矩陣的關(guān)系
剛接觸 LoRA 時(shí), CW 就很好奇訓(xùn)出來的這個(gè) 與原來的預(yù)訓(xùn)練權(quán)重 到底有沒有“血緣關(guān)系", 它與 的相關(guān)度是怎么樣的呢?
作者也對這個(gè)問題進(jìn)行了探究, 他將 映射到 的 維子空間, 得到 ,其中 分別是 左、右奇異向量矩陣。然后計(jì)算 的 Frobenius 范數(shù) (后續(xù)簡稱為 范數(shù), 即所有元素的平方和再開方) 。作為對照組, 作者還將 分別映射到了自身和一個(gè)隨機(jī)矩陣的 top-r 奇異值向量空間。

由實(shí)驗(yàn)結(jié)果可以看出, 預(yù)訓(xùn)練權(quán)重矩陣 與低秩矩陣 還算是“近親":比起隨機(jī)矩陣, 映射到 的子空間后的數(shù)值會(huì)大一些。
低秩矩陣的優(yōu)化方向
以上實(shí)驗(yàn)結(jié)果還揭示出兩點(diǎn):
- 低秩矩陣在經(jīng)過下游訓(xùn)練后放大了那些在預(yù)訓(xùn)練時(shí)沒有被強(qiáng)調(diào)的向量方向;
- 對于上一點(diǎn), 較低時(shí)放大程度更強(qiáng) (
咋一看實(shí)驗(yàn)結(jié)果,可能無法 get 到以上第一點(diǎn),那么該如何理解呢?
還是得看回上面那張實(shí)驗(yàn)結(jié)果圖, 無論是 還是 的情況, 映射到 的 維子空間后其 F2 范數(shù)都非常小(0.32 & 1.90), 說明這些子空間的向量方向并非是 中重要程度比較高的方向, 而是在預(yù)訓(xùn)練時(shí)顯得不那么重要的、沒有被強(qiáng)調(diào)的方向。但可以看到, 卻不那么小(6.91 & 3.57), 說明在經(jīng)過下游微調(diào)后, 那些原本存在感不強(qiáng)的方向被重視起來了。
由此可知, 在下游訓(xùn)練過程中, 低秩矩陣 并非簡單地重復(fù)預(yù)訓(xùn)練權(quán)重矩陣的 top 奇異值向量方向,而是去放大原本在預(yù)訓(xùn)練中沒有被強(qiáng)調(diào)的方向。
至于第二點(diǎn), 我們分別在 和 兩種情況下計(jì)算 , 其中 取 那一列的值, 這個(gè)計(jì)算結(jié)果衡量了低秩矩陣在第2點(diǎn)中的放大效應(yīng)。通過計(jì)算, 我們可以發(fā)現(xiàn)在秩比較的低的情況下 放大效應(yīng)更強(qiáng), 那么這又意味著什么呢?
我們有理由認(rèn)為, 低秩矩陣 包含著大部分與下游任務(wù)相關(guān)的向量方向(畢竟是朝著下游最優(yōu)的方向而進(jìn)行優(yōu)化的), 于是以上計(jì)算結(jié)果就意味著適配下游任務(wù)的矩陣的本征秩是低秩的。
巧了! 不小心再次證明了 low rank 對于 才是正解~
低秩是萬能的嗎
CW 在以上多次喊道“l(fā)ow rank 對于 是正解”其實(shí)有點(diǎn)過于夸張了。首先,作者的實(shí)驗(yàn)場景十分有限,沒有在更廣泛的 case 上進(jìn)行驗(yàn)證;其次,我們也不應(yīng)該無腦地認(rèn)為以一個(gè)很小的 值就能夠在所有任務(wù)和數(shù)據(jù)集上 work。
想象下,當(dāng)下游任務(wù)與預(yù)訓(xùn)練任務(wù)的差異(gap)巨大時(shí)(比如在英文上預(yù)訓(xùn)練、而在中文上微調(diào)),使用很小的 值應(yīng)該不會(huì)有好效果,這時(shí)候去微調(diào)模型所有的參數(shù)(可以令 )應(yīng)該會(huì)得到更好的效果,畢竟中英文的向量空間重合度應(yīng)該不那么高,我們需要讓更多的參數(shù)“調(diào)頭”,轉(zhuǎn)向到適配中文的空間中去。
Example: 在單卡 12G 左右的顯存下微調(diào) BLOOM-7B
最后這部分給一個(gè)利用 LoRA 進(jìn)行微調(diào)的例子,這個(gè) demo 基于 Huggingface 的 PEFT 庫,使用了 LoRA + 8bit 訓(xùn)練,其中 8bit 訓(xùn)練需要安裝 bitsandbytes。在單卡的條件下,12G 左右的顯存即可玩起 7B 的 BLOOM。
一些雜碎
先來做一些瑣碎小事:導(dǎo)入模塊、設(shè)置數(shù)據(jù)集相關(guān)參數(shù)、訓(xùn)練參數(shù) 以及 隨機(jī)種子等。
importgc
importos
importsys
importpsutil
importargparse
importthreading
importtorch
importtorch.nnasnn
importnumpyasnp
fromtqdmimporttqdm
fromtorch.utils.dataimportDataLoader
fromdatasetsimportload_dataset
fromaccelerateimportAccelerator
fromtransformersimport(
AutoModelForCausalLM,
AutoTokenizer,
default_data_collator,
get_linear_schedule_with_warmup,
set_seed,
)
frompeftimportLoraConfig,TaskType,get_peft_model,prepare_model_for_int8_training
defset_seed(seed:int):
"""
Helperfunctionforreproduciblebehaviortosettheseedin`random`,`numpy`,`torch`and/or`tf`(ifinstalled).
Args:
seed(`int`):Theseedtoset.
"""
random.seed(seed)
np.random.seed(seed)
ifis_torch_available():
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
#^^safetocallthisfunctionevenifcudaisnotavailable
ifis_tf_available():
tf.random.set_seed(seed)
defmain():
accelerator=Accelerator()
dataset_name="twitter_complaints"
text_column="Tweettext"
label_column="text_label"
#樣本的最大句長
max_length=64
lr=1e-3
batch_size=8
num_epochs=20
#設(shè)置隨機(jī)種子(42yyds!)
seed=42
set_seed(seed)
數(shù)據(jù)加載和預(yù)處理
這里使用的數(shù)據(jù)集是 RAFT(The Real-world Annotated Few-shot Tasks) 任務(wù)中的 Twitter Complaints,有50個(gè)訓(xùn)練樣本和3399個(gè)測試樣本。
下面給出數(shù)據(jù)加載和預(yù)處理的邏輯,代碼本身簡單明了,無需啰嗦。
'''DatsetandDataloader'''
dataset=load_dataset("ought/raft",dataset_name,cache_dir=args.data_cache_dir)
classes=[k.replace("_","")forkindataset["train"].features["Label"].names]
dataset=dataset.map(
lambdax:{"text_label":[classes[label]forlabelinx["Label"]]},
batched=True,
num_proc=4
)
#Preprocessing
tokenizer=AutoTokenizer.from_pretrained(args.model_name_or_path,cache_dir=args.model_cache_dir)
defpreprocess_function(examples):
#注:這里的 batch size 并非訓(xùn)練時(shí)的 batch size,
#在這個(gè)數(shù)據(jù)預(yù)處理的過程中,也是批處理的,所以這里也有個(gè)batchsize的概念
batch_size=len(examples[text_column])
#Addprompt'Label'toinputtext
inputs=[f"{text_column}:{x}Label:"forxinexamples[text_column]]
targets=[str(x)forxinexamples[label_column]]
model_inputs=tokenizer(inputs)
labels=tokenizer(targets)
#依次處理每個(gè)樣本
foriinrange(batch_size):
sample_input_ids=model_inputs["input_ids"][i]
label_input_ids=labels["input_ids"][i]+[tokenizer.pad_token_id]
#將輸入文本(model_inputs)與標(biāo)簽(labels)“對齊”(設(shè)置成一樣),然后將標(biāo)簽中對應(yīng)輸入文本的部分設(shè)為-100,
#這樣在計(jì)算 loss 時(shí)就不會(huì)計(jì)算這部分,僅計(jì)算真實(shí)標(biāo)簽文本的那部分。
#Addlabeltexttoinputtext
model_inputs["input_ids"][i]=sample_input_ids+label_input_ids
#Letthelabelvaluewhichcorrespondtotheinputtextwordtobe-100
labels["input_ids"][i]=[-100]*len(sample_input_ids)+label_input_ids
model_inputs["attention_mask"][i]=[1]*len(model_inputs["input_ids"][i])
#Putpadtokensatthefrontoftheinputs,andtruncateto'max_length'
foriinrange(batch_size):
sample_input_ids=model_inputs["input_ids"][i]
label_input_ids=labels["input_ids"][i]
pad_length=max_length-len(sample_input_ids)
labels["input_ids"][i]=[-100]*pad_length+label_input_ids
model_inputs["input_ids"][i]=[tokenizer.pad_token_id]*pad_length+sample_input_ids
model_inputs["attention_mask"][i]=[0]*pad_length+model_inputs["attention_mask"][i]
#Totensor
model_inputs["input_ids"][i]=torch.tensor(model_inputs["input_ids"][i][:max_length])
model_inputs["attention_mask"][i]=torch.tensor(model_inputs["attention_mask"][i][:max_length])
labels["input_ids"][i]=torch.tensor(labels["input_ids"][i][:max_length])
model_inputs["labels"]=labels["input_ids"]
returnmodel_inputs
deftest_preprocess_function(examples):
batch_size=len(examples[text_column])
inputs=[f"{text_column}:{x}Label:"forxinexamples[text_column]]
model_inputs=tokenizer(inputs)
foriinrange(batch_size):
sample_input_ids=model_inputs["input_ids"][i]
pad_length=max_length-len(sample_input_ids)
model_inputs["input_ids"][i]=[tokenizer.pad_token_id]*pad_length+sample_input_ids
model_inputs["attention_mask"][i]=[0]*pad_length+model_inputs["attention_mask"][i]
#Totensor
model_inputs["input_ids"][i]=torch.tensor(model_inputs["input_ids"][i][:max_length])
model_inputs["attention_mask"][i]=torch.tensor(model_inputs["attention_mask"][i][:max_length])
returnmodel_inputs
withaccelerator.main_process_first():
processed_datasets=dataset.map(
preprocess_function,
batched=True,
num_proc=4,
remove_columns=dataset["train"].column_names,
load_from_cache_file=True,
desc="Runningtokenizerondataset",
)
accelerator.wait_for_everyone()
train_dataset=processed_datasets["train"]
withaccelerator.main_process_first():
processed_datasets=dataset.map(
test_preprocess_function,
batched=True,
num_proc=4,
remove_columns=dataset["train"].column_names,
load_from_cache_file=False,
desc="Runningtokenizerondataset",
)
eval_dataset=processed_datasets["train"]
test_dataset=processed_datasets["test"]
#Dataloaders
train_dataloader=DataLoader(
train_dataset,shuffle=True,collate_fn=default_data_collator,
batch_size=batch_size,pin_memory=True,num_workers=4
)
eval_dataloader=DataLoader(
eval_dataset,collate_fn=default_data_collator,
batch_size=batch_size,pin_memory=True,num_workers=4
)
test_dataloader=DataLoader(
test_dataset,collate_fn=default_data_collator,
batch_size=batch_size,pin_memory=True,num_workers=4
)
print(f"The1sttrainbatchsample:{next(iter(train_dataloader))}
")
Model, Optimizer & Lr scheduler
必備套裝:模型、優(yōu)化器、學(xué)習(xí)率的調(diào)度。
'''Model,Optimizer,LrScheduler'''
#creatingmodel
model=AutoModelForCausalLM.from_pretrained(
args.model_name_or_path,
cache_dir=args.model_cache_dir,
load_in_8bit=args.load_in_8bit,
device_map='auto'#Adevicemapneedstobepassedtorunconvertmodelsintomixed-int8format
)
'''Post-processingonthemodel,includes:
1-Castthelayernorminfp32;
2-makingoutputembeddinglayerrequiregrads;
3-Anablegradientcheckpointingformemoryefficiency;
4-Addtheupcastingofthelmheadtofp32
'''
model=prepare_model_for_int8_training(model)
#配置LoRA的一些參數(shù)
peft_config=LoraConfig(task_type=TaskType.CAUSAL_LM,inference_mode=False,r=8,lora_alpha=32,lora_dropout=0.1)
#對模型應(yīng)用LoRA
model=get_peft_model(model,peft_config)
#打印出可訓(xùn)練的參數(shù)個(gè)數(shù)
model.print_trainable_parameters()
#optimizer
optimizer=torch.optim.AdamW(model.parameters(),lr=args.lr)
#lrscheduler
lr_scheduler=get_linear_schedule_with_warmup(
optimizer=optimizer,
num_warmup_steps=0,
num_training_steps=(len(train_dataloader)*num_epochs),
)
model,train_dataloader,eval_dataloader,test_dataloader,optimizer,lr_scheduler=accelerator.prepare(
model,train_dataloader,eval_dataloader,test_dataloader,optimizer,lr_scheduler
)
accelerator.print(f"Model:{model}
")
Preparation for 8bit Training
這一節(jié)進(jìn)一步解析上一節(jié)中的 model = prepare_model_for_int8_training(model) 這部分,它是為了讓訓(xùn)練過程更穩(wěn)定,以便得到更好的效果,下面來看看其具體做了些什么。
defprepare_model_for_int8_training(
model,output_embedding_layer_name="lm_head",use_gradient_checkpointing=True,layer_norm_names=["layer_norm"]
):
r"""
Thismethodwrappstheentireprotocolforpreparingamodelbeforerunningatraining.Thisincludes:
1-Castthelayernorminfp322-makingoutputembeddinglayerrequiregrads3-Addtheupcastingofthelm
headtofp32
Args:
model,(`transformers.PreTrainedModel`):
Theloadedmodelfrom`transformers`
"""
loaded_in_8bit=getattr(model,"is_loaded_in_8bit",False)
# 1. 固定預(yù)訓(xùn)練的權(quán)重;
#2.將LayerNorm的參數(shù)轉(zhuǎn)換為fp32,這是為了訓(xùn)練的穩(wěn)定性
forname,paraminmodel.named_parameters():
#freezebasemodel'slayers
param.requires_grad=False
ifloaded_in_8bit:
#castlayernorminfp32forstabilityfor8bitmodels
ifparam.ndim==1andany(layer_norm_nameinnameforlayer_norm_nameinlayer_norm_names):
param.data=param.data.to(torch.float32)
#讓Embedding層接受梯度,通過對Embedding層注冊forwardhook實(shí)現(xiàn),
# forward hook 的內(nèi)容會(huì)在模型前向過程完成后被調(diào)用。
#通過以下可以看到,這里hook的內(nèi)容是使Embedding層的輸出接受梯度,
#從而梯度可以傳導(dǎo)到 Embedding 層。
ifloaded_in_8bitanduse_gradient_checkpointing:
#Forbackwardcompatibility
ifhasattr(model,"enable_input_require_grads"):
model.enable_input_require_grads()
else:
defmake_inputs_require_grad(module,input,output):
output.requires_grad_(True)
model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
#enablegradientcheckpointingformemoryefficiency
#對前向過程的中間激活部分的梯度做優(yōu)化,以優(yōu)化內(nèi)存所需。
model.gradient_checkpointing_enable()
#將模型頭部的輸出轉(zhuǎn)換為fp32以穩(wěn)定訓(xùn)練
ifhasattr(model,output_embedding_layer_name):
output_embedding_layer=getattr(model,output_embedding_layer_name)
input_dtype=output_embedding_layer.weight.dtype
classCastOutputToFloat(torch.nn.Sequential):
r"""
Manuallycasttotheexpecteddtypeofthelm_headassometimesthereisafinallayernormthatiscasted
infp32
"""
defforward(self,x):
#這里之所以要先將輸入(x)轉(zhuǎn)換成該層參數(shù)的精度(dtype)是因?yàn)樯弦粚涌赡苁荓ayerNorm,
#而由上可知,我們對LayerNorm的輸出精度轉(zhuǎn)換成了fp32,因此在這種情況下,就需要先將
#上一層的輸出(也就是該層的輸入 x)先轉(zhuǎn)成與該層參數(shù)同樣的精度。
returnsuper().forward(x.to(input_dtype)).to(torch.float32)
setattr(model,output_embedding_layer_name,CastOutputToFloat(output_embedding_layer))
returnmodel
通過以上的源碼實(shí)現(xiàn)并結(jié)合 CW 的注釋,可以知道,這部分主要做了以下四件事情:
- 將 LayerNorm 的參數(shù)轉(zhuǎn)換成 fp32 類型;
- 令 Embedding 層的輸出接收梯度,從而使得梯度得以傳遞至該層;
- 優(yōu)化前向過程產(chǎn)生的中間激活部分的梯度,以減少顯存消耗;
- 將模型頭部(Head)的輸出精度轉(zhuǎn)換成 fp32 類型
PEFT Model
在這一節(jié),CW 引領(lǐng)大家來看看從普通的 model 轉(zhuǎn)換成 peft model:_model = get_peft_model(model, peft_config)_ 是怎么做的,以下針對 BLOOM 模型的情況進(jìn)行解析。
defget_peft_model(model,peft_config):
"""
ReturnsaPeftmodelobjectfromamodelandaconfig.
Args:
model([`transformers.PreTrainedModel`]):Modeltobewrapped.
peft_config([`PeftConfig`]):ConfigurationobjectcontainingtheparametersofthePeftmodel.
"""
model_config=model.config.to_dict()
peft_config.base_model_name_or_path=model.__dict__.get("name_or_path",None)
ifpeft_config.task_typenotinMODEL_TYPE_TO_PEFT_MODEL_MAPPING.keys():
peft_config=_prepare_lora_config(peft_config,model_config)
returnPeftModel(model,peft_config)
ifnotisinstance(peft_config,PromptLearningConfig):
#BLOOM會(huì)進(jìn)入到這個(gè)分支
peft_config=_prepare_lora_config(peft_config,model_config)
else:
peft_config=_prepare_prompt_learning_config(peft_config,model_config)
#在我們這個(gè)例子里,peft_config.task_type是CAUSAL_LM,
#MODEL_TYPE_TO_PEFT_MODEL_MAPPING[peft_config.task_type]則是PeftModelForCausalLM,
#它是PeftModel的子類,它就是在原模型基礎(chǔ)上對目標(biāo)模塊做了LoRA轉(zhuǎn)換的結(jié)果
returnMODEL_TYPE_TO_PEFT_MODEL_MAPPING[peft_config.task_type](model,peft_config)
進(jìn)一步來看看 peft_config = _prepare_lora_config(peft_config, model_config) 這里面的實(shí)現(xiàn),它決定了要對模型的哪些模塊應(yīng)用 LoRA 。
def_prepare_lora_config(peft_config,model_config):
ifpeft_config.target_modulesisNone:
ifmodel_config["model_type"]notinTRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING:
raiseValueError("Pleasespecify`target_modules`in`peft_config`")
#設(shè)置需要進(jìn)行LoRA轉(zhuǎn)換的目標(biāo)模塊,通常是Attention層中的一個(gè)或幾個(gè)映射矩陣(LinearLayer)
#對于BLOOM,這里返回的是["query_key_value"],對應(yīng)的是其模型實(shí)現(xiàn)中BloomAttention中的QKV映射矩陣
peft_config.target_modules=TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING[model_config["model_type"]]
iflen(peft_config.target_modules)==1:
#這個(gè)僅對GPT-2里用到的Conv1D有效
peft_config.fan_in_fan_out=True
#這三個(gè)值分別代表Q,K,V映射矩陣是否要應(yīng)用LoRA
#對于 BLOOM 來說,這里僅對 Q, V 的映射矩陣做轉(zhuǎn)換,而 K 不做。
peft_config.enable_lora=[True,False,True]
ifpeft_config.inference_mode:
#如果是推理模式,則將低秩矩陣A,B合并到Linear層原來的權(quán)重W中
peft_config.merge_weights=True
returnpeft_config
結(jié)合 CW 在上面代碼中的注釋可知,對于 BLOOM,peft_config.target_modules是 ["query_key_value"],這對應(yīng)的是其子模塊 BloomAttention 中的 Q, K, V 映射矩陣:
classBloomAttention(nn.Module):
def__init__(self,config:BloomConfig):
super().__init__()
#省略部分
...
self.hidden_size=config.hidden_size
self.num_heads=config.n_head
self.head_dim=self.hidden_size//self.num_heads
self.split_size=self.hidden_size
self.hidden_dropout=config.hidden_dropout
#省略部分
...
#["query_key_value"]指的就是這個(gè)模塊
self.query_key_value=nn.Linear(self.hidden_size,3*self.hidden_size,bias=True)
self.dense=nn.Linear(self.hidden_size,self.hidden_size)
self.attention_dropout=nn.Dropout(config.attention_dropout)
這個(gè) target_modules 也支持自定義,只要和模型實(shí)現(xiàn)里的關(guān)鍵字匹配得上就行。
訓(xùn)練
其實(shí)就是常規(guī)的訓(xùn)練迭代,只不過這里的特色是利用了 TorchTracemalloc 上下文管理器,它可以方便地計(jì)算出 GPU 和 CPU 的消耗(以 MB 計(jì))。
forepochinrange(num_epochs):
withTorchTracemalloc()astracemalloc:
model.train()
total_loss=0
forstep,batchinenumerate(tqdm(train_dataloader)):
#Forward
outputs=model(**batch)
loss=outputs.loss
total_loss+=loss.detach().float()
#Backward
accelerator.backward(loss)
optimizer.step()
lr_scheduler.step()
optimizer.zero_grad()
ifstep%3==0:
accelerator.print(f"epoch{epoch+1} step{step+1} loss{loss.item()}")
epoch_loss=total_loss/len(train_dataloader)
epoch_ppl=torch.exp(epoch_loss)
accelerator.print(f"[Epoch{epoch+1}] totalloss:{epoch_loss} perplexity:{epoch_ppl}
")
#PrintingtheGPUmemoryusagedetailssuchasallocatedmemory,peakmemory,andtotalmemoryusage
accelerator.print("GPUMemorybeforeenteringthetrain:{}".format(b2mb(tracemalloc.begin)))
accelerator.print("GPUMemoryconsumedattheendofthetrain(end-begin):{}".format(tracemalloc.used))
accelerator.print("GPUPeakMemoryconsumedduringthetrain(max-begin):{}".format(tracemalloc.peaked))
accelerator.print(
"GPUTotalPeakMemoryconsumedduringthetrain(max):{}
".format(
tracemalloc.peaked+b2mb(tracemalloc.begin)
)
)
accelerator.print("CPUMemorybeforeenteringthetrain:{}".format(b2mb(tracemalloc.cpu_begin)))
accelerator.print("CPUMemoryconsumedattheendofthetrain(end-begin):{}".format(tracemalloc.cpu_used))
accelerator.print("CPUPeakMemoryconsumedduringthetrain(max-begin):{}".format(tracemalloc.cpu_peaked))
accelerator.print(
"CPUTotalPeakMemoryconsumedduringthetrain(max):{}
".format(
tracemalloc.cpu_peaked+b2mb(tracemalloc.cpu_begin)
)
)
train_epoch_loss=total_loss/len(eval_dataloader)
train_ppl=torch.exp(train_epoch_loss)
accelerator.print(f"{epoch=}:{train_ppl=}{train_epoch_loss=}
")
順便秀一波訓(xùn)練期間 GPU 和 CPU 的資源消耗情況(以下單位均為 MB):
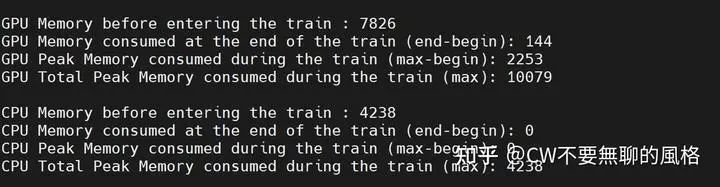
某個(gè) epoch 的訓(xùn)練資源消耗
哦?你說你好奇 TorchTracemalloc 是如何實(shí)現(xiàn)的?OK,CW 也不吝嗇,這就為您獻(xiàn)上:
defb2mb(x):
"""ConvertingBytestoMegabytes."""
returnint(x/2**20)
classTorchTracemalloc:
"""Thiscontextmanagerisusedtotrackthepeakmemoryusageoftheprocess."""
def__enter__(self):
gc.collect()
torch.cuda.empty_cache()
#Resetthepeakgaugetozero
torch.cuda.reset_max_memory_allocated()
#返回當(dāng)前的顯存占用
self.begin=torch.cuda.memory_allocated()
self.process=psutil.Process()
self.cpu_begin=self.cpu_mem_used()
self.peak_monitoring=True
peak_monitor_thread=threading.Thread(target=self.peak_monitor_func)
peak_monitor_thread.daemon=True
peak_monitor_thread.start()
returnself
defcpu_mem_used(self):
"""Getresidentsetsizememoryforthecurrentprocess"""
returnself.process.memory_info().rss
defpeak_monitor_func(self):
self.cpu_peak=-1
whileTrue:
self.cpu_peak=max(self.cpu_mem_used(),self.cpu_peak)
#can'tsleeporwillnotcatchthepeakright(thiscommentishereonpurpose)
#time.sleep(0.001)#1msec
ifnotself.peak_monitoring:
break
def__exit__(self,*exc):
self.peak_monitoring=False
gc.collect()
torch.cuda.empty_cache()
self.end=torch.cuda.memory_allocated()
self.peak=torch.cuda.max_memory_allocated()
self.used=b2mb(self.end-self.begin)
self.peaked=b2mb(self.peak-self.begin)
self.cpu_end=self.cpu_mem_used()
self.cpu_used=b2mb(self.cpu_end-self.cpu_begin)
self.cpu_peaked=b2mb(self.cpu_peak-self.cpu_begin)
評(píng)估
評(píng)估與訓(xùn)練的玩法基本類似,只不過前向過程需要調(diào)用的是模型的 generate() 方法,而非 forward(),前者是 auto-regressive 的方式。
model.eval()
eval_preds=[]
withTorchTracemalloc()astracemalloc:
forbatchintqdm(eval_dataloader):
batch={k:vfork,vinbatch.items()ifk!="labels"}
withtorch.no_grad():
#注:推理過程用的是 auto-regressive 的方式,調(diào)用的是模型的 generate()方法
outputs=accelerator.unwrap_model(model).generate(**batch,max_new_tokens=10)
outputs=accelerator.pad_across_processes(outputs,dim=1,pad_index=tokenizer.pad_token_id)
preds=accelerator.gather(outputs)
#Thepartbefore'max_length'belongstoprompts
preds=preds[:,max_length:].detach().cpu().numpy()
#'skip_special_tokens=True'willignorethosesspecialtokens(e.g.padtoken)
eval_preds.extend(tokenizer.batch_decode(preds,skip_special_tokens=True))
#PrintingtheGPUmemoryusagedetailssuchasallocatedmemory,peakmemory,andtotalmemoryusage
accelerator.print("GPUMemorybeforeenteringtheeval:{}".format(b2mb(tracemalloc.begin)))
accelerator.print("GPUMemoryconsumedattheendoftheeval(end-begin):{}".format(tracemalloc.used))
accelerator.print("GPUPeakMemoryconsumedduringtheeval(max-begin):{}".format(tracemalloc.peaked))
accelerator.print(
"GPUTotalPeakMemoryconsumedduringtheeval(max):{}
".format(
tracemalloc.peaked+b2mb(tracemalloc.begin)
)
)
accelerator.print("CPUMemorybeforeenteringtheeval:{}".format(b2mb(tracemalloc.cpu_begin)))
accelerator.print("CPUMemoryconsumedattheendoftheeval(end-begin):{}".format(tracemalloc.cpu_used))
accelerator.print("CPUPeakMemoryconsumedduringtheeval(max-begin):{}".format(tracemalloc.cpu_peaked))
accelerator.print(
"CPUTotalPeakMemoryconsumedduringtheeval(max):{}
".format(
tracemalloc.cpu_peaked+b2mb(tracemalloc.cpu_begin)
)
)
assertlen(eval_preds)==len(dataset["train"][label_column]),
f"{len(eval_preds)}!={len(dataset['train'][label_column])}"
correct=total=0
forpred,trueinzip(eval_preds,dataset["train"][label_column]):
ifpred.strip()==true.strip():
correct+=1
total+=1
accuracy=correct/total*100
accelerator.print(f"{accuracy=}
")
accelerator.print(f"Predofthefirst10samples:
{eval_preds[:10]=}
")
accelerator.print(f"Truthofthefirst10samples:
{dataset['train'][label_column][:10]=}
")
推理期間,GPU 和 CPU 的消耗情況如下(以下單位均為 MB):
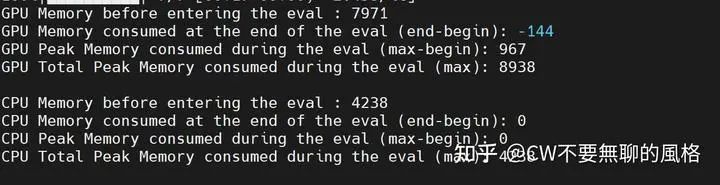
某個(gè) epoch 訓(xùn)練后,推理的資源消耗
End
LoRA 作為當(dāng)今大模型時(shí)代最火的技術(shù)之一,是否算得上是微調(diào) LLMs 的正確姿勢由你們決定。比起正確與否,合不合適才是最重要的。于我而言,只是覺得它好玩而不是無聊的風(fēng)格而已~
-
模型
+關(guān)注
關(guān)注
1文章
3477瀏覽量
49922 -
LoRa
+關(guān)注
關(guān)注
351文章
1756瀏覽量
234182 -
ChatGPT
+關(guān)注
關(guān)注
29文章
1586瀏覽量
8756 -
LLM
+關(guān)注
關(guān)注
1文章
318瀏覽量
668
原文標(biāo)題:當(dāng)紅炸子雞 LoRA,是當(dāng)代微調(diào) LLMs 的正確姿勢?
文章出處:【微信號(hào):GiantPandaCV,微信公眾號(hào):GiantPandaCV】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評(píng)論請先 登錄
氮化鎵助力快充小型化,KEMET聚合物鉭電容大顯身手!
請問UCOS III環(huán)境下正確的調(diào)試姿勢是怎樣的?
淺析人機(jī)界面互動(dòng)技術(shù)的趨勢發(fā)展
小米、華為等當(dāng)紅炸子雞存在的缺點(diǎn),看完再?zèng)Q定入不入手
這款傳感器鞋墊可以告訴你搬重物時(shí)的正確姿勢,免受背部損傷
未來屬于哪種led
成立3年估值23億美金,這家企業(yè)掘金工業(yè)互聯(lián)網(wǎng)的秘訣到底是什么?
騰訊云:組織架構(gòu)調(diào)整告一段落,接下來怎么打仗?
人工智能硬件仍有機(jī)會(huì)制定新標(biāo)準(zhǔn)
OSPF是如何計(jì)算路由的?OSPF如何適應(yīng)大型網(wǎng)絡(luò)的?
5G RedCap緣何成為“當(dāng)紅炸子雞”?
全球首家王者榮耀I(xiàn)P電競酒店!洲明光顯助力打造數(shù)字文娛“潮”空間



















評(píng)論