1，空間矢量

什么是空間矢量呢？

定義：在電機內，可將在空間按正弦分布的量表示為空間矢量。

1.1定子磁動勢空間矢量

啥叫磁動勢？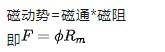

我們知道磁通是有方向的，那么磁動勢當然也是有方向的。這應該沒毛病吧。

那么定子產生的磁場方向如何呢？

如下圖，給繞組通電，根據右手定則 會產生如圖所示磁場。

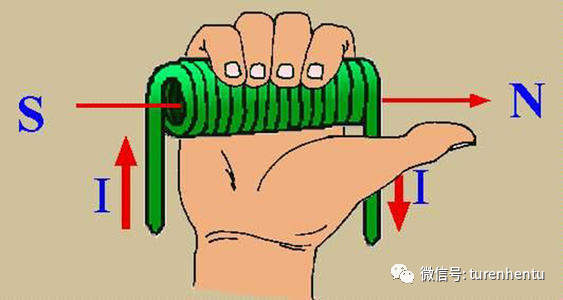
Fig 1 電流產生磁場

推而廣之，如下圖：

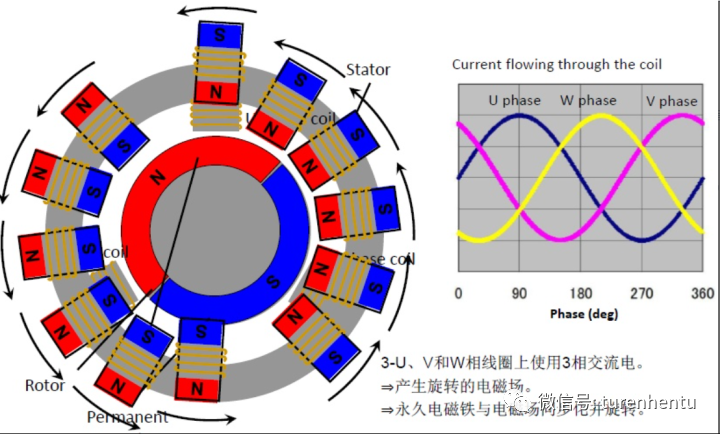
Fig2 電流產生磁場(盜用一張圖，如有侵權，請聯系我刪除)

由Fig2可知，可將通入交變電流的定子繞組等效為一個個小磁鐵。這些磁鐵的磁場方向當然是非常明確的，那么在某個瞬間其合成磁場也應該是明確的。按一定順序使定子繞組導通，便產生了沿圓周方向不斷運動的定子合成磁場，從而拖動永磁體轉子沿一個方向不斷運動（異性相吸原理）。

當我們按照上圖這樣想的時候，其實磁動勢空間矢量的概念呼之欲出啊。而磁動勢為什么沿空間正弦分布呢？可以簡單地歸結為，和電機設計內容相關（比如定子繞組的分布方式等）。

所有繞組，最終可以簡化為，位于a,b,c三相軸線上的三個線圈，通入電流后，會產生與實際相繞組等同的磁動勢。如下圖，圖中ia/ib/ic為各相電流的正方向。

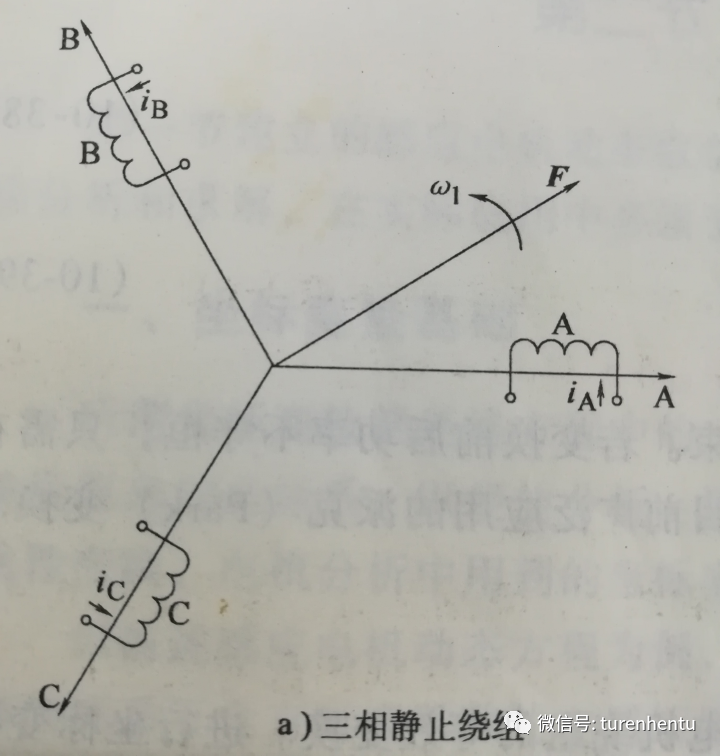
Fig3 等效繞組形式

可知，a/b/c三相各自產生的磁動勢空間矢量和各相軸線方向平行(根據電流方向取與軸線方向相同或者相反)。

為了助于理解，放一張磁鏈空間矢量動圖：

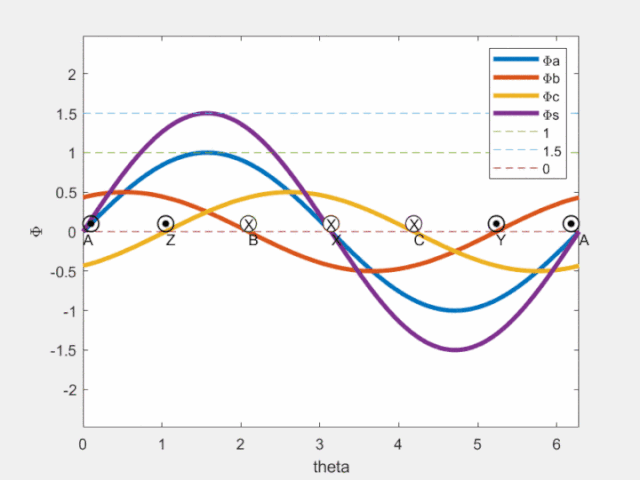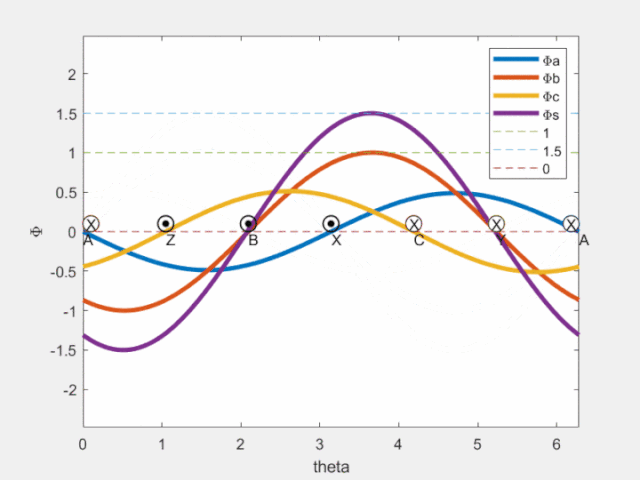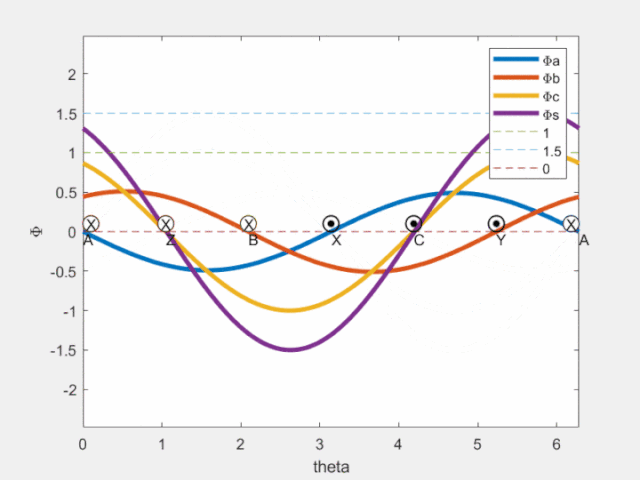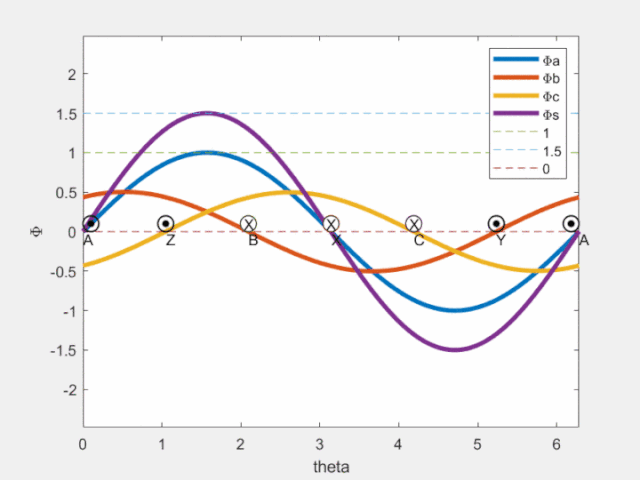
Fig4 磁鏈空間矢量

由上圖可見，a/b/c各相產生的磁鏈在該相軸線處脈動；圖中紫色曲線為合成磁鏈空間矢量，可知其在空間按正弦分布，且沿圓周旋轉（旋轉磁場，轉一周，即可獲得理想磁鏈圓）。

是不是證明了這么一句話：在電機氣隙內，定子磁場按正弦分布。

1.2 電流空間矢量

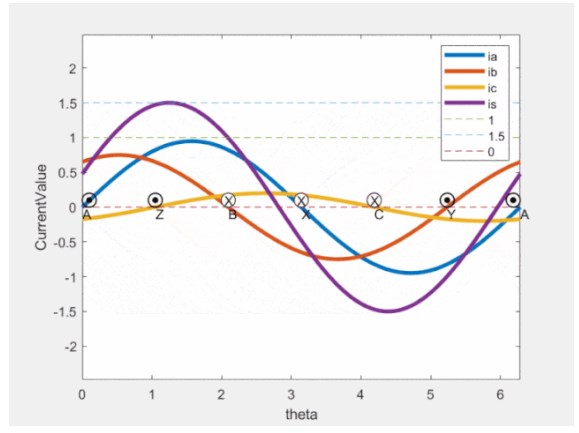
Fig 5 電流空間矢量

其中：

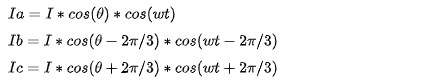
上述公式組中的第二個cos很好理解，表征通入的三相正弦電流，大小隨時間變化；上述公式組中的第一個cos，可能會讓新手有點蒙圈。前面提到了，其實這個cos的根源和定子繞組的處理方式有關（分布繞組/短距繞組可以讓繞組合成磁動勢更加接近正弦）。

從圖上可見，a/b/c三相電流在空間按正弦分布，且在軸線方向來回脈振，但其合成電流空間矢量Is卻繞圓周不斷旋轉。

如果將上圖中電流乘以K再除以磁阻呢?就得到Fig 4 中磁鏈空間矢量。

電流空間矢量概念存在的前提是，必須將之和磁動勢空間矢量建立聯系。

即電流空間矢量的理解需要依托于磁動勢空間矢量，兩者之間只差一個系數，方向相同。

你將磁動勢作為空間矢量，為啥不能將電流看作空間矢量呢？

1.3 電壓空間矢量

如果說電流空間矢量尚有跡可循，那么電壓空間矢量真的似無源之水！

其實，仍舊規定，各相 電壓空間矢量方向與繞組軸線方向平行 。

還記得大明湖畔的夏雨荷嗎? 啊不，還記得理想磁鏈圓不？

既然是磁鏈圓，說明磁場方向會發生變化。什么導致磁鏈改變方向呢？因為電壓的作用啊。

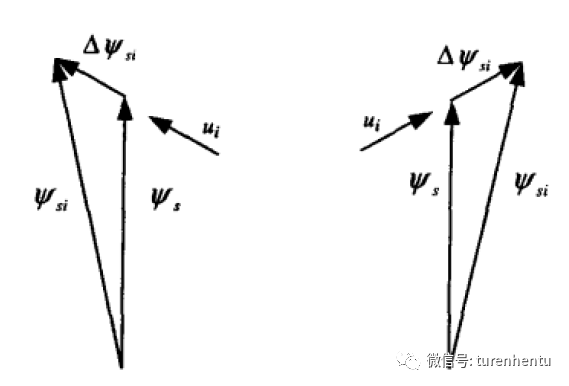
Fig 6 電壓積分改變磁鏈方向

對于定子繞組來說，滿足：

即，電壓積分導致磁鏈變化。

如下圖，合成電壓空間矢量超前合成磁動勢空間矢量90度，拉著磁鏈沿磁鏈圓運動。那么控制產生理想磁鏈圓的關鍵就是選擇合適的電壓空間矢量了。

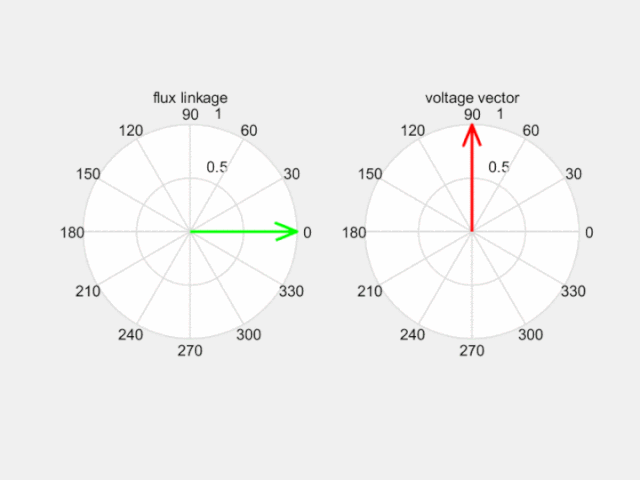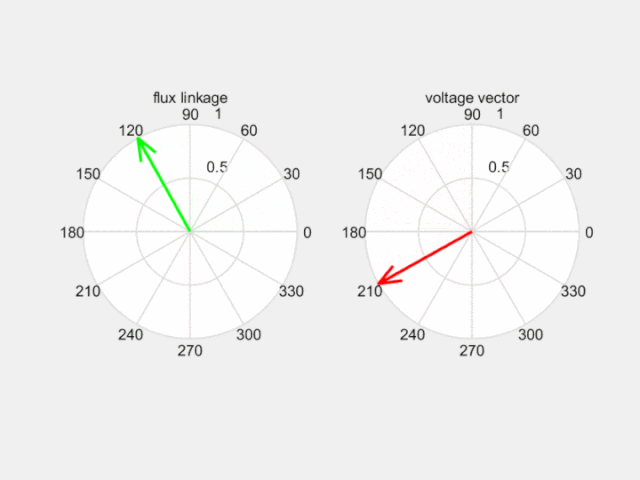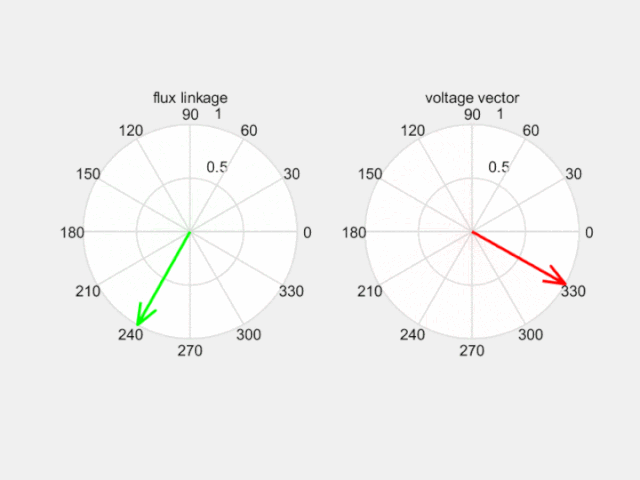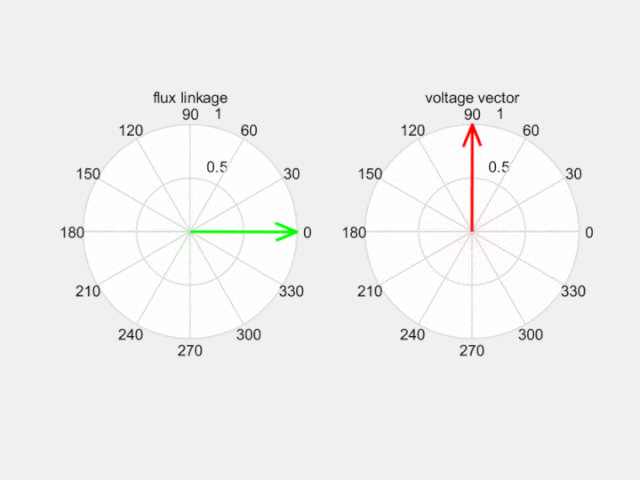
Fig 7 電壓空間矢量改變磁鏈空間矢量

那么好了，前面定義說，三相電流空間矢量/三相磁動勢空間矢量/三相電壓空間矢量均位于繞組軸線方向(或者相反方向)，你上面又說合成電壓空間矢量相位超前磁鏈90度（理想情況下）。這該如何理解呢？

由于電壓和電流本身存在時間上的相位差（理想情況，忽略電阻，電壓相位超前電流相位90度，而電流和磁動勢同相位），導致合成電壓空間矢量與合成磁動勢空間矢量在空間上存在相位差。

如下動圖：

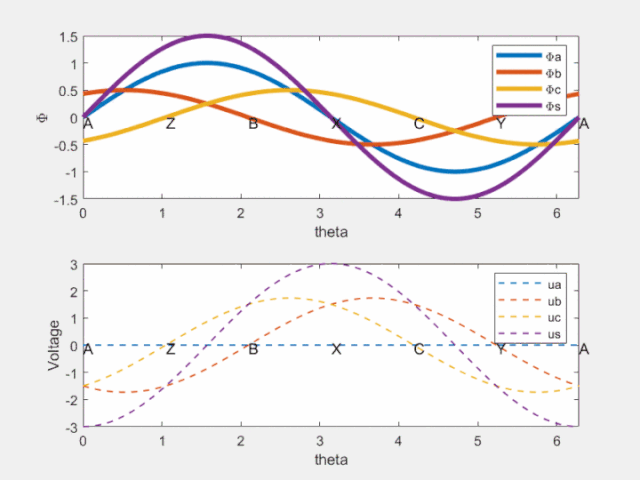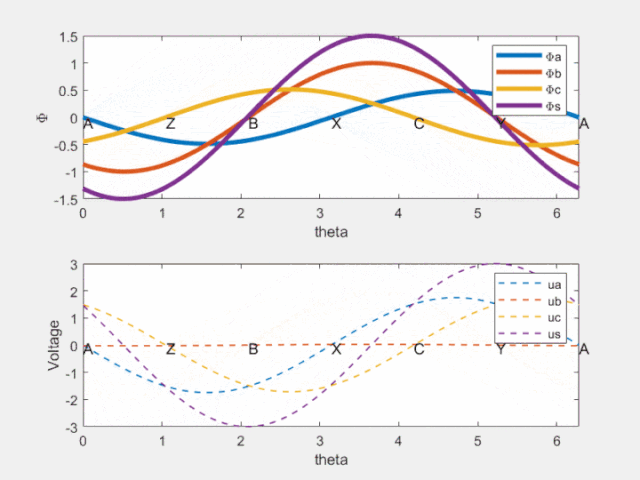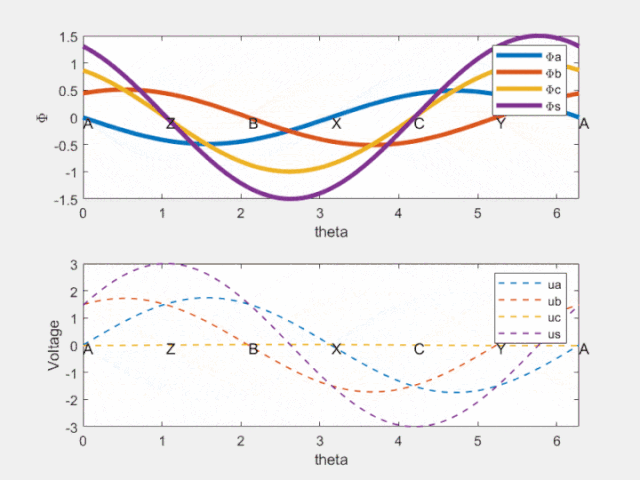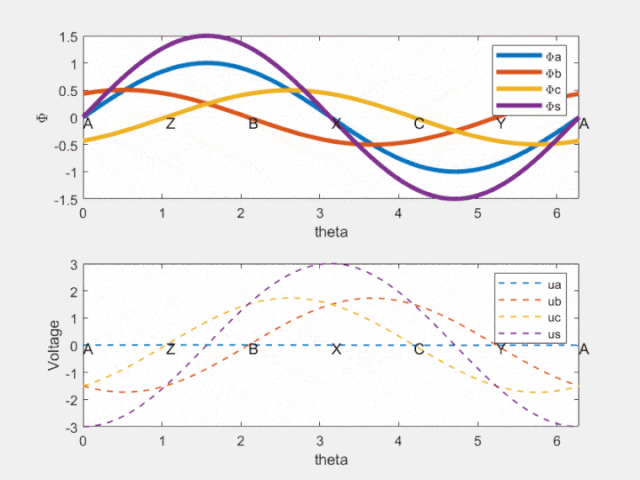
Fig 8 時間相位差反映在空間相位差

由上圖可知，紫色的虛線相位超前紫色的實線！這就是電機旋轉的原因啊

電壓空間矢量存在的前提是，仍舊需要將其和磁動勢空間矢量概念聯系起來。

推理過程見下圖：

Fig 9 空間矢量電壓公式推導

于是，你發現Uout的幅值是Ua/Ub/Uc三相電壓幅值的1.5倍。

那么空間矢量Uout在a/b/c 三軸線上的投影為多少呢？

你會發現：

而三相相電壓合成矢量如何表示呢？

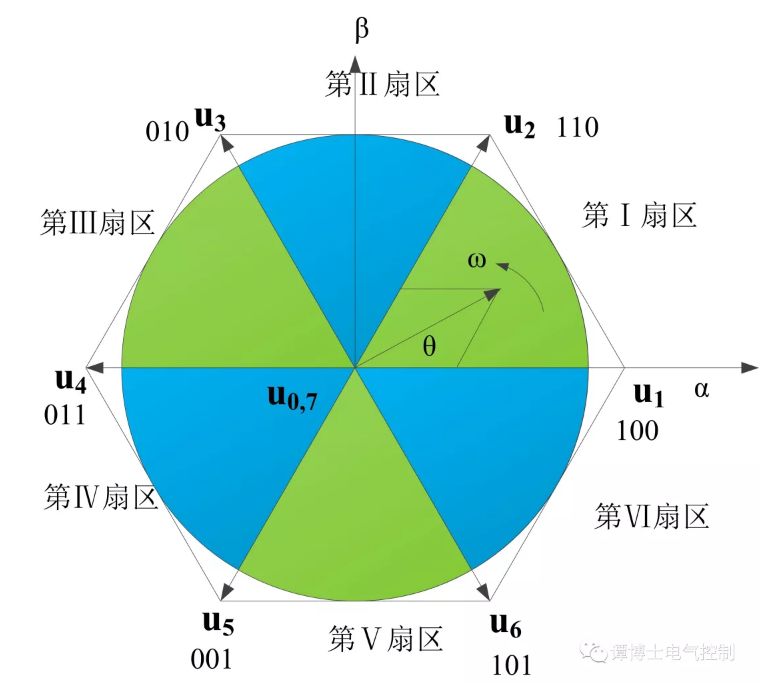
如下圖，三相相電壓合成電壓矢量的所有情況均被限制在正六邊形內部，即從正六邊形中心O點出發，終點落在正六邊形邊界上的一系列矢量（圖中只畫出了第一個扇區的部分矢量）。

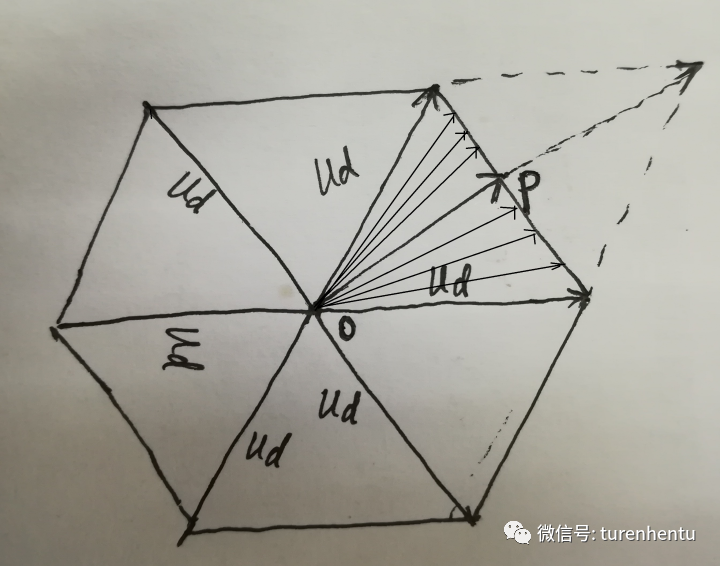
Fig 11 合成空間矢量

為什么最大的矢量是Udc呢？

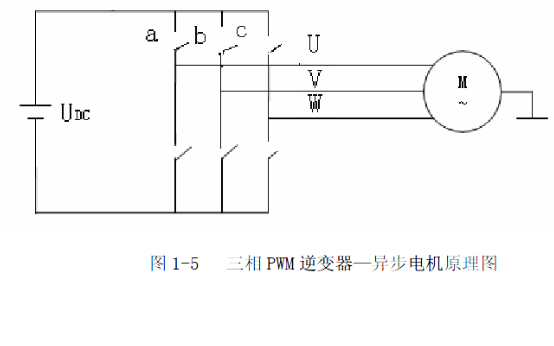
我們知道，6個功率開關可以由8個最基本的電壓矢量組合，其中6個非零的電壓矢量組合即對應圖中的6個Udc。

以a相上管導通，b，c相下管導通為例，如下圖:

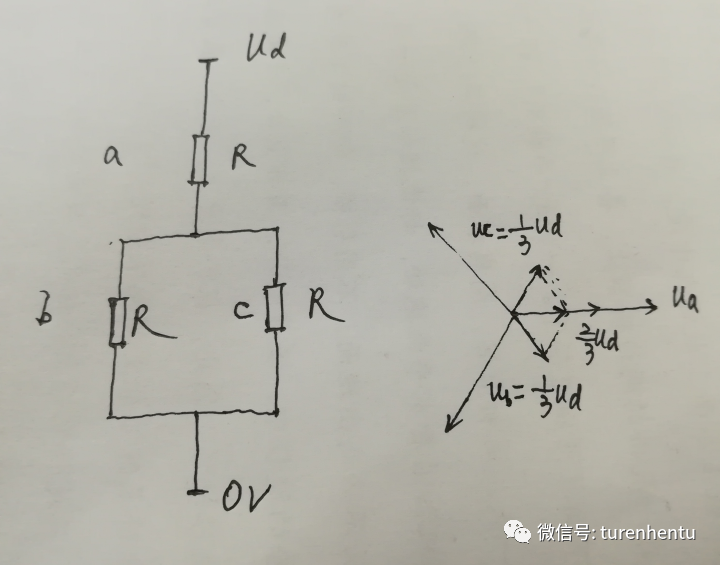
Fig 12 電壓合成矢量

此時合成的空間矢量大小為Ud。最大也只能這么大了。不信你可以試試看～

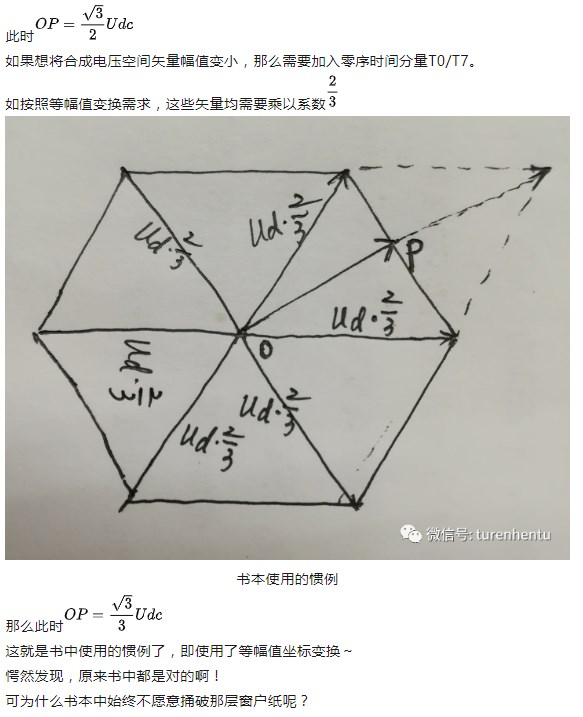
那么在P點處，三相合成電壓矢量大小還能到Ud嗎？

當然不能，前面已經說了不能超過正六邊形邊界，不管你用什么過調制方法啊，合成矢量均位于正六邊形內部。(注意，這里說的三相合成電壓矢量利用了等效的概念，即伏秒原理，如果不這樣想，那么某個瞬間，電壓矢量只能是8個基本矢量的一種情況了)。

此時應該由相鄰的兩個電壓矢量(比如U1和U2)進行等效合成。假設U1作用時間為T1，U2作用時間為T2，那么P點處，必定滿足T1+T2=Ts（Ts為時間步長），當P位于邊長中點處時，T1=T2=0.5*Ts，不要問我怎么證明了哈，我已經在圖中畫出來了。