要想知道為什么有些濾波器聽感悅耳，另一些聽起來卻并不盡如人意，你就需要深入了解濾波器的工作原理。很不幸，濾波器是所有合成器中最常被誤解的模塊。常見的誤區(qū)是：濾波器的作用就只是將信號(hào)的一部分削弱。實(shí)際上，無論是模擬還是數(shù)字世界，濾波器的功能可遠(yuǎn)遠(yuǎn)不止減弱信號(hào)這么簡(jiǎn)單。

為了能夠明確看到音頻信號(hào)在被濾波器處理的過程中到底放生了什么，你需要先理解一些相位關(guān)系的基礎(chǔ)知識(shí)。讓我們?cè)偻乜矗瑥谋鞠盗械谝黄恼轮幸氲恼也ㄩ_始說起。

首先，想象如果你使用混音器將兩個(gè)正弦波混合起來會(huì)發(fā)生什么。你可能已經(jīng)猜到了：兩個(gè)一致的波形相加得到的還是相同的波形，不過響度會(huì)更高（如圖 1）。

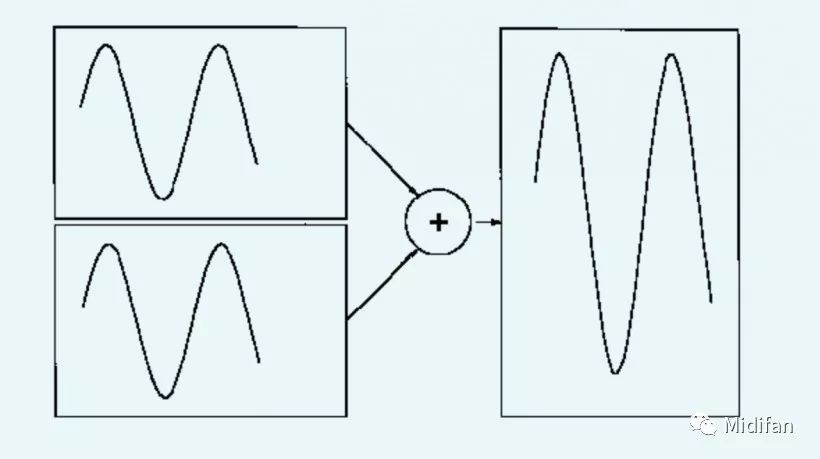
圖 1：相位一致的兩個(gè)正弦波相加之后得到響度更高的正弦波

但如果你等到上面的波形進(jìn)行到其周期一半的時(shí)候再引入下面的波形呢？圖 2 中展示了這一情況，如果你講這樣的兩個(gè)波形相加，它們會(huì)彼此抵消，因此你將聽不到任何聲音。也就是說，盡管這兩個(gè)波形單獨(dú)聽是完全一致的，但將其混合卻得到的是無聲。

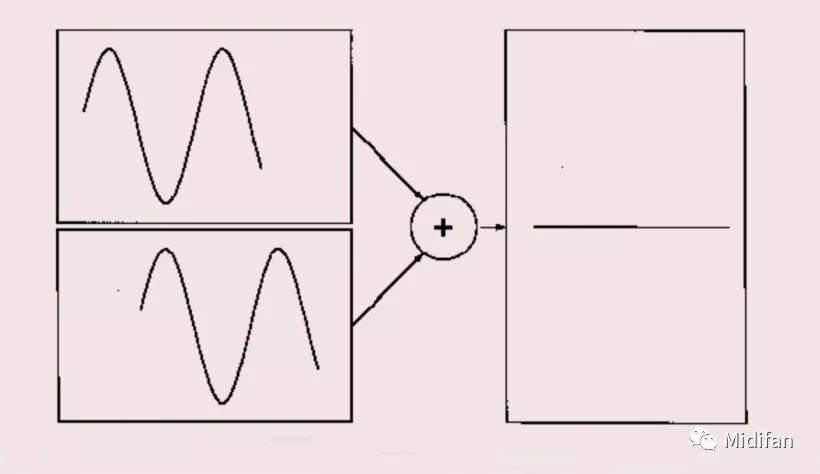
圖 2：偏移了 1/2 周期的兩個(gè)正弦波疊加之后彼此抵消

這一結(jié)果十分重要，通過該規(guī)律我們可以知道，只需要頻率與響度兩個(gè)參數(shù)就可以定義一個(gè)單一的正弦波，但如果要將兩個(gè)正弦波混合在一起，你還需要考慮兩個(gè)波形之間的偏移有多少。這樣的偏移通常被稱為一個(gè)波形與另一波形之間的「相位（phase）」。相位以度數(shù)來計(jì)量，和量角器上的度數(shù)一樣（如果你想知道為什么要用度數(shù)來表示相位的話，你可以閱讀本文末尾的「相位的度數(shù)表示」拓展部分，但如果你不想再考慮枯燥的數(shù)學(xué)知識(shí)了，可以直接繼續(xù)閱讀下面的文章）。

當(dāng)然，你可以將兩個(gè)偏移量（即相位差）任意的任何兩個(gè)正弦波混合在一起，混合后的波形的響度會(huì)處于圖 1 中的兩倍響度以及圖 2 中的 0 響度之間（但如果你將兩路信號(hào)通過立體聲而不是單聲道的方式混合，你將得到一個(gè)十分不同的效果。但這是改天的話題了，這篇文章中暫時(shí)不予討論）。

讓我們以時(shí)間差的角度來看待相位差。假如說你有一個(gè) 100Hz 的正弦波，也就是說每秒鐘震蕩 100 個(gè)周期，因此，每完成一個(gè)周期所需的時(shí)間為 0.01 秒。對(duì)于該信號(hào)來說，半個(gè)周期的偏移（如果你已經(jīng)閱讀了文末的拓展知識(shí)，你會(huì)知道半個(gè)周期的偏移等于 180 度的相位差，但如果你還沒讀，也不用擔(dān)心）為 0.005 秒，即 5 毫秒。圖 3 可以幫助你理解這一過程。

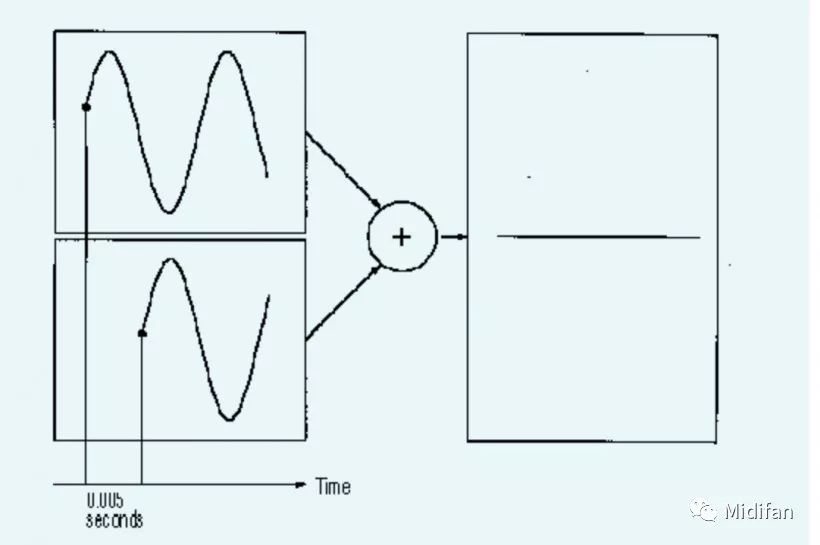
圖 3：彼此偏移半個(gè)周期（5 毫秒）的兩個(gè)正弦波相加之后相互抵消

現(xiàn)在想象兩個(gè)頻率為 200Hz 的正弦波，對(duì)于 200Hz 的波形來說，5 毫秒的時(shí)間可以完成一整個(gè)周期。如圖 4，如果使其中一個(gè)正弦波偏移 5 毫秒，另一個(gè)正弦波已經(jīng)完成了一整個(gè)周期，這時(shí)這兩個(gè)正弦波又回到了同相的狀態(tài)，如果將這樣的兩個(gè)正弦波相加，得到的會(huì)是一個(gè)響度為原波形兩倍的正弦波。

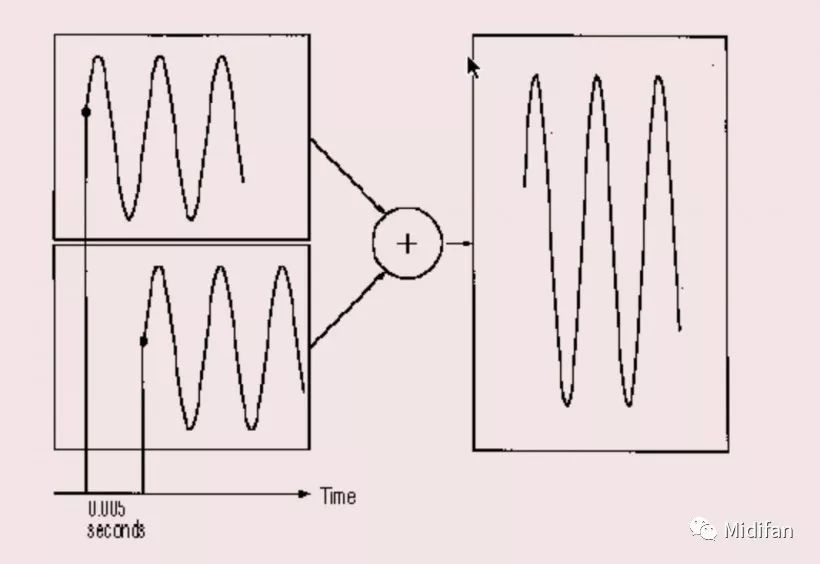
圖 4：同樣偏移 5 毫秒的兩個(gè) 200 Hz 正弦波相加之后響度翻倍

讓我們深吸一口氣，然后想想看如果把這一概念應(yīng)用于更為復(fù)雜的波形中會(huì)發(fā)生什么。以鋸齒波為例，你可能還記得我們?cè)诒鞠盗械牡谝黄恼轮薪榻B了鋸齒波的每一個(gè)諧波均存在，所以如果一個(gè)鋸齒波的基頻（即第一諧波）為 100Hz，那么其第二諧波的頻率就為 200Hz，第三諧波為 300Hz...以此類推。如果將同樣頻率，但彼此偏移半個(gè)周期的兩個(gè)鋸齒波相加，基頻會(huì)被抵消；但位于 200Hz 的第二諧波的響度會(huì)翻倍；三倍基頻的第三諧波會(huì)被抵消，但第四諧波響度翻倍，第五諧波被抵消...以此類推。這樣我們得到的將是一個(gè)諧波位于 200Hz、400Hz、600Hz...等等的波形。實(shí)際上，這一波形就是一個(gè)響度與原始波形一致，但頻率為原始波形兩倍的鋸齒波。

這一有悖直覺的結(jié)果就是我們今天的第一條結(jié)論：

將「失相」的信號(hào)混合在一起并不一定會(huì)將其兩者抵消。事實(shí)上在真實(shí)世界里完全抵消的情況幾乎根本不會(huì)發(fā)生。

但這還只是相位偏移的幾種最簡(jiǎn)單的情況之一。想想看如果將這一規(guī)律運(yùn)用于真實(shí)世界中的復(fù)雜波形上會(huì)發(fā)生什么：部分諧波的幅度會(huì)減小，另一部分諧波的幅度會(huì)增加，還有一些部分的諧波會(huì)被完全抵消，剩下一部分的諧波會(huì)完全重疊從而幅度翻倍。傅里葉分析告訴我們?nèi)魏螐?fù)雜波形——無論是人的說話聲還是樂器的聲音都可以被看作是由無數(shù)個(gè)正弦波組成的頻譜構(gòu)成的。所以說，假設(shè)對(duì)于只有相位有一定偏移，其他方面完全相同的兩個(gè)波形來說，構(gòu)成這兩個(gè)波形的每個(gè)諧波之間也會(huì)有不同幅度的相位偏移。如果在頻譜分析儀上觀察這一結(jié)果的話，你會(huì)看到一個(gè)類似于橫放的梳子的圖案，「梳齒」之間的距離（即被抵消的諧波）由時(shí)間差決定（見圖 5）。

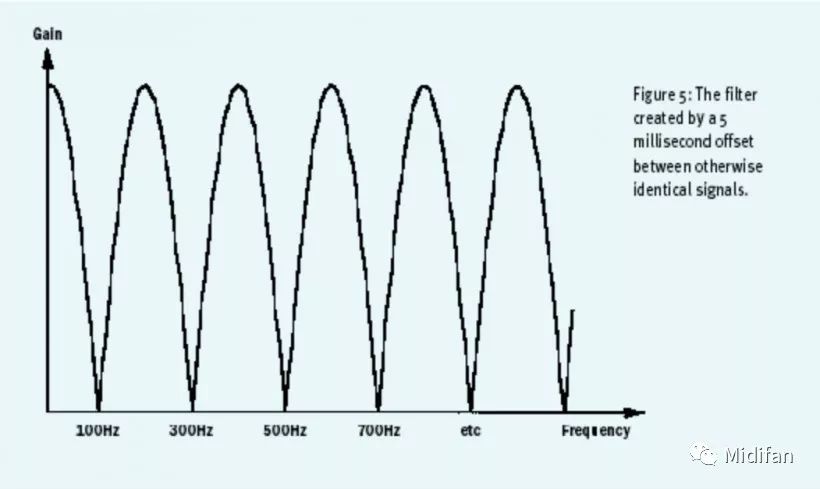
圖 5：相互偏移 5 毫秒，但其他方面完全相同的兩個(gè)波形疊加產(chǎn)生的濾波

換句話說，當(dāng)你將除了相位偏移之外其他方面完全相同的兩個(gè)波形混合在一起時(shí)，兩個(gè)波形的諧波之間的相位差導(dǎo)致了濾波。因?yàn)檫@種濾波的形狀與梳子十分形似，所以使用這一技術(shù)的濾波器被稱為梳狀濾波器（Comb Filter）。梳狀濾波器在合成器中被廣泛運(yùn)用，從經(jīng)典的模擬模塊化合成器 Analogue Systems RS Integrator 到基于 DSP 的 Waldorf Q 上都可以找得到到梳狀合成器的身影。

了解了關(guān)于相位的的知識(shí)之后，不難看到相位與音頻濾波之間的密切關(guān)聯(lián)。但想想看，如果相位變化可以導(dǎo)致濾波，那么濾波能否導(dǎo)致相位變化呢？答案是：當(dāng)然可以。

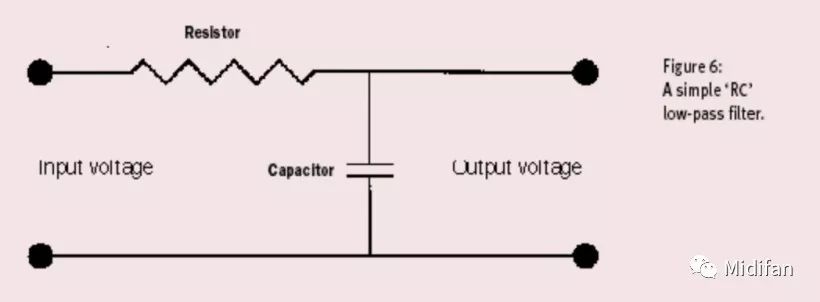
圖 6：一個(gè)簡(jiǎn)單的 RC 低通濾波器電路

觀察圖 6 中的電路圖，這一電路非常簡(jiǎn)單，只使用了兩個(gè)電子元器件：一個(gè)電阻器與一個(gè)電容器，不過這一簡(jiǎn)單電路構(gòu)成一個(gè)完全可用的濾波器，叫做 RC 低通濾波器。任何新手合成器用戶都知道，低通濾波器允許低于「截止頻率」的所有諧波通過，所有高于截止頻率的諧波則會(huì)被削減。對(duì)于這一簡(jiǎn)單的濾波器來說，它的截止頻率取決于其元器件的參數(shù)，截止頻率以上的信號(hào)被削減的速率則由電路的構(gòu)造決定。

我們暫時(shí)不考慮信號(hào)被削減的速率，這一話題將留給下一篇文章探討。本文我們將專注于這一濾波器會(huì)對(duì)被輸入進(jìn)去的信號(hào)相位造成什么樣的影響。

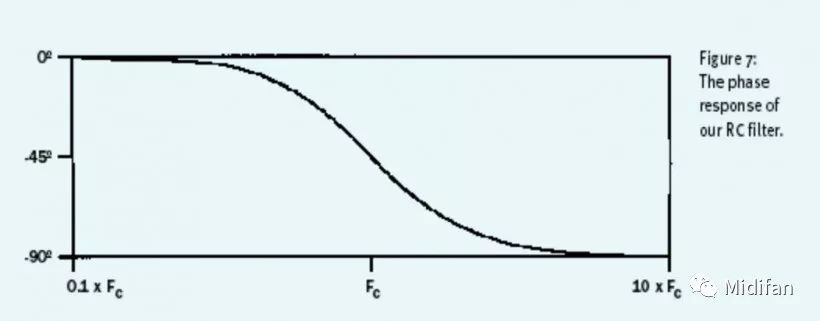
圖 7：上文 RC 濾波器的相位響應(yīng)

觀察圖 7，該圖是上文的簡(jiǎn)單 LPF 的「相位響應(yīng)（phase response）」屬性。該圖展示了任意被輸入進(jìn)濾波器中的頻率及其相位將被偏移的程度。不難看到，該濾波器幾乎沒有對(duì)低頻信號(hào)的相位產(chǎn)生大幅影響，然而信號(hào)頻率越高的位置，其相位被偏移得就越大。位于截止頻率的信號(hào)被偏移了八分之一周期（-45 度），信號(hào)最高頻的位置則被整整偏移了 -90 度。

由于這些概念有些難懂，讓我們以 100Hz 的方波為例，看看這一 RC 濾波器在實(shí)際的模擬合成器中到底起什么樣的作用。

正如我們?cè)诒鞠盗械牡谝黄恼轮薪榻B的：任何傳統(tǒng)波形都可以被分解成一些列諧波，這些諧波被稱為基礎(chǔ)頻率及其泛音。這一例子中，我們的輸入信號(hào)（方波）的基礎(chǔ)頻率為 100Hz，其第二諧波（200Hz）不存在，但擁有位于 300Hz 的第三諧波，并且第三諧波的幅度為基頻幅度的三分之一。接著，第四諧波不存在，幅度五分之一的第五諧波位于 500Hz 的位置，以此類推...當(dāng)其所有諧波均同相的情況下，該波形如圖 8 所示。

圖 8：理想狀態(tài)下的 100Hz 方波

現(xiàn)在，假設(shè)我們的簡(jiǎn)易 RC 濾波器擁有 400Hz 的截止頻率，并且該濾波器截止頻率一下的相位響應(yīng)均為 0。這種情況下的結(jié)果應(yīng)該不難想象：波形的基頻與第一泛音（100Hz 與 300Hz）將不會(huì)被減弱，但所有高于 500 Hz 的泛音均會(huì)根據(jù)相位響應(yīng)發(fā)生相應(yīng)幅度的衰減。經(jīng)過這一處理之后的波形（可能會(huì)和你的預(yù)料有些不同）如圖 9 所示。

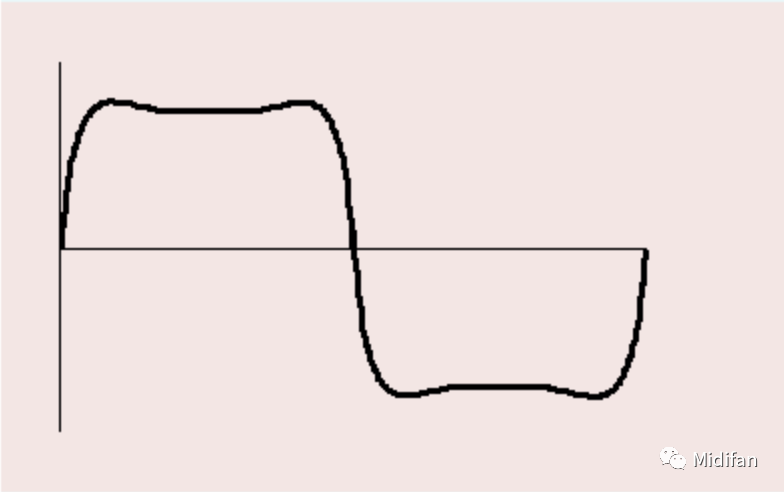
圖 9：理想狀態(tài)下經(jīng)截止頻率為 400Hz 的 RC 濾波器處理的 100Hz 方波

現(xiàn)在再讓我們把濾波過程中每個(gè)諧波產(chǎn)生的相位偏移考慮進(jìn)來，我們現(xiàn)在得到的將會(huì)是一個(gè)形狀十分不同的波形。可以看到，經(jīng)過濾波之后的真實(shí)波形與原始方波比起來產(chǎn)生了明顯的失真（如圖 10）。

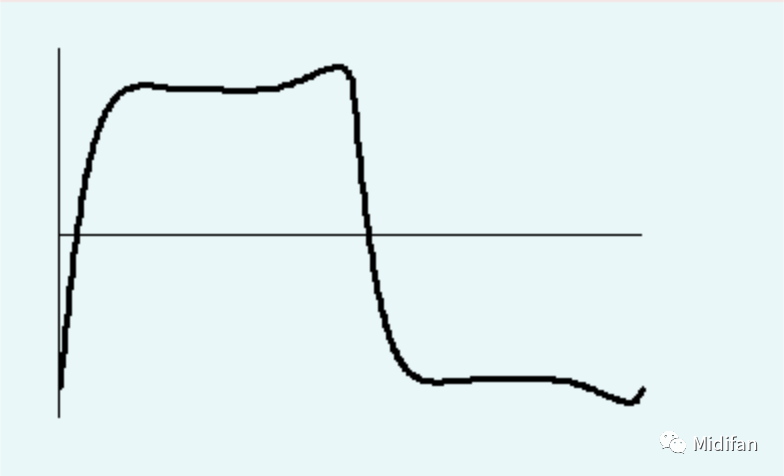
圖 10：濾波產(chǎn)生的實(shí)際波形

由此我們可以得到本文最重要的規(guī)律：

濾波器不光只是使波形的諧波產(chǎn)生衰減，它還可以通過改變諧波的相位偏移從而使得波形失真變形。

不過由于本文列舉的方波與濾波器非常簡(jiǎn)單，盡管可以看到經(jīng)過濾波的圖 9 與圖 10 中的波形與原始波形的區(qū)別，你可能并不能聽出濾波造成明顯的差異。但還是那句話，真實(shí)世界中的聲音要比簡(jiǎn)單的方波等波形復(fù)雜得多，濾波可以對(duì)許多真實(shí)聲音造成巨大的改變。當(dāng)然，濾波器的種類也遠(yuǎn)不是只有本文中列舉的簡(jiǎn)易 RC 低通濾波器一種，如果使用的是 Moog 濾波器的話，濾波產(chǎn)生的效果又會(huì)與上文大相徑庭...不過我們暫時(shí)先把這些留給以后的文章。

拓展知識(shí)：為什么相位偏移可以用度數(shù)表示

數(shù)學(xué)中的度數(shù)不是用來描述角度的大小與旋轉(zhuǎn)的幅度的嗎？這要取決于你如何看待這一問題。想象一個(gè)正弦波波形，如下圖中的 (c)。在某一時(shí)刻，該波形從零點(diǎn)開始上升，運(yùn)動(dòng)到其周期 1/4 的時(shí)刻到達(dá)頂峰，到周期一般的位置重歸零點(diǎn)，運(yùn)動(dòng)至 3/4 周期的時(shí)候跌至最低，然后在周期最末尾重歸零點(diǎn)，往復(fù)循環(huán)進(jìn)行。

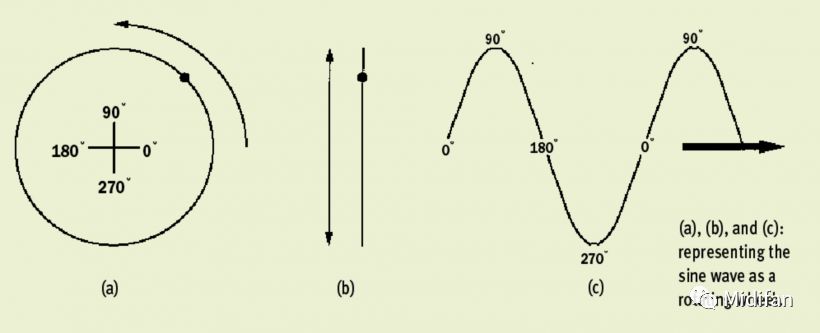
然而正弦波的波形可以用另一種方式描述。想象一個(gè)圓盤以一個(gè)固定的速度旋轉(zhuǎn)，如上圖中的 (a)，如果只考慮圓周上的任意一個(gè)點(diǎn)的縱向運(yùn)動(dòng)軌跡，你得到的將是上圖中 (b) 這樣的上下往返移動(dòng)。但想象將這一上下移動(dòng)軌跡畫在一張紙上，但在同時(shí)以固定的速度橫向移動(dòng)這張紙，你得到的也將會(huì)是上圖中 (c) 的正弦波，如下圖所示：

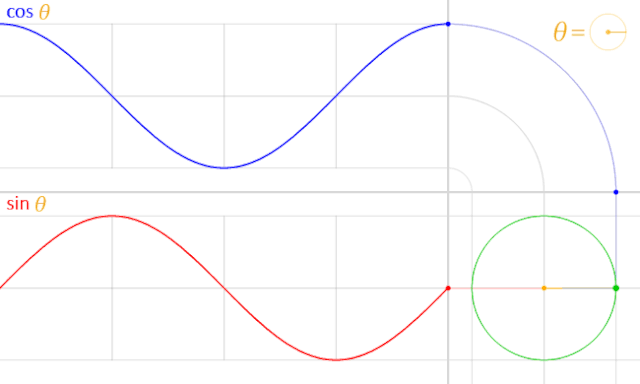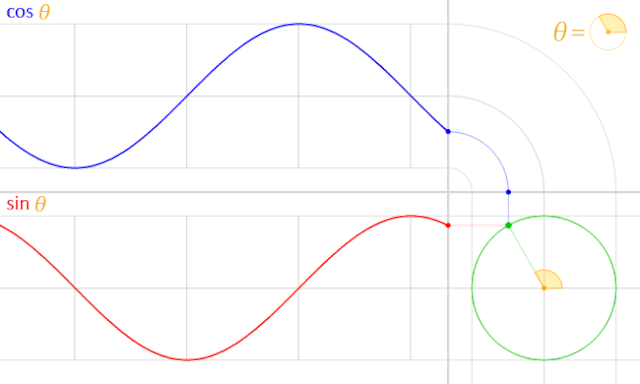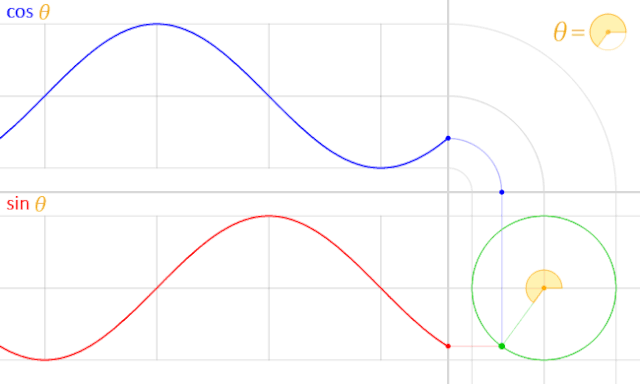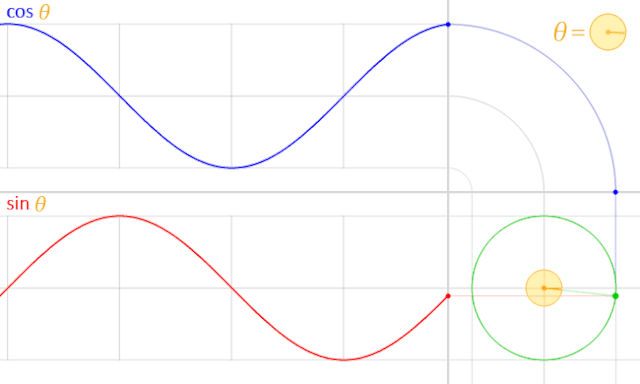
通過這一思路我們可以使用度數(shù)這一個(gè)單位同時(shí)表示圓周旋轉(zhuǎn)的幅度與正弦波的周期。正弦波由 0 度開始，到達(dá)最高點(diǎn)時(shí)位于 90 度，進(jìn)行至 180 度時(shí)降回 0，到達(dá)最低點(diǎn)時(shí)位于 270 度，與 360 度的時(shí)候完成一整個(gè)周期，與 0 度重疊。

這是一種表示波形屬性的巧妙方式，并且可以非常簡(jiǎn)單地描述相對(duì)相位。比如說，如果兩個(gè)正弦波彼此相位偏移半個(gè)周期，那么你就可以說這兩個(gè)波形處于「180 度失相關(guān)系（因?yàn)楫?dāng)一個(gè)波形位于 180 度的時(shí)候另一個(gè)波形位于 0 度的位置）」。