我們有提到調制信號源不光只可以是低頻振蕩器或者包絡生成器的信號。當然，我們對聲音進行調制時大多數情況下使用上面的低頻信號，并且大多數非模塊化合成器只允許我們使用上述低頻信號對音色進行調制。不過幸運的是，部分強大的合成器允許我們使用人類聽覺范圍內的高頻信號或音頻信號對振蕩器、濾波器或 VCA 進行調制。運用這類調制我們可以制作出許多使用其他手法難以得到的音色。

如果調制的信號源是一個音頻頻率范圍的振蕩器，而且調制對象為音頻信號流中的 VCA 增益，那么我們管這樣的調制叫做振幅調制（Amplitude Modulation），或者簡寫成 AM。振幅調制在我看來是一個非常有趣的話題，其中的一個原因是 AM 可以造成十分出人意料的效果：AM 造成的并不是極其迅速的顫音，而是原始信號中并不存在的諧波頻率！但這一現象是怎樣產生的呢？

振幅調制的原理其實十分反直覺，所以我們要使用數學才能對它進行理解。盡管 AM 背后的數學原理并非極其復雜，但如果你想跳過本文的下一部分直接閱讀本文后半的實際運用也完全沒有問題。如果你想嘗試理解 AM 的數學原理，不妨繼續閱讀，或許你也會覺得它其實蠻有意思…

A?=a?cos(w?t)

算式 1: 一個簡單的余弦波

利用算式 1 我們可以求得一個余弦波頻率（w）在任意瞬時（t）的振幅（即任意時刻時波形的幅度，A）。當然，我們完全可以使用正弦波取代這里的余弦波，畢竟兩者的波形完全一致，它們唯一的區別在于相位，但這里我之所以使用余弦波是因為這樣可以些許簡化我們需要的數學運算。上述算式中還有另外一個變量，小寫 a 用來代表波形振幅的峰值（波形一個周期內幅度的最大值）。

你或許注意到了算式 1 中的每個變量（時間 t 除外）的右下方都有一個「1」的角標，這一角標是用來將下文中的算式與我們的第一個波形區別開來的。

A?=a?cos(w?t)

算式 2: 另外一個余弦波

觀察算式 2，不難發現算式 2 和算式 1 完全一致，唯一的區別在于變量的角標為 2，而不是 1。這說明我們有另外一個波形需要考慮，并且這一波型擁有與算式 1 不同的最高振幅以及振蕩頻率。

讓我們假設信號 1 的振幅 a? 為信號 2 振幅 a? 的二分之一。讓我們將兩個信號的振幅分別叫做增益 1 和增益 2。現在讓我們假設波型 1 的頻率 w? 是波型 2 頻率 w? 的 1.5 倍，比方說信號 1 的頻率為 300Hz，信號 2 的頻率為 200Hz。這兩個信號的波形分別為圖 1 和圖 3，它們的頻譜構成分別為圖 2 和圖 4。雖然上面的兩個算式看上去或許晦澀難懂，但大多數人對于圖 1 和圖 3 的波形都多多少少有所熟悉，其實上面的算式和波形圖表示的是完全一致的信息。

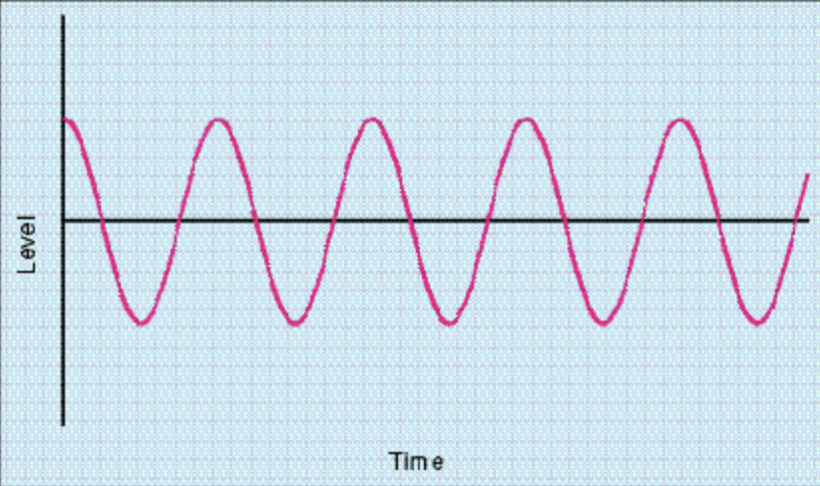
圖 1: 信號 1: a? = 1, w? = 300Hz

圖 2: 信號 1 的諧波成分

圖 3: 信號 2: a? = 2, w? = 200Hz

圖 4: 信號 2 的諧波成分

現在讓我們想象一下如果將上面的兩個信號混合起來會發生什么。圖 5 展示的是混合音頻信號的合成器流程圖，圖 6 則是經過混合的復合信號（這一復合信號任意時刻的振幅均為兩條原始信號同樣時刻的兩波形振幅之和），圖 7 是這一信號的諧波構成。

圖 5: 將兩條音頻信號混合

圖 6: 將圖 1 與圖 3 中的波形混合得到的復合波形

圖 7: 上述復合波形的諧波分布

這一結果并非十分有趣。但讓我們對上面的合成器流程進行些許改變，將信號鏈中的混音器用壓控放大器，即 VCA 代替。接著讓我們把信號 1 輸送至 VCA 的音頻輸入中，不過這次讓我們使用信號 2 調制該 VCA 的增益參數，就像我們在上一篇文章中使用 LFO 一樣。因此，信號 2 成為這一流程中的調制器（Modulator），而信號 1 則為載波器（Carrier），見圖 8。

圖 8: 使用音頻范圍的信號進行振幅調制

別忘了，算式 1 中變量 a? 代表的是波形的最大振幅，為了便于理解，讓我們假設這一振幅等于 VCA 的增益。但因為我們現在使用第二條信號的瞬時振幅來對原始信號進行調制，所以當調制器信號的波形為正值（即其電壓高于 0V 軸）時，VCA 的增益將隨之上升，當調制器波形為負值時，VCA 的增益將隨之減弱。但調制器信號在任意時刻的振幅 A? 我們都可以使用算式 2 進行計算。

所以我們現在可以得到一條新的算式，該算式輸出信號的振幅為 a? 與 A? 只和：

A?=(a? + A?)cos(w?t)

算式 3: 決定輸出信號波形的算式

我們可以將算式 2 中 A? 的求法代入至算式 3，從而得到算式 4，然后將其展開得到算式 5：

A?=(a? + a?cos(w?t))cos(w?t)

算式 4: 將 A? 代入至算式 3

A?=a?cos(w?t) + a?cos(w?t)cos(w?t)

算式 5: 將算式 4 展開的結果

算式 5 看上去或許要比算式 3 復雜，但兩者描述的信號與 VCA 關系其實完全一致。觀察算式 5 的右半邊，你會發現它包含兩個余弦函數的乘積。余弦函數的乘積很難進行直觀理解，不過幸運的是利用一條數學原理，我們可以將頻率為 X 和 Y 的兩條余弦函數的乘積分離成 cos(X+Y) 和 cos(X-Y) 兩項。如果你不理解上面這一部分，別擔心，你只需要記住我們可以將算式 5 中的右邊一項分離成算式 6 中的兩項，其中一項是頻率為 w? + w? 的波形，另一項是頻率為 w? - w? 的波形。

A?=a?cos(w?t) + 1/2(a?cos(w? + w?)t) + 1/2(a?cos(w? - w?)t)

算式 6: 振幅調制的結果

仔細觀察算式 6，你會發現該算式的第一項與算式 1 中的原始余弦波，即載波器信號完全一致。現在請思考一下算式 6 第二項中的 w? + w? 的意義。這一定代表的是頻率為載波器與調制器頻率只和的波形。同樣的，第三項代表的是頻率為載波器與調制器頻率之差的波形。換句話說，振幅調制不光保留了原始的載波器信號，還制造了分別叫做和（Sum）與差（Difference）的兩條全新信號。

圖 9: 使用信號 2 對信號 1 進行振幅調制得到的結果

圖 9 展示的是算式 6 代表的波形。可以看到這一波形要比圖 6 中簡單地將兩條信號混合起來制造的波形復雜得多。

圖 10: 圖 9 波形的諧波分布

圖 10 為圖 9 波形的頻譜，注意調制器的原始頻率完全消失，生成的和差信號分別具備調制器原始振幅的二分之一（算式 6 中的 1/2 也說明了這一點）。

介紹了這么多振幅調制的理論，讓我們討論一下怎樣可以將 AM 技術實際運用至合成器中。要想回答這一問題，我們需要考慮振幅調制的兩種情況：第一是調制器頻率保持恒定時的情況，另外一個是調制器和載波器兩者的頻率均由鍵盤（或者其他任何控制電壓）控制時的情況。

讓我們先來思考一下使用鍵盤演奏載波器信號，而調制器信號（恒定振幅）的頻率保持不變（比如說 100 Hz）時的情況。

例 1

當載波器頻率同樣為 100 Hz 時，振幅調制造成的三個頻率分別為：原始的 100Hz，100 - 100 = 0Hz，以及 100 + 100 = 200Hz。它們分別為載波器的原始信號、振幅調制的差信號以及和信號。或許你會認為頻率為 0Hz 的信號并不具備任何影響，然而事實并非如此。這一頻率仍然具備（調制器信號二分之一的）振幅，因此可以導致輸出信號的偏移。我們將這一現象稱作 DC 偏移（direct current offset，直流偏移），因為位于 0Hz 的信號不具備振蕩頻率。觀察圖 11，可以看到輸出信號的一大部分位于 0V 線之上，這一現象就是 DC 偏移導致的。當信號被合成器的其他模組，例如濾波器和放大器進行處理時， DC 偏移可能會造成明顯的影響。但本文我們并不會對此進行深入探討。

圖 11: 載波器振幅 a? = 1，頻率 w? = 100Hz，調制器振幅 a? = 1，頻率 w? = 100Hz 的振幅調制

振幅調制后的另外兩條信號分別為位于 100Hz 的載波器原始信號和位于 200Hz 的和信號。當然，這里的和信號頻率正好是載波器原始頻率的兩倍，也就是說它比載波頻率正好高一個八度，因此這一結果聽上去會十分諧和，或者「悅耳」。我們可以將輸出的三條頻率分別概括為載波器頻率的百分之 0、百分之 100 和百分之 200。

例 2

假設我們將音符從鍵盤上移高一點，比如說現在的載波器頻率為 200Hz。因為調制器的頻率保持 100Hz 不變，所以振幅調制造成的三個頻率分別為載波器原始的 200Hz、載波與調制信號的頻率差 100Hz 以及頻率和 300Hz。該振幅調制的結果多多少少仍然諧和，因為差信號正好位于載波器信號的一個八度之下。然而和信號與載波器并不具備諧和關系。盡管如此，這一情況也還是一個特例，因為和信號為差信號的第三諧波，因此最終的輸出信號仍然具備一定的「音樂性」，盡管載波器（差信號的第二諧波）是主導頻率。我們可以將該情況的三條頻率概括為載波器頻率的百分之 50、百分之 100 和百分之 150。

例 3

現在讓我們為載波器選擇一個較為隨機的頻率。比如說如果我們的載波器頻率為 371Hz 時將會得到什么樣的結果呢？這時的和差信號分別為 271Hz 和 471Hz，它們之間不存在諧和關系。輸出波形的三個頻率分別大致位于載波信號的百分之 73、百分之 100 和百分之 127 的位置。因此我們將最終得到一個不和諧的聲音。

實際上，當調制頻率保持不變時，振幅調制制作的大多數音色都將會是類似上面的不諧和聲音。類似例 1 和例 2 的特例其實十分罕見。因此固定調制器的 AM 合成最適合用來制作演奏不同琴鍵時變化巨大的激進、非常規的音效。你可以通過提升或降低調制器的振幅從而控制音色不諧和的程度。

例 4

讓我們回到例 2，載波器仍具備 200Hz 的頻率，調制器頻率為 100Hz。和之前一樣，輸出信號仍將包含原始的 200Hz，以及和差信號的 300Hz 和 100Hz。不過這次我們會對合成器的流程進行些許改變，使得當你使用鍵盤演奏載波器時，調制器的頻率也會隨之改變。比如說，如果你演奏一個頻率為 400Hz 的載波信號（原始 200Hz 的一個八度之上）調制器的頻率也將隨之翻倍，和差信號因此將分別變成 600Hz 和 200Hz。不管演奏什么樣的音符，差、載波與和信號的頻率將總是保持百分之 50、百分之 100 和百分之 150 的比率。盡管最終的輸出信號頻率翻倍，其波形將保持不變，因此我們可以得到一個恒定不變的音色。這類振幅調制可以幫助我們制作可以使用鍵盤正常演奏的擁有復雜諧波構成的音色。

總而言之：振幅調制可以幫助我們制作和演奏僅僅使用傳統振蕩器難以得到的復雜音色。

當然，直到這里我們所討論的還僅僅只是簡單的正弦波的振幅調制。你當然還可以使用其他類型的波形進行振幅調制。如果調制器和載波器分別具有一個基礎頻率和一個額外的諧波，那么使用振幅調制，我們得到的將不僅僅是一條差信號和一條和信號總共兩條新信號，而是八條全新的諧波。如果調制和載波頻率分別具備三條諧波，那么振幅調制將生成 18 條額外的諧波。如果它們分別具備四條諧波，生成的諧波將上升至 32 條，以此類推…

我們完全可以使用擁有復雜諧波構成的波形，比如說方波或鋸齒波等波形進行振幅調制。這些復雜波形的振幅調制和簡單的正弦波振幅調制原理完全相同，不過為了理解它們我們需要進行許多次計算。

或許你還記得鋸齒波具有基礎頻率的所有整數倍諧波。比如說，一個基礎頻率為 100Hz 的鋸齒波頻譜由 100Hz, 200Hz, 300Hz, 400Hz 等等整數倍諧波構成。75Hz 的鋸齒波頻譜中包含的頻率則為：75Hz, 150Hz, 225Hz…以此類推。所以如果用一個頻率為 75Hz 的調制器對 100Hz 的載波信號進行振幅調制將會得到怎么樣的結果呢？

不難想象載波信號的基頻將與調制器的基頻進行交互，產生頻率為 25Hz, 100Hz, 與 175Hz 的三條諧波。它同時也會和調制器的第二諧波進行相互作用，產生 -50Hz, 100Hz, 以及 250Hz 的另外三條諧波（你或許在想 -50Hz 的頻率是什么樣的，其實負數頻率和正頻率聽起來完全相同，也就是說你將簡單地聽到 50Hz 的聲音）。接著是調制器的第三諧波（造成 125Hz, 100Hz 和 325Hz諧波）、第四諧波、第五和第六等等等等…天吶，好復雜！

但這還不算完，別忘了載波器的第二諧波也會與調制器的所有諧波頻率產生交互，接著是載波器的第三諧波、第四諧波、第五諧波…等等等等。幸運的是，鋸齒波等波形除了前幾個諧波之外的其他諧波頻率振幅都十分微小，因此在實際的運用中你可以多少忽視復雜波形的高次諧波。即便如此，不難想象對這些復雜波形進行振幅調制將會得到十分復雜的音色。振幅調制得到的波形可以作為使用濾波器和其他調制器進行復雜音色合成時十分不錯的起點。

上面的所有例子中我們都假設你的合成器中的 VCA 完美運作，并且沒有任何調制信號泄漏至最終的輸出信號中。然而根據我的經驗，事實完全并非如此，不過極其高品質的 VCA 可以保證信號泄漏處于合理的水平。盡管如此，即使僅僅只有一小部分調制信號泄漏至輸出信號也會明顯增添最終音色的不諧和感。

不過，還有另一種合成器模塊可以（在理想情況下）將調制器和載波器的信號一同從輸出信號中除去。這類模塊叫做環形調制器（Ring Modulator，RM），雖說環形調制聽上去很神秘，其實它只是振幅調制的一種特殊情況。另外，環形調制只有在調制信號和載波信號兩者波形中心準確居于 0V 軸時才可以進行。為了實現這一點，許多環形調制器具備 AC 耦合（AC-couple）功能，也就是說（至少在理想情況下）輸入信號中的任何 DC 偏移將會在進行調制之前被除去。環形調制得到的聲音只含兩條輸入的和差信號，并不包含任何輸入信號本身。還有一小部分環形調制器具備 DC 耦合功能，它們的運作方式和 AC 耦合 RM 有些許區別。其中最明顯的區別在于它們允許將載波和調制的原始信號輸送至最終輸出的信號中。ARP 2600 等合成器中的 RM 調制器允許你在 AC 和 DC 耦合模式之間進行切換，以便制作兩類不同的聲音。

本文的最后，請思考一下如果我們使用信號 2 對低通濾波器的截止頻率，而不是 VCA 的增益進行調制時將會發生什么呢？別擔心，這一情況并不需要復雜的討論和難以理解的數學原理。

想象一個復雜波形，它的其中一個諧波剛好位于濾波器截止頻率 Fc 上方的某個位置。當你對 Fc 的頻率進行調制時，你會發現有時該諧波的振幅會隨著調制大幅度衰減，而另外一些時候衰減則并沒有這么巨大。換句話說，該諧波其實相當于在被濾波器的行為變化而振幅調制。信號中的其他諧波也會根據調制的寬度（調制器的最大振幅 a?）或多或少受到同樣的影響。所以說這時，并不是一系列諧波在被另一系列諧波調制，我們只有一系列諧波，但其中的每一個單一諧波都以不同方式在被進行調制。

終于，對于振幅調制（即音頻信號范圍內的震音）和濾波器調制（即音頻信號范圍內的嗥音）的討論到此為止就告一段落了。不過，既然我們可以用音頻范圍內的信號對 VCA 的增益和濾波器的截止頻率進行調制，我們也一定可以使用音頻信號對振蕩器的振蕩頻率進行調制吧？沒錯，我們管這類調制叫做頻率調制（Frequency Modulation，即 FM）。