1,為什么最小均方差是最優的
卡爾曼濾波本質上是尋找兩個分布線性組合取得最新小均方差的問題。然后擴展到多維向量空間。
那么思考一下問什么當兩個分布取得最小均方差的時候最優?
首先我先說明一下, 最小均方差并不是最優,而是很優。因為本質上是無法確定那種最優 。
所以為了工程上的可行我們通常是綜合兩個不同的測量數據,或者多一些也就四五個。那么這個時候求兩個數據的均值是最優的嗎?當然不是,以電子槍和水銀溫度計來說,通常水銀溫度計的測量更加準確,電子槍的測量誤很大,所以如果我們求平均值的時候電子槍測量結果對最終預測的結果影響權重太大了,顯然不合適。那么究竟怎么的比例合適?

我們要尋找最優的K,為什么可以用方差呢?方差是不是最優呢?我們說貧富差距大,實際就是因為方差很大,但是如何評價兩個國家哪個國家的貧富差距更大呢?僅僅用方差可以嗎?顯然是不行的,比如兩個國家一個是富人和窮人都很多,計算一個方差,但是另外一個國家富人只有幾個,除此之外其他的人都很平均,但是計算出來的方差更大,那么我們能認為第二個國家貧富差距更大嗎?顯然不行。 盡管沒有最理想的模型,但是方差確實是可以在一定程度上說明貧富差距,能一定程度說明圍繞期望波動的劇烈程度 。那么這樣我們當然可以將尋找方差最小作為不錯的估計結果, 所以我們也可以定義這樣的結果是按照方差大小來分布的最優 。
2,卡爾曼濾波擴展和數學本質

這個K值就和過程控制迭代中提到的卡爾曼增益成比例 ,
過程控制中的計算是卡爾曼濾波思想的應用。因為迭代以及多維空間導致很難理解 。
之所以我們看到的卡爾曼濾波很復雜是因為是用于過程控制迭代加上向量計算掩蓋了本質,導致難以理解

3,卡爾曼濾波和互補濾波
還是以測溫為例子,假設水銀溫度計的精度高,測溫槍的精度低。在一個測量過程中,我如果是卡爾曼濾波我們要不斷的計算卡爾曼增益,顯然這個效率精度更好,但是許多時候計算量大一點。如果我們并不要求特別高的精度,我們就可以用下面的互補濾波來預測。互補濾波本質上就是固定卡爾曼濾波系數的簡化版本,每一次迭代的卡爾曼濾波系數都不變。

許多精度要求不高環境比較穩定的情況下,互補濾波就可以滿足使用
-
濾波器
+關注
關注
161文章
7843瀏覽量
178378 -
卡爾曼濾波
+關注
關注
3文章
166瀏覽量
24659
發布評論請先 登錄
相關推薦
卡爾曼濾波的變種有哪些?1
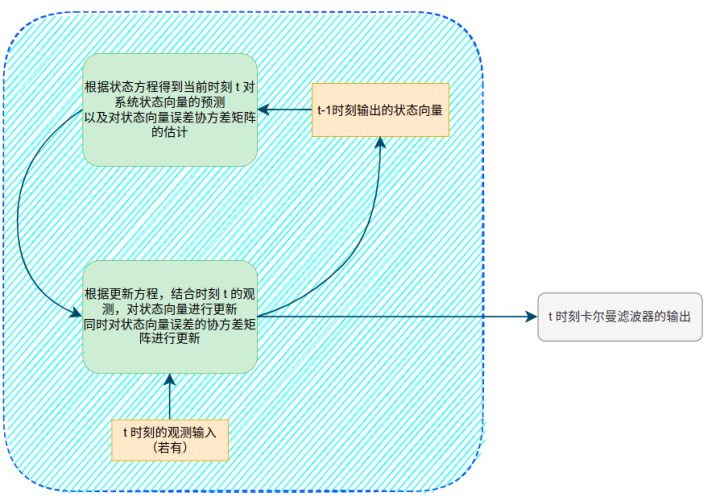
卡爾曼濾波的變種有哪些?2
卡爾曼濾波的變種有哪些?3
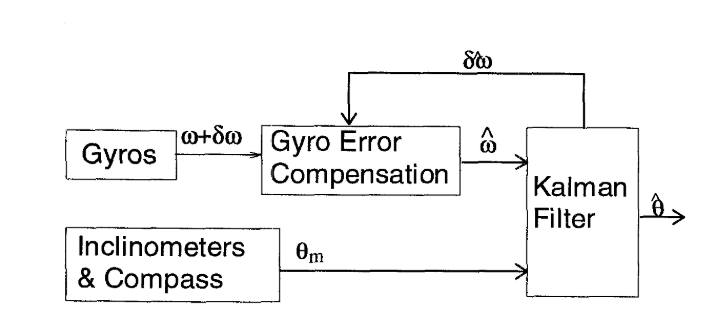
卡爾曼濾波的變種有哪些?4
基于擴展卡爾曼濾波的機動目標航跡跟蹤
卡爾曼濾波(KF)與擴展卡爾曼(EKF)
基于擴展卡爾曼濾波EKF的無感控制+Matlab/Simulink仿真案例




 卡爾曼濾波的總結和思維擴展
卡爾曼濾波的總結和思維擴展
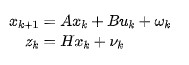
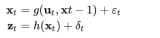










評論