3.1 背景
為什么需要定義一種“新”的變換?
計算機處理的兩個基本條件:第一,只能處理離散的數據(時域和頻域都要離散);第二,要有限長。
DTFT,時域上離散,但頻域是連續的;DFS,時域頻域都是離散的,但同時又都是周期的,周期序列長度為無限長。但同時我們也注意到,周期序列實際上只有有限個序列值有意義,因而它的離散傅里葉級數也適用于有限長序列,這就得到有限長序列的離散傅里葉變換(DFT)。
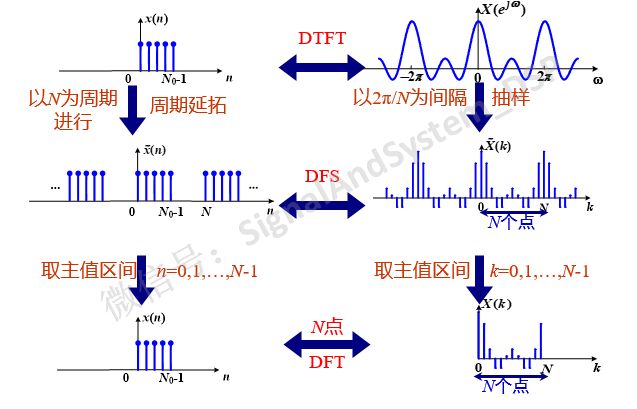
所以, DFT并不是一種新的變換 。它只是將DFS時域和頻域上都取一個周期而已。**DFT正反變換的定義式與DFS相同,只是加了一個取值范圍的限定而已。**換湯不換藥。
3.2 DFT的定義及物理含義
重點:DFT與DFS、DTFT的關系


DFT不是序列x(n)的真正的頻譜。x(n)的真正的頻譜是DTFT,DFT只是對其真正頻譜的一個周期上的離散抽樣值。
3.3 DFT的計算
重點:DFT的兩種計算方法。

下面的例題,分別用這兩種方法進行求解。


對于本題來說,方法二特別直觀,便于理解DFT與DTFT的關系。

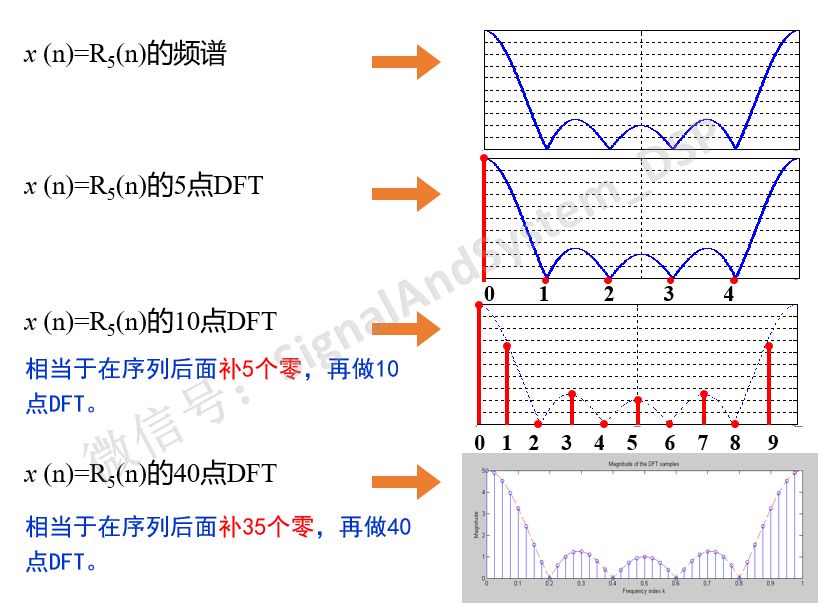
可見,同一個序列的不同點數的DFT,得到的結果不同。DFT的點數N越大,X(k)越能反映連續頻譜的形狀。
當DFT的點數N>序列的長度N0時,相當于在序列后面補上N-N0個零,故稱為” 補零DFT “。
-
計算機
+關注
關注
19文章
7513瀏覽量
88162 -
DFT
+關注
關注
2文章
231瀏覽量
22756 -
頻譜儀
+關注
關注
7文章
340瀏覽量
36090 -
DFS
+關注
關注
0文章
26瀏覽量
9172 -
離散傅里葉變換
+關注
關注
0文章
27瀏覽量
7170
發布評論請先 登錄
相關推薦




 離散傅里葉變換DFT的定義及計算方法
離散傅里葉變換DFT的定義及計算方法










評論