什么是微分代數方程?
微分代數方程是一類微分方程,其中一個或多個因變量導數未出現在方程中。方程中出現的未包含其導數的變量稱為代數變量,代數變量的存在意味著不能將這些方程記為顯式形式 y′=f(t,y)。
ode15s 和 ode23t 求解器可以使用奇異質量矩陣 M(t,y)y′=f(t,y) 來解算微分指數為1的線性隱式問題,包括以下形式的半顯式 DAE
y′0=f(t,y,z)
0 =g(t,y,z)
在此形式中,由于主對角線存在一個或多個零值,因此代數變量的存在會產生奇異質量矩陣。

默認情況下,求解器會自動檢驗質量矩陣的奇異性,以檢測 DAE 方程組。如果提前知道奇異性,則可將 odeset 的 MassSingular 選項設為 'yes'。對于 DAE,還可以使用 odeset 的 InitialSlope 屬性為求解器提供 y′(0) 的初始條件估計值。
舉個例子
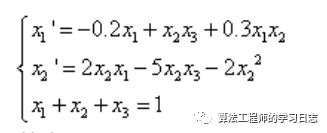
其中x1(0)=0.8;x2(0)=x3(0)=0.1;
1)方程寫成DAE形式
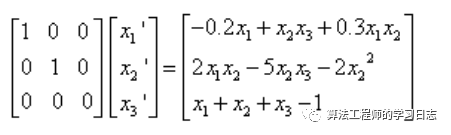
2)編程求解
%%
clc
clear
close all
odefun = @(t,x)[-0.2*x(1)+x(2)*x(3)+0.3*x(1)*x(2);
2*x(1)*x(2)-5*x(2)*x(3)-2*x(2)^2;
x(1)+x(2)+x(3)-1]; %微分方程
M = [1 0 0;0 1 0;0 0 0]; % 質量矩陣
options=odeset('mass',M); % 定義mass屬性
x0=[0.8;0.1;0.1];
[t,x]=ode15s(odefun,[0 10],x0,options);
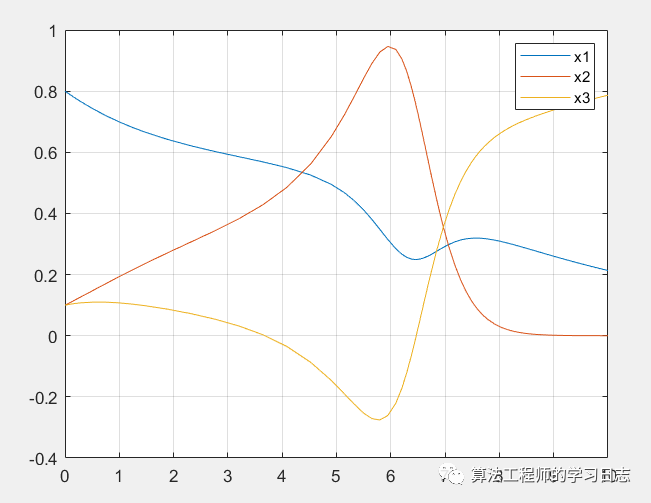
figure
plot(t,x(:,1),t,x(:,2),t,x(:,3))
grid on
legend('x1','x2','x3')
-
MATLAB仿真
+關注
關注
4文章
176瀏覽量
20401 -
MATLAB命令
+關注
關注
0文章
3瀏覽量
5118 -
MATLAB函數
+關注
關注
0文章
4瀏覽量
5255 -
求解器
+關注
關注
0文章
82瀏覽量
4766
發布評論請先 登錄
Matlab偏微分方程工具箱應用說明
Matlab求解微分方程(ODEs/PDEs)
Matlab的微分、積分和微分方程
改進LS方法降維電力系統常微分方程的研究
Matlab揭秘PDF中文版電子書免費下載

Matlab揭秘PDF電子書免費下載

進行線性代數方程組的數值實驗資料說明
微分方程的算子形式和拉普拉斯變換式之間的是什么關系?
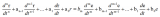




















評論