PSO（粒子群算法）在處理連續問題上有著較強的能力，因此很適合用來做參數優化，而PID控制器由三個參數組成，它們分別是：Kp 、Ki 、Kd 。

我們可以把PID控制器當做一個“黑箱”，輸入為這三個參數，輸出為響應曲線，我們要做的就是優化這個響應曲線。而一個控制效果好的PID控制器應針對不同類型輸入都有較快的響應速度，較小的超調以及穩態誤差。在本次分享中，選擇輸入信號為階躍輸入用來衡量PID控制效果。

PSO的適應函數選用綜合指標來衡量設計效果，由于是數字控制器，我們選用求和而不是積分的方式：

在特定的問題中，這個適應函數也可以按照實際需求修改，比如分析超調量、穩定時間等，具體問題具體分析

PSO的主函數和之前的案例類似

參數設置

wmax = 1;     % 最大慣性因子 
wmin = 0.6;   % 最小慣性因子 


% w = 0.6;      % 慣性因子 
c1 = 2;       % 加速常數
c2 = 2;       % 加速常數


Dim = 3;            % 維數
SwarmSize = 30;    % 粒子群規模
ObjFun = @PSO_PID;  % 待優化函數句柄


MaxIter = 10;      % 最大迭代次數  
MinFit = 0.1;       % 最小適應值 


Vmax = 1;
Vmin = -1;
Ub = [300 300 300];
Lb = [0 0 0];

其中的Ub和Lb分別是kp ki kd的上下限，開始優化的時候可以設置大一點，如果大概知道范圍，也可以縮小范圍，減少迭代次數

粒子群初始化

Range = ones(SwarmSize,1)*(Ub-Lb);
Swarm = rand(SwarmSize,Dim).*Range + ones(SwarmSize,1)*Lb;      % 初始化粒子群
VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin;                 % 初始化速度
fSwarm = zeros(SwarmSize,1);
for i=1:SwarmSize
    fSwarm(i,:) = PSO_PID(Swarm(i,:));                         % 粒子群的適應值
end


%% 個體極值和群體極值
[bestf,bestindex]=min(fSwarm);
zbest=Swarm(bestindex,:);   % 全局最佳
gbest=Swarm;                % 個體最佳
fgbest=fSwarm;              % 個體最佳適應值
fzbest=bestf;               % 全局最佳適應值

迭代尋優

iter = 0;
y_fitness = zeros(1,MaxIter);   % 預先產生4個空矩陣
K_p = zeros(1,MaxIter);         
K_i = zeros(1,MaxIter);
K_d = zeros(1,MaxIter);
while( (iter < MaxIter) && (fzbest > MinFit) )
    w = wmax-(wmax-wmin)/MaxIter*iter;  %% 慣性權重因子調整
    for j=1:SwarmSize
        % 速度更新
        VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
        if VStep(j,:) >Vmax, VStep(j,:)=Vmax; end
        if VStep(j,:)< Vmin, VStep(j,:)=Vmin; end
        % 位置更新
        Swarm(j,:)=Swarm(j,:)+VStep(j,:);
        for k=1:Dim
            if Swarm(j,k) >Ub(k), Swarm(j,k)=Ub(k); end
            if Swarm(j,k)< Lb(k), Swarm(j,k)=Lb(k); end
        end
        % 適應值
        fSwarm(j,:) = PSO_PID(Swarm(i,:));
        % 個體最優更新     
        if fSwarm(j) < fgbest(j)
            gbest(j,:) = Swarm(j,:);
            fgbest(j) = fSwarm(j);
        end
        % 群體最優更新
        if fSwarm(j) < fzbest
            zbest = Swarm(j,:);
            fzbest = fSwarm(j);
        end
    end 
    iter = iter+1;                      % 迭代次數更新
    y_fitness(1,iter) = fzbest;         % 為繪圖做準備
    K_p(1,iter) = zbest(1);
    K_i(1,iter) = zbest(2);
    K_d(1,iter) = zbest(3);
end

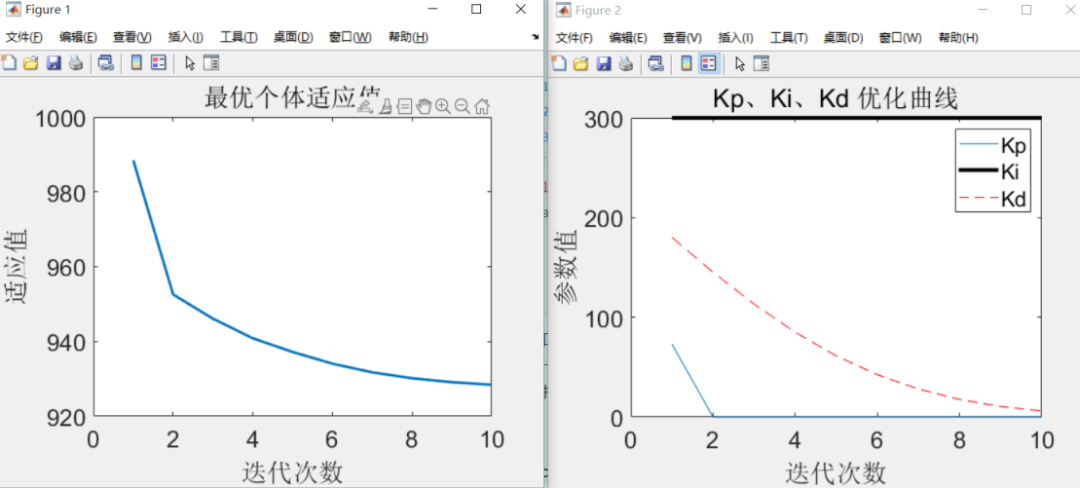
繪圖輸出

figure     % 繪制性能指標ITAE的變化曲線
plot(y_fitness,'LineWidth',2)
title('最優個體適應值','fontsize',18);
xlabel('迭代次數','fontsize',18);ylabel('適應值','fontsize',18);
set(gca,'Fontsize',18);


figure      % 繪制PID控制器參數變化曲線
plot(K_p)
hold on
plot(K_i,'k','LineWidth',3)
plot(K_d,'--r')
title('Kp、Ki、Kd 優化曲線','fontsize',18);
xlabel('迭代次數','fontsize',18);ylabel('參數值','fontsize',18);
set(gca,'Fontsize',18);
legend('Kp','Ki','Kd');

目標函數設計

function z=PSO_PID(x)
assignin('base','Kp',x(1));    %粒子依次賦值給Kp
assignin('base','Ki',x(2));    %粒子依次賦值給Ki
assignin('base','Kd',x(3));    %粒子依次賦值給Kd
try  %% simulink仿真異常，返回一個極大值
    y_out=sim('PID_Model',[0,20]);    %使用命令行運行控制系統模型
    z = y_out.yout{1}.Values.Data(end);
catch
    z=1e6;
end

代碼中assignin實現了m文件和simulink傳遞參數，其中y_out是simulink輸出的目標變量，為啥這兒需要一個try呢，因為這個優化的過程中，可能參數設置不合理，會拋出simulink報錯，故增加一個try避免代碼異常出錯提前結束優化過程

simulink模型用一個簡單的pid控制帶時延的傳遞函數

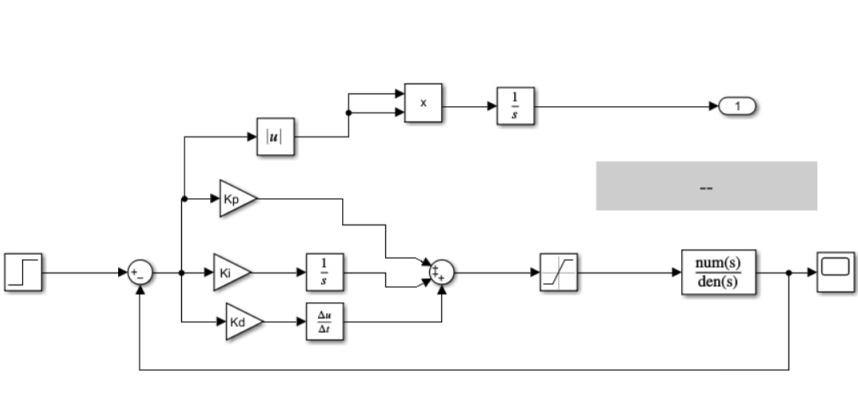
仿真結果類似這樣，因為迭代次數很少，設計中可以加大，得到更優的結果