• 多項式及函數

1.多項式的表示

MATLAB用一維向量來表示多項式，如多項式

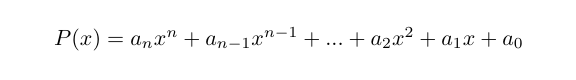
表示為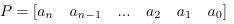,缺少的冪次系數用‘0’補充

2.多項式求根

求多項式的根即求使多項式為0的值，也即數學中的零點問題，MATLAB提供了 roots函數求根 ，用法如下：

>> P=[1 2 1];%x^2+2x+1=0
 >> roots(P)
ans =
    -1
    -1

根據多項式的根反求多項式則用 poly函數 ,一般多項式是行向量，根是列向量，例如：

> > r=[-1;-1];
 > > poly(r)
ans =
     1     2     1

3.多項式四則運算

加法：如果兩個多項式大小相同時，則多項式相加與標準的數組加法相同

乘法：使用conv函數

除法：使用 deconv函數 ，[a,r]=deconv(b,c)其中a為b除c的商，r為余數

>> a=[1 1];b=[1 -1];%(x+1)*(x-1)
 >> c=conv(a,b)
c =
     1     0    -1
 >> a=[1 3 1];b=[1 1];%x^2+3x+1除x+1
 >> [c,d]=deconv(a,b)
c =
     1     2
d =
     0     0    -1

4.多項式的導數、積分及其計算

導數：函數polyder可以實現多項式的求導

積分：函數 polyint(P,k) 返回多項式P的積分,積分常數項為k，默認值為0

計算：函數 polyval(P,x) 返回多項式在x處的值，x可為標量也可為向量

>> a=[1 2 1];polyder(a)
ans =
     2     2
 >> a=[1 2 1];b=polyder(a)
b =
     2     2
 >> polyint(b,3)
ans =
     1     2     3
 >> polyval(a,1)
ans =
     4

5.有理多項式

函數 [r,p,k]=residue(num,den) 可執行部分分式展開的的運算，等式兩邊互換可實現逆運算

> > num=[2 -19 29 40];
 > > den=[1 -15 68 -96];
 > > [r p k]=residue(num,den)
r =
    4.0000
    5.0000
    2.0000
p =
    8.0000
    4.0000
    3.0000
k =
     2

本例結果可表示為：

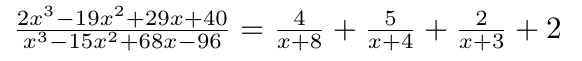
• 數據插值

數據插值是指數據缺失時所進行的一種處理，在數據分析、圖像處理等很多領域經常用到，參加過數學建模比賽的小伙伴可能也用過，有多項式插值、分段插值、三角函數插值等。

1. 一維函數插值

當插值函數y=f(x)一元函數時為一維插值，使用interp1函數，語法格式為 **Vq=interp1(X,V,Xq,str)** :X為自變量取值范圍，V為函數值或一向量，長度與X一致，Xq為插值點向量，str為字符串變量，設定插值方法。

str='nearest'： 鄰近點插值 。插值點的值為與該插值點最近的數據點函數值。速度快但平滑性差。

str='linear'： 線性插值法 。根據相鄰數據點的線性函數估計插值點的值。占用的 內存比鄰近點多，運算時間長 ，但其結果是連續的，頂點處斜率會改變。

str='spline'： 三次樣條插值 。在相鄰數據點建立三次多項式函數確定插值。運算時間最長，但平滑性最好。此外還有'pchip'，'cubic'，'v5cubic'等。

y=interpft(x,n) 為一維快速傅里葉插值。當數據點呈現周期分布時，用傅里葉變換把輸入數據x變換到頻域，然后用更多點n的傅里葉逆變換變回時域，其結果是對數據進行增采樣。

x=0:10;
y=sin(x);
z=interpft(y,20);
xx=linspace(0,10,20);%生成0到10之間20個線性等分點
plot(x,y,'-o',xx,z,':o')
legend('原始數據','插值結果','Location','North')

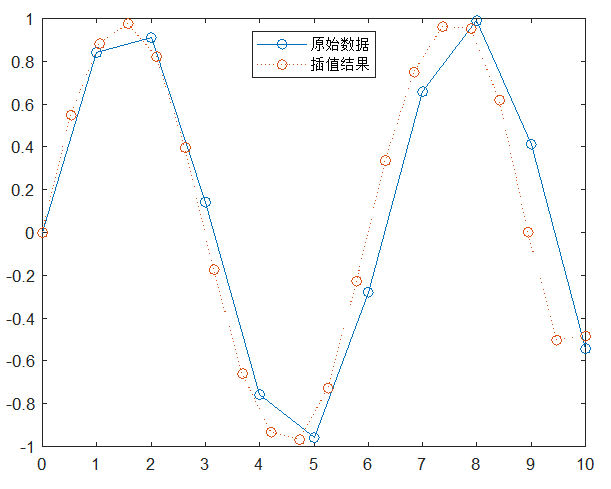
2.二維數據插值

當插值函數y=f(x)為二元函數時為二維插值，語法格式為 **Vq=interp2(X,Y,V,Xq,Yq,str)** 其中X,Y,V是具有相同大小的矩陣，V(i,j)是數據點[X(i,j),Y(i,j)]上的函數值；Xq,Yq為待插值數據網格，str為字符串變量表示不同的插值方法，和一維的相似，例如

[X,Y]=meshgrid(-10:0.25:10);%產生數據柵格點
Z=peaks(X,Y);  %計算已知點的函數值
[x,y]=meshgrid(-10:0.05:10); %產生更精密的插值點
z=interp2(X,Y,Z,x,y);
mesh(X,Y,Z),hold on;
mesh(x,y,z+20),hold off;
axis([-3 3 -3.5 3.5 -6 30])

• 函數極限

極限概念很簡單，在中學時就有所接觸，這里只簡單介紹一些使用極限的函數

limit(fun,x,a) ：當x趨于a時，返回函數fun的極限值。

limit(fun)：默認當x趨于0時求極限

limit(fun,x,a,'left') ：求左極限，還有右極限'right'

• 函數積分

MATLAB支持三重及以下的積分運算

1. 一重積分

一元函數的數值積分有三個函數quad, quadl, quadv用法相同

[Q,num]=quad(fun,a,b,tol,str) fun為被積函數句柄，a,b為積分上限和積分下限，tol用于控制誤差，增大tol可加快計算速度但精度下降，str非0時輸出計算過程中的[num a b-a Q]，num為函數計算的次數。此函數適用于精度低、被積函數平滑性較差的數值積分。num,tol,str為可選參數

quadl適用于精度高被積函數較平滑的數值積分

quadv用于被積函數是一些列函數的積分

2.二重積分

Q= dbquad (fun,xmin,xmax,ymin,ymax,tol,@quad)

Q=dbquad(fun,xmin,xmax,ymin,ymax,tol,myfun)

MATLAB默認采用quad函數計算一維積分；@quad表示用戶指定采用quadl函數來計算一維積分；myfun表示用自己編寫的一維積分函數

3.三重積分

Q= triplequad (fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,@quad)后面兩個參數為可選項