層次分析法(Analytic Hierarchy Process)是美國運籌學家薩蒂于上世紀70年代初,為美國國防部研究“根據各個工業部門對國家福利的貢獻大小而進行電力分配”課題時,提出的一種層次權重決策分析方法。其主要思想是根據研究對象的性質將要求達到的目標分解為多個組成因素,并按組成因素間的相互關系層次化,組成一個層次結構模型,然后按層分析,最終獲得最高層的重要性權值,其求解過程可以分為以下四步。
1.建立層次結構模型
將所包含的問題分層,可劃分為最高層、中間層、最低層。最高層表示需要解決問題的目的,也稱目標層。中間層表示實現總目標而采取的各種政策,一般分為策略層、約束層、準則層。最低層用于解決問題的各種措施、方案等,也稱措施層、方案層。利用層次分析建立選課的結構層次模型如下:
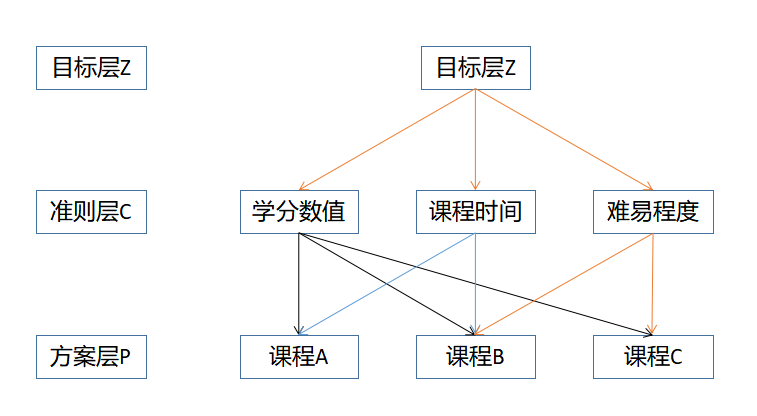
2.構造判斷矩陣
由于實際問題的諸多因素通常不易定量的測量,只能根據經驗與知識進行判斷,一種簡單的方法就是兩兩因素進行比較,從而提高判斷的精確性。描述因素相互影響大小的取值也做某種量化,取值為1到9, 的取值可以理解為因素 i 對目標層的影響程度是因素 j 的影響程度的多少倍,或因素 i 對因素 j 的重要程度,矩陣元素的取值及含義如下表:
的取值可以理解為因素 i 對目標層的影響程度是因素 j 的影響程度的多少倍,或因素 i 對因素 j 的重要程度,矩陣元素的取值及含義如下表:

根據上表可得準則層對目標層的判斷矩陣A(記為Z-A)

稱上述矩陣為正互反矩陣,即aii=1,aij=1/aji。
3.層次單排序及一致性檢驗
在構造判斷矩陣過程中,aij的取值僅注意了ai與aj對目標值的影響,而在確定矩陣各個元素時所采取的標準可能不一致。例如a12=2表示因素a1對目標層的影響是因素a2的2倍,a23=2表示因素a2對目標層的影響是因素a3的2倍,按常推理則a13=4,由于各種實際因素及主觀原因確定的a13不等于4,因而需要對矩陣進行一致性檢驗來盡量減少這種人為主觀上的不一致。若正互反矩陣滿足:

則稱為一致陣,其性質有:
(1)矩陣的秩即rank(A)=1
(2)矩陣的最大特征根為n,其余特征根為0
(3)最大特征根對應的特征向量
由判斷矩陣計算被比較元素對于該準則的相對權重,來確定每個因素的排序,稱為層次單排序。當考慮的因素較多時,很難保證判斷矩陣為一致陣,需要檢驗矩陣的一致性。令

CI為一致性指數,當CI=0,矩陣為一致陣,CI越大,矩陣不一致程度越大,但對單一的一個矩陣很難說其一致性指數的大小,因而又提出了平均隨機一致性指標RI檢驗判斷矩陣是否滿足一致性,對于判斷矩陣的階數n,RI取值如下表

令
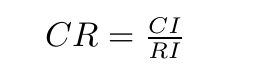
CR為隨機一致性比率,當CR<0.1時,判斷矩陣有滿意的一致性,否則要重新調整判斷矩陣使其通過一致性檢驗(注意各行成正倍數),才可以計算層次單排序的權重。
4.層次總排序及一致性檢驗
計算同一層次所有因素對于總目標相對重要性的排序權值的過程稱為層次總排序,計算和檢驗都是從最高層向最低層進行的。計算過程為:假設上一層次A一共包含m個因素 ,它的層次總排序權值分別為
,它的層次總排序權值分別為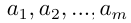 ,下一層次B包含n個因素
,下一層次B包含n個因素 它們對于Aj的層次單排序分別為
它們對于Aj的層次單排序分別為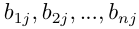 (當
(當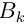 與
與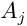 無聯系時
無聯系時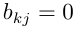 ),此時B層次總排序權值由下表給出:
),此時B層次總排序權值由下表給出:
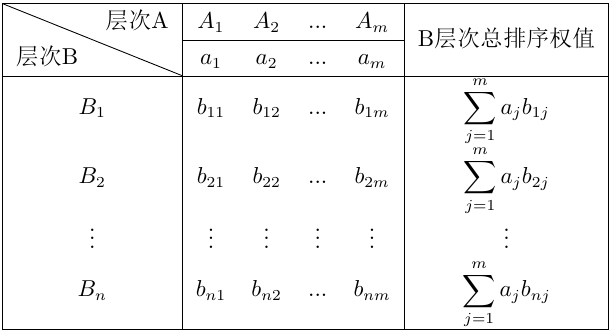
計算中間部分權值時按列看,可以理解為準則層B各因素對目標層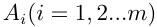 的相對權重;在計算B層次總排序相對權值時按行看,可以理解為
的相對權重;在計算B層次總排序相對權值時按行看,可以理解為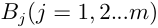 對上一層各因素的權值乘對應因素層次總排序權值的和。層次總排序也要進行一致性檢驗。設B層中的因素對
對上一層各因素的權值乘對應因素層次總排序權值的和。層次總排序也要進行一致性檢驗。設B層中的因素對 單排序的一致性檢驗為
單排序的一致性檢驗為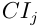 平均隨機一致性指標為
平均隨機一致性指標為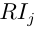 ,則B層次總排序隨機一致性比率CR為:
,則B層次總排序隨機一致性比率CR為:
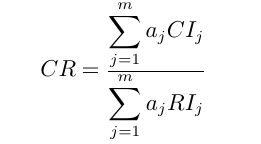
當CR<0.1時,層次總排序結果具有滿意的一致性
5.示例
通過前面的層次模型建立判斷矩陣后,并通過一致性檢驗后得準則層各因素對目標層的權值,及其一致性指數CI=0.054
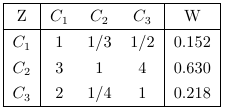
然后構造方案層對準則層的判斷矩陣C1-P、C2-P、C3-P,及其一致性指數分別為0.019,0,0
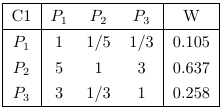
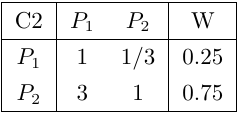
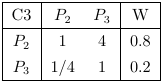
最后寫出各方案即課程對選課層的層次總排序表
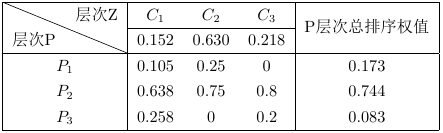
由于準則層各判斷矩陣階數分別為3,2,2,則由前表得RI值分別為0.58,0,0進行總排序一致性檢驗


從而CR=CI/RI=0.0332<0.1,滿足一致性檢驗,所以課程A,B,C的權值分別為0.173,0.744,0.083,得最終選擇課程B最優。從上述例子可以看出判斷矩陣的構建很關鍵,要通過專家打分環節獲得判斷矩陣,一般通過經驗判斷、多人評審或參考文獻等途徑獲得。
AHP源代碼
clear;clc;
Z=[1 1/3 1/2;3 1 4;2 1/4 1]; %準則層C對目標層Z的判斷矩陣
[CI0,Qz]=ahp(Z);
C1=[1 1/5 1/3;5 1 3;3 1/3 1];C2=[1 1/3;3 1];C3=[1 4;1/4 1];%方案層P對目標層Ci的判斷矩陣
[CI1,Qc1]=ahp(C1);
[CI2,Qc2]=ahp(C2);
[CI3,Qc3]=ahp(C3);
%計算層次總排序權值
P1=Qz(1,1)*Qc1(1,1)+Qz(2,1)*Qc2(1,1)+Qz(3,1)*0;
P2=Qz(1,1)*Qc1(2,1)+Qz(2,1)*Qc2(2,1)+Qz(3,1)*Qc3(1,1);
P3=Qz(1,1)*Qc1(3,1)+Qz(2,1)*0+Qz(3,1)*Qc3(2,1);
%總排序一致性檢驗
CI=Qz(1,1)*CI1+Qz(2,1)*CI2+Qz(3,1)*CI3;
RI=Qz(1,1)*0.58+Qz(2,1)*0+Qz(3,1)*0;
CR=CI/RI;
if CR >=0.1
error('沒有通過總排序一致性檢驗');
else
fprintf('通過總排序一致性檢驗n');
end
%% 通過判斷矩陣求權值函數
function [CI,Q]=ahp(B)
%CI為一致性指數,Q為權值,B為判斷矩陣
[n,m]=size(B);
%判別矩陣具有完全一致性
for i=1:n
for j=1:m
if B(i,j)*B(j,i)~=1
fprintf('i=%d,j=%d,B(i,j)=%d,B(j,i)=%dn',i,j,B(i,j),B(j,i));
error('判斷矩陣不具有完全一致性');
end
end
end
%求特征值特征向量,找到最大特征值對應的特征向量
[V,D]=eig(B); %V是特征向量, D是由特征值構成的對角矩陣,A*V=V*D。
tz=max(D); %返回的行向量為矩陣每一列的最大值
tzz=max(tz); %返回行向量的最大值
c1=find(D==tzz); %find返回一個包含數組D中每個非零元素的線性索引的向量,由于D為對角矩陣這里返回值為tzz的索引。
tzx=V(:,c1);%特征向量
%權值
Q=zeros(n,1);
for i=1:n
Q(i,1)=tzx(i,1)/sum(tzx);
end
%計算權值還可以用算術平均法和幾何平均法
%一致性檢驗
CI=(tzz-n)/(n-1);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判斷是否通過一致性檢驗
CR=CI/RI(1,n);
if CR >=0.1
error('沒有通過一致性檢驗');
else
fprintf('通過一致性檢驗n');
end
end
-
向量機
+關注
關注
0文章
166瀏覽量
21236 -
AHP
+關注
關注
0文章
9瀏覽量
8569 -
功率矩陣
+關注
關注
0文章
2瀏覽量
1375
發布評論請先 登錄
怎樣分析一個網站的權重
裝備維修優化的決策分析
質量管理與決策分析學
基于比較可能度的屬性權重未知的多屬性決策方法
一種漏洞威脅基礎評分指標權重分配方法
一種多屬性匹配決策方法
自適應系統決策:一種模型驅動的方法
一種多階段多屬性的匹配決策方法
一種新的DEA公共權重生成方法
一種層次結構中多維屬性的可視化方法
一種約束權重的改進多目標跟蹤方法
一種基于用戶偏好的權重搜索及告警選擇方法









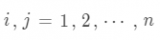











評論