正文

然后看到這篇關(guān)于浮點(diǎn)數(shù)的文章，希望大家看了之后有所啟發(fā)。

想一下，為什么第一個(gè)打印的和預(yù)設(shè)值不同，但是第二個(gè)是相同的？

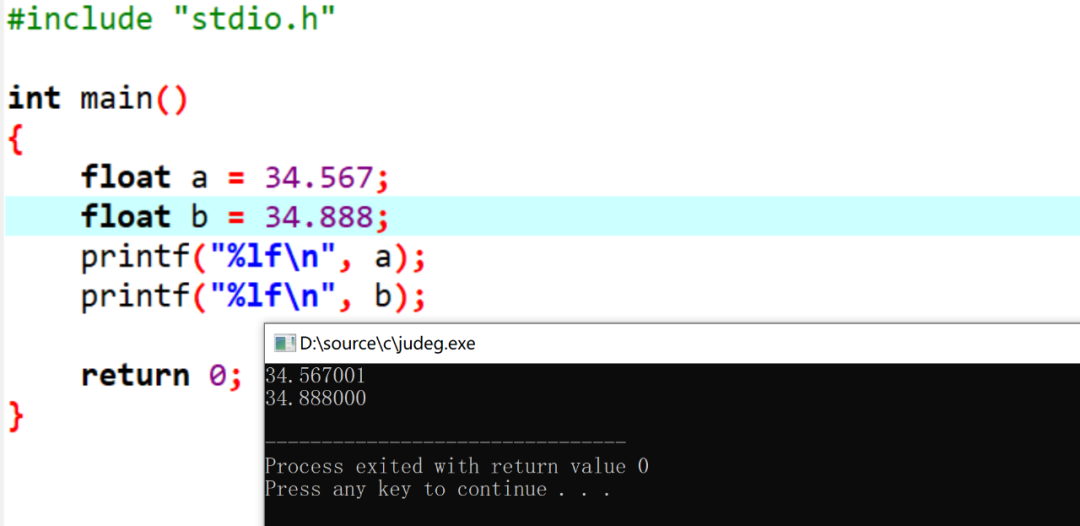
如圖：

尾數(shù)部分是如何轉(zhuǎn)變成二進(jìn)制的？

前言

很多人在初學(xué)寫(xiě)程式時(shí)都會(huì)遇到所謂的浮點(diǎn)誤差，如果你到目前都還沒(méi)被浮點(diǎn)誤差雷過(guò)，那只能說(shuō)你真的很幸運(yùn)XD。

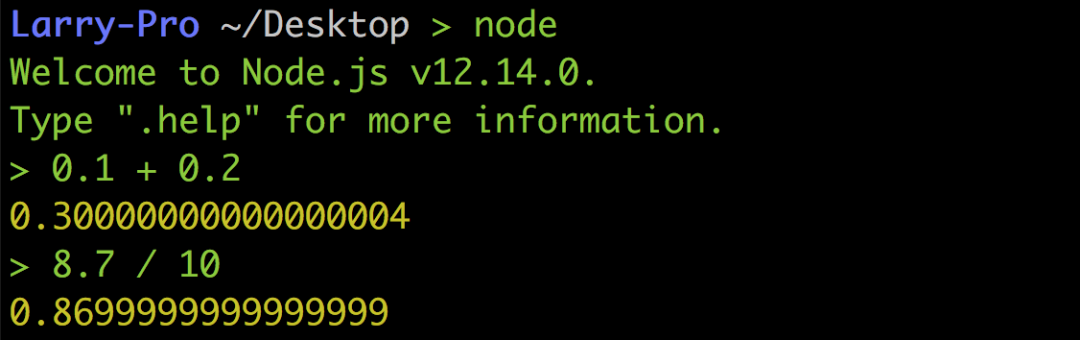
以下圖Python 的例子來(lái)說(shuō)0.1 + 0.2并不等于0.3，8.7 / 10也不等于0.87，而是0.869999…，真的超怪der

但這絕對(duì)不是什么神bug，也不是Python 設(shè)計(jì)得不好，而是浮點(diǎn)數(shù)在做運(yùn)算時(shí)必然的結(jié)果，所以即便是到了Node.js 或其他語(yǔ)言也都是一樣。

電腦如何儲(chǔ)存一個(gè)整數(shù)(Integer)

在講為什么會(huì)有浮點(diǎn)誤差之前，先來(lái)談?wù)勲娔X是怎么用0 跟1 來(lái)表示一個(gè)整數(shù)，大家應(yīng)該都知道二進(jìn)制這個(gè)東西：像101代表22 + 2? 也就是5、1010代表23 + 21 也就是10。

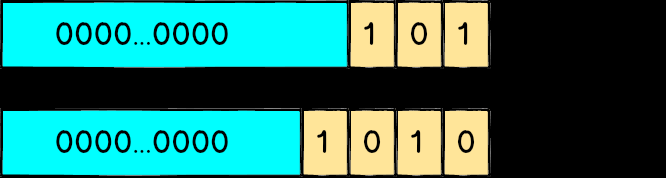
如果是一個(gè)unsigned 的32 bit 整數(shù)，代表他有32 個(gè)位置可以放0 或1，所以最小值就是0000...0000也就是0，而最大值1111...1111代表231 + 23? + … + 21 + 2? 也就是4294967295。

從排列組合的角度來(lái)想，因?yàn)槊恳粋€(gè)bit 都可以是0 或1，整個(gè)變數(shù)值有232 種可能性，所以可以精確的表達(dá)出0 到232-1 中任一個(gè)值，不會(huì)有任何誤差。

浮點(diǎn)數(shù)(Floating Point)

雖然從0 到232-1 之間有很多很多個(gè)整數(shù)，但數(shù)量終究是有限的，就是232 個(gè)那么多而已；但浮點(diǎn)數(shù)就大大的不同了，大家可以這樣想：在1 到10 這個(gè)區(qū)間中只有十個(gè)整數(shù)，但卻有無(wú)限多個(gè)浮點(diǎn)數(shù)，譬如說(shuō)5.1、5.11、5.111 等等，再怎么數(shù)都數(shù)不完。

但因?yàn)樵?2 bit 的空間中就只有232 種可能性，為了把所有浮點(diǎn)數(shù)都塞在這個(gè)32 bit 的空間里面，許多CPU 廠(chǎng)商發(fā)明了各種浮點(diǎn)數(shù)的表示方式，但若各家CPU 的格式都不一樣也很麻煩，所以最后是以IEEE發(fā)布的IEEE 754作為通用的浮點(diǎn)數(shù)運(yùn)算標(biāo)準(zhǔn)，后來(lái)的CPU 也都遵循這個(gè)標(biāo)準(zhǔn)進(jìn)行設(shè)計(jì)。

IEEE 754

IEEE 754 里面定義了很多東西，其中包括單精度（32 bit）、雙精度（64 bit）跟特殊值（無(wú)窮大、NaN）的表示方式等。

正規(guī)化

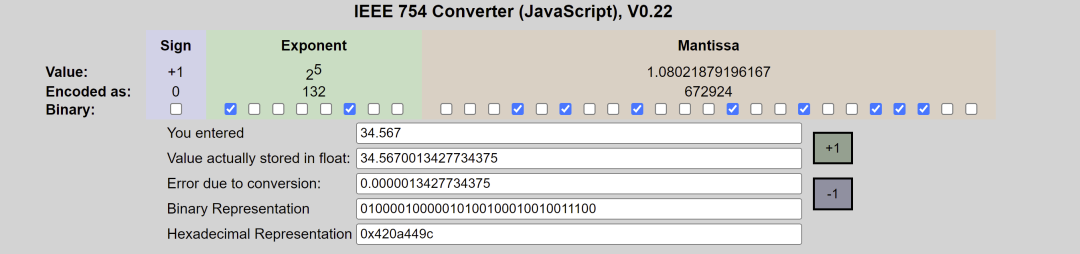
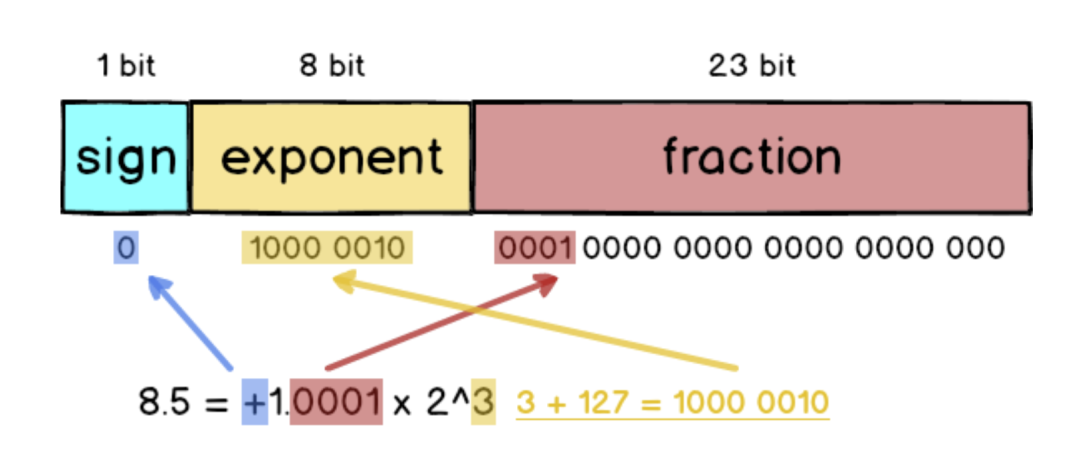
以8.5 這個(gè)符點(diǎn)數(shù)來(lái)說(shuō)，如果要變成IEEE 754 格式的話(huà)必須先做正規(guī)化：把8.5 拆成8 + 0.5 也就是23 + 1/21，接著寫(xiě)成二進(jìn)位變成1000.1，最后再寫(xiě)成1.0001 x 23，跟十進(jìn)位的科學(xué)記號(hào)滿(mǎn)像的。

單精度浮點(diǎn)數(shù)

在IEEE 754 中32 bit 浮點(diǎn)數(shù)被拆成三個(gè)部分，分別是sign、exponent 跟fraction，加起來(lái)總共是32 個(gè)bit。

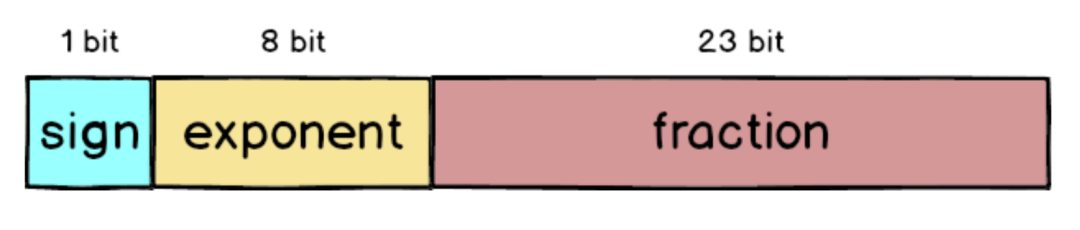
sign：最左側(cè)的1 bit 代表正負(fù)號(hào)，正數(shù)的話(huà)sign 就為0，反之則是 1。

exponent：中間的8 bit 代表正規(guī)化后的次方數(shù)，采用的是超127格式，也就是3 還要加上127 = 130。

fraction：最右側(cè)的23 bit 放的是小數(shù)部分，以1.0001 來(lái)說(shuō)就是去掉1. 之后的000。

所以如果把8.5 表示成32 bit 格式的話(huà)就會(huì)是這樣：

這圖我畫(huà)超久的，請(qǐng)大家仔細(xì)看XD。

什么情況下會(huì)不準(zhǔn)呢？

剛剛8.5 的例子可以完全表示為23+ 1/21，是因?yàn)? 跟0.5 剛好都是2 的次方數(shù)，所以完全不需要犧牲任何精準(zhǔn)度。

但如果是8.9 的話(huà)因?yàn)闆](méi)辦法換成2 的次方數(shù)相加，所以最后會(huì)被迫表示成1.0001110011… x 23，而且還會(huì)產(chǎn)生大概0.0000003 的誤差，好奇結(jié)果的話(huà)可以到IEEE-754 Floating Point Converter網(wǎng)站上玩玩看。

雙精度浮點(diǎn)數(shù)

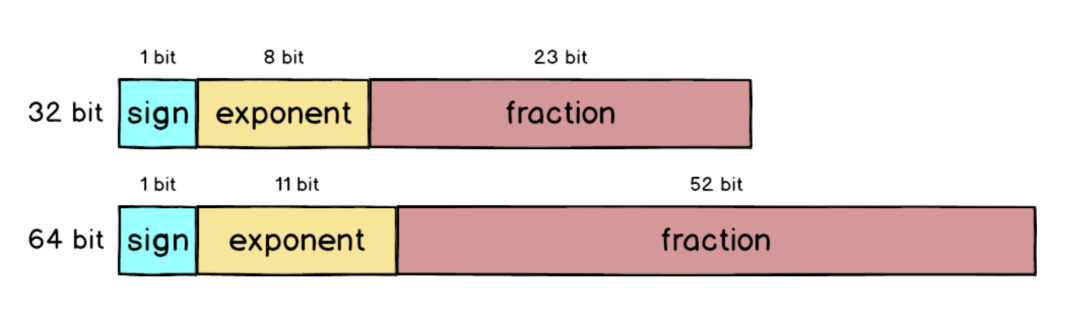
上面講的單精度浮點(diǎn)數(shù)只用了32 bit 來(lái)表示，為了讓誤差更小，IEEE 754 也定義了如何用64 bit 來(lái)表示浮點(diǎn)數(shù)，跟32 bit 比起來(lái)fraction 部分大了超過(guò)兩倍，從23 bit 變成52 bit，所以精準(zhǔn)度自然提高許多。

以剛剛不太準(zhǔn)的8.9 為例，用64 bit 表示的話(huà)雖然可以變得更準(zhǔn)，但因?yàn)?.9 無(wú)法完全寫(xiě)成2 的次方數(shù)相加，到了小數(shù)下16 位還是出現(xiàn)誤差，不過(guò)跟原本的誤差0.0000003 比起來(lái)已經(jīng)小了很多。

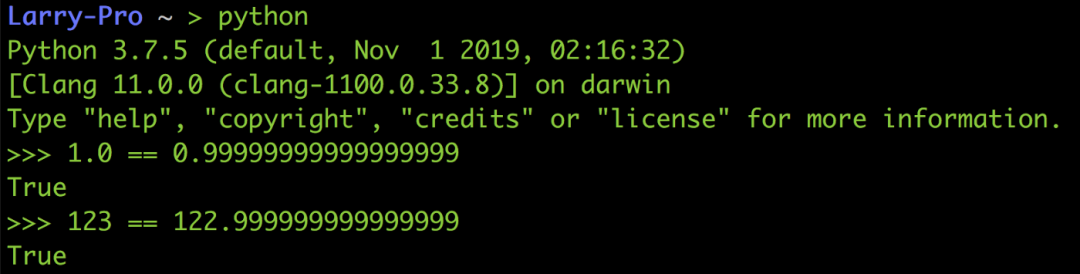
類(lèi)似的情況還有像Python 中的1.0跟0.999...999是相等的、123跟122.999...999也是相等的，因?yàn)樗麄冎g的差距已經(jīng)小到無(wú)法放在fraction 里面，所以就二進(jìn)制的格式看來(lái)他們每一個(gè)bit 都一樣。

解決方法

既然無(wú)法避免浮點(diǎn)誤差，那就只好跟他共處了（打不過(guò)就加入？），這邊提供兩個(gè)比較常見(jiàn)的處理方法。

設(shè)定最大允許誤差ε (epsilon)

在某些語(yǔ)言里面會(huì)提供所謂的epsilon，用來(lái)讓你判斷是不是在浮點(diǎn)誤差的允許范圍內(nèi)，以Python 來(lái)說(shuō)epsilon 的值大概是2.2e-16。

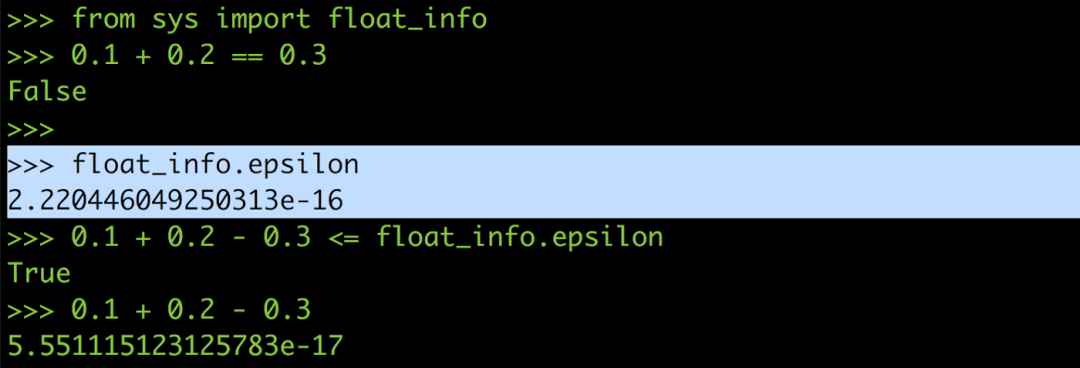
所以你可以把0.1 + 0.2 == 0.3改寫(xiě)成0.1 + 0.2 — 0.3 <= epsilon，這樣就能避免浮點(diǎn)誤差在運(yùn)算過(guò)程中作怪，也就可以正確比較出0.1 加0.2 是不是等于0.3。

當(dāng)然如果系統(tǒng)沒(méi)提供的話(huà)你也可以自己定義一個(gè)epsilon，設(shè)定在2 的-15 次方左右。

完全使用十進(jìn)位進(jìn)行計(jì)算

之所以會(huì)有浮點(diǎn)誤差，是因?yàn)槭M(jìn)制轉(zhuǎn)二進(jìn)制的過(guò)程中沒(méi)辦法把所有的小數(shù)部分都塞進(jìn)fraction，既然轉(zhuǎn)換可能會(huì)有誤差，那干脆就不要轉(zhuǎn)了，直接用十進(jìn)制來(lái)做計(jì)算！！

在Python 里面有一個(gè)module 叫做decimal，它可以幫你用十進(jìn)位來(lái)進(jìn)行計(jì)算，就像你自己用紙筆計(jì)算0.1 + 0.2 絕對(duì)不會(huì)出錯(cuò)、也不會(huì)有任何誤差（其他語(yǔ)言也有類(lèi)似的模組）。

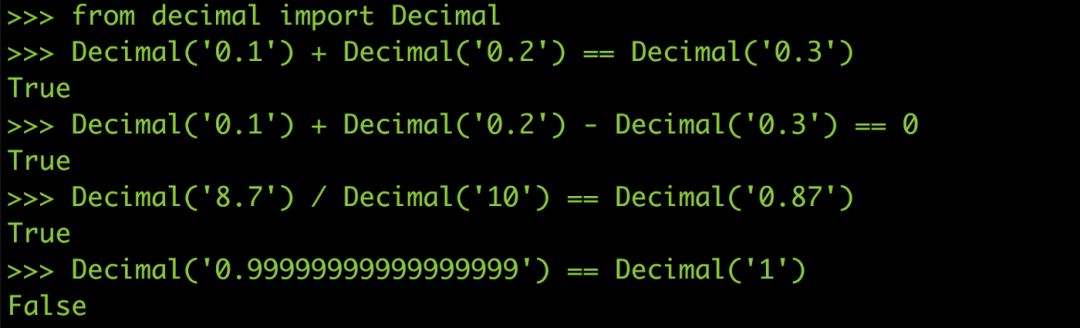
自從我用了Decimal 之后不只bug 不見(jiàn)了，連考試也都考一百分了呢！

雖然用十進(jìn)位進(jìn)行計(jì)算可以完全躲掉浮點(diǎn)誤差，但因?yàn)镈ecimal 的十進(jìn)位計(jì)算是模擬出來(lái)的，在最底層的CPU 電路中還是用二進(jìn)位在進(jìn)行計(jì)算，所以跑起來(lái)會(huì)比原生的浮點(diǎn)運(yùn)算慢非常多，所以也不建議全部的浮點(diǎn)運(yùn)算都用Decimal 來(lái)做。

總結(jié)

回歸到這篇文章的主題：「為什么浮點(diǎn)誤差是無(wú)法避免的？」，相信大家都已經(jīng)知道了。

至于你說(shuō)知道IEEE 754 的浮點(diǎn)數(shù)格式有什么用嗎？好像也沒(méi)什么特別的用處XD，只是覺(jué)得能從浮點(diǎn)數(shù)的格式來(lái)探究誤差的成因很有趣而已，感覺(jué)離真相又近了一點(diǎn)點(diǎn)。

而且說(shuō)不定哪天會(huì)有人問(wèn)我「為什么浮點(diǎn)運(yùn)算會(huì)產(chǎn)生誤差而整數(shù)不會(huì)」，那時(shí)我就可以有自信的講解給他聽(tīng)，而不是跟他說(shuō)「反正浮點(diǎn)運(yùn)算就是會(huì)有誤差，背起來(lái)就對(duì)了」

來(lái)源：https://medium.com/starbugs/see-why-floating-point-error-can-not-be-avoided-from-ieee-754-809720b32175 版權(quán)歸原作者或平臺(tái)所有，僅供學(xué)習(xí)參考與學(xué)術(shù)研究，如有侵權(quán)，麻煩聯(lián)系刪除~感謝

審核編輯：劉清