回顧計算機中的數字
在學習計算機基礎的過程中我們已經知道計算機是基于二進制對數據進行存儲和運算的。學習C語言時我們又知道了C語言中常見的數據類型有:char,int,long int等 signed 或 unsigned 整數數據,以及float和double型的小數數據。
或看過我之前文章的朋友肯定也明白了,無論使用何種語言編寫的何種程序,最后進入處理器執行的都是一串二進制數據,是不是突然又想不明白處理器到底是怎么區分這些數據類型了?這不又繞回原來說的底層邏輯了嗎,你學微機原理,學匯編指令不就是幫你解決這個問題的?回過頭去研究明白了那以后何止單片機軟件開發呢,芯片設計,系統、編譯器開發不都能勝任了。扯遠了,先回到正題。

對于帶小數的數據也是如此,同樣需要將十進制數據轉為二進制,并規定其符號位,指數位以及小數位。比如IEEE.754標準(即IEEE二進制浮點數算術標準)中對float,double存儲邏輯的規定:
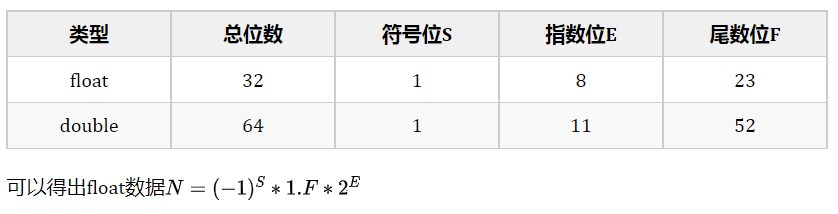
定點數據
一般情況下我們會將有小數的數據稱為浮點型數據,float為單精度浮點數據,double為雙精度浮點數據。正如上面所說的我們計算機使用的是以浮點法保存小數型數據的。與之對應的肯定就會有以定點的方式保存小數數據的方法。
定點是指表示一個數值時,小數點之后的位數是固定的,有時候小數點之前的位數是固定的。上面用浮點表示的小數,小數點的位置不是固定的,可以根據有效位數而浮動。

浮點數與定點數表示

定點小數

定點整數
定點數類型的值其實就是個整數,需要額外做比例進位,進多少位需要根據具體的定點數類型決定。例如 1.23 使用 1/1000 縮放系數的定點數表示時是 1230;1,230,000 使用 1000 縮放系數的定點數表示也是 1230。與浮點數不同,相同類型的定點數中所有值的縮放系數都是一致的,在計算過程中也保持不變。此表示法可以用標準的整數算術邏輯單元來進行有理數的計算。
為了效率考量,縮放系數(scaling factor)一般會是基數b(2 或是 10)的正冪次,或是負冪次,因此實際內部仍然可以用類似整數的方式處理。不過縮放系數也需依應用而定。因此許多的數字可能其數值其實是用二進制記錄,但為了使用方便人類讀寫,縮放系數仍選擇10的冪,10的冪的縮放系數也可以配合國際單位制,因為選擇特定的縮放系數,可能相當于使用另外一個大小較適合的單位,例如使用厘米或微米,而不是使用米,或者是以1/3600為縮放系數的定點數來表示以小時為單位的時間值,精確到秒。
采用定點計數法時,相鄰兩個數之差總是等于其中一個數的值,而采用浮點計數法時,相鄰數并不是均勻分布的。另外浮點計數的計數范圍是比定點計數范圍要大得多,并且一般場景中浮點計數精度往往也比定點計數精度高,正因為如此,一般情況下浮點計數法更適合于一般應用場景,一般老師在課堂上也不會做詳細介紹,所以我們對定點數感到陌生也完全不奇怪。
所以現在大多數處理器芯片都是帶有浮點運算器(FPU),只有在特殊的應用中才使用定點數運算,例如某些特定應用下的數字信號處理芯片(DSP)或一些低價的嵌入式系統微處理器(MCU),這類的應用強調高需求速度,低電力需求及小集成電路區域,例如影像、視頻或圖片等數字信號處理,進行傅里葉變換以及數字濾波器設計,或是其他一些這種數字表示法比較適合的場景,如貨幣計算,儀器測量計數等,這些都是有特定的精度規則,使用浮點計數反而可能帶來更大的芯片資源消耗或成本開支,并且這些情況運算速度也不如定點運算快。


當然平時使用時我們也可以編寫一些特定程序對這些格式表示的數值范圍進行驗證。
#include < stdio.h >
#include < stdint.h >
#include < math.h >
int main()
{
int16_t q_max = 32767; // 0x7FFF
int16_t q_min = -32768; // 0x8000
float f_max = 0;
float f_min = 0;
printf("rn");
for (int8_t i = 15; i >=0; i--)
{
f_max = (float)q_max / pow(2,i);
f_min = (float)q_min / pow(2,i);
printf("t|Q%dt|Q%d.%dt|%ft|%ft|rn",
i,(15-i),i,f_max,f_min);
}
return 0;
}

定點與浮點相互轉化
在一些功能復雜的處理器中會同時支持兩種數據處理方式,比如STM32G4系列的芯片上攜帶的FMAC(filtermath accelerator)支持的定點DSP處理功能,使用的定點格式為Q1.15。
在這種既有定點運算又有浮點運算是處理器上做開發時我們不可避免的都會涉及到定點與浮點相互轉化的問題,這時需要注意進行處理數據!

定點運算思的擴展
在某些特定情況下定點運算對算法的效率優化有著出奇的效果,如果你對這方面感興趣不妨可以研究一下經典的快速平方根算法。
另外,我們平時做單片機開發時在一些比較低端的芯片中,比如C51單片機,請切記不要輕易使用浮點運算!如果需要進行小數運算,我們可以借助定點運算是思想在程序中通過設計一定的比例系數對數據進行放大或縮小處理,從而實現某些功能。不要問我為啥,舉個簡單的例子,利用超聲波模塊測距,你自己寫兩個程序,一個使用浮點,一個不使用做個實驗測試一下就可以知道結果是怎么的了。
-
STM32
+關注
關注
2295文章
11033瀏覽量
365482 -
C語言
+關注
關注
180文章
7633瀏覽量
141963 -
信號處理器
+關注
關注
1文章
258瀏覽量
25782 -
傅里葉變換
+關注
關注
6文章
443瀏覽量
43161 -
浮點運算器
+關注
關注
0文章
4瀏覽量
5822
發布評論請先 登錄
【安富萊——DSP教程】第7章 DSP定點數和浮點數(重要)
第7章 DSP定點數和浮點數
請問28335浮點數使用IQmath轉換后當定點數計算快還是用浮點數進行計算快?28335可以定點浮點混合編程嗎?
6618虛擬定點數學庫IQmath
verilog程序定點數的資料
DSP功能函數-定點數互轉
在定點數運算中產生溢出的原因是什么
定點數和浮點數的區別是什么
請問ADSP-21469的匯編指令集ISA/VISA中有沒有專門用來進行浮點數和定點數轉換的指令?
LabVIEW中定點數有什么用途?LabVIEW中定點數應用解析
在FPGA里浮點數與定點數表示法原理展示

定點數和浮點數在STM32單片機中使用傅里葉(FFT)變換的理解

FPGA定點數截位的基本準則



















評論