 關鍵要點
關鍵要點
將復雜的電路理解為串聯和并行連接的組合。
線性的概念及其在電路分析中的應用。
用來快速有效地表示等效電路的附加方法。
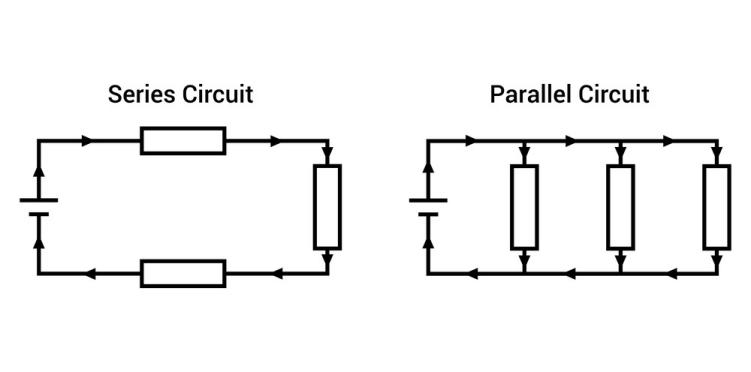
復雜電路包括串聯和并聯元件,在這里分別顯示
電路設計是一門廣泛的學科,它結合了許多數學分析和電磁學的方法。在該理論發展的早期,設計師會遇到電路的基本構建模塊以及電路簡化的入門協議。雖然這些是電路的基礎,并且幾乎適用于任何電路,但還有很多情況需要更復雜的描述。復雜的電路提供了一個額外的挑戰,因為它們需要更高級的技術才能得到一個可以通過人類或機器進行分析的網絡。學習這些程序為設計師提供了更多的電路分析機制,并更全面地理解了網絡設計。
 節點分析:串聯和并聯連接
節點分析:串聯和并聯連接
在任何新興工程師的工具箱中,等效電路簡化都是最重要的解決方法之一。將復雜電路網絡簡化為單一的代表性電路元件的能力是電路建模和分析的核心方法。首先,定義電路拓撲的一個基本方面十分重要:串聯和并聯。理解這些相關概念的最佳方法是跟蹤電流的流動:
串聯:電流流經電路中的元件時,它們會連成一條線,沒有任何分支。換句話說,該特定電路或子電路中不存在分支電流路徑。在網絡分析方面,連續串聯的元件共享一個節點或參考點。
并聯:電流從源頭分配到多個分支路徑上。對于任何有兩個端口的并聯元件,兩個節點都與其它并聯的兩個端口元件共通。
除了基礎電路之外, 幾乎很少有完全串聯或并聯的整體電路。相反, 大多數電路包含不同數量的串聯和并聯元件,以利用這兩種連接方法的不同性能特征。復雜的電路,或包含并聯和串聯元件的電路,更為常見。在分析方面,評估一個由串聯元件組成的電路通常比一個并行電路更直接,盡管這個規則有明顯的組件例外。大多數級數元素都是單個元素的總和——為了找到純級數網絡的阻力,只需添加循環中包含的值。平行元素的和不那么直觀:平行相加,取單個分量的倒數和的倒數。如所描述的串聯和并聯計算都適用于電阻器和電感器,但電容器是該框架的一個顯著的例外。雖然電容器確實有規律地和相互求和,但它們的應用是交換的:串聯電容器相互求和,而傳統的并聯電容器相互求和。在分析電路時,盡管有明顯的組件例外,評估由串聯元件組成的電路通常比并聯電路更為直觀。大多數串聯元件是各個元素的總和:要找到純串聯網絡的電阻,只需將循環內包含的值相加即可。并聯元件的總和則不那么直觀:要進行并聯,需要對各個組件的倒數之和取倒數。上述串聯和并聯計算適用于電阻器和電感器,但電容器則例外。雖然電容器通常可以進行常規的倒數求和,但它們的應用是相反的:串聯電容器進行倒數求和,而并聯電容器則進行常規求和。
 使用基爾霍夫定律進行節點分析
使用基爾霍夫定律進行節點分析
也可以從電壓和電流方面分析串聯和并行配置。串聯組件,作為同一分支,具有相同的電流,但在每個非源電路元件的電壓降,如基爾肖夫的環路定律概述。同時,由于基爾肖夫的結規則,并聯組件具有相同的電壓,但有不同的電流,即進入一個節點的總電流必須等于一個節點的總電流。更正式地說,串聯元件和并聯元件可以分別被描述為分壓器和分流器。這些電路操作根據組件的相對值提供電壓或電流的比例分布;例如,兩個相同的電阻會經歷相同的電壓降(串聯)或相同的電流(并聯),因為它們的電阻為1:1值。對于不同的值,較大(或最大)的元件代表電流或電壓的最大比例,反之亦然。在電路中,我們可以通過電壓和電流的角度來分析串聯和并聯配置。如基爾霍夫環路定律所述,串聯元件在同一電路中,擁有相同的電流,但每個非提供電流的電路元件都會產生一定的電壓降。與此同時,并聯元件擁有相同的電壓,但由于基爾霍夫節點定律所示,不同的電流會進入和流出節點,使它們的電流不同。從更正式的角度講,串聯和并聯元件可以被描述為電壓分壓器和電流分流器,分別提供基于元件相對值的電壓或電流的比例分配;例如,兩個相同的電阻器在串聯時將經歷相同的電壓降,而在并聯時將經歷相同的電流,因為它們具有1:1的電阻值。
 復雜電路簡化的構建
復雜電路簡化的構建
復雜性的話題需要與線性和疊加相結合。線性描述了系統的整體行為,即從輸入到輸出的映射,而疊加是線性系統的決定條件。為了保持疊加,系統必須在整個輸入范圍內維持可加性和齊次性:可加性 :兩個單獨輸入的組合輸出與組合輸入的總和輸出相同。更常見的是,可以表示為等式:
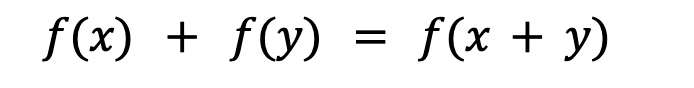
*假設x和y是f域內的元素。
齊次性:輸入端的標量乘以某個值,等價于輸出端相應標量乘以該值。同樣,這需要一個更常見的等式:
f (sx) = sf (x)
*對于所有元素s,x在f的域內。
回到一個電路的復雜性,疊加,特別是可加性特性,是一個系統的輸入和輸出之間的關系。復雜電路是并行元素和串聯元素的混合物,它們的解代表了這兩種連接方法的適當貢獻。為了進一步推動這種關系,復雜電路代表了平行和串聯元件的組成,在非正式和數學上;在節點分析的背景下,電氣工程師參考疊加理論,以區分更一般和數學的疊加原理的彎曲。這兩個元素的組合形成了疊加原理的基礎并定義了一個線性系統。總體而言,線性的適用范圍有限,是對系統真實行為的簡化,但在它適用的情況下,它是一種強有力的工具來建模。有利的是,線性系統可以用各種數學函數、變換和算子來分析,并且比非線性系統更容易求解。回到電路的復雜性,疊加原理,特別是可加性特性,是系統輸入和輸出之間的關系。如前所述,復雜電路是并聯和串聯元素的組合,并且它們的解決方案代表了兩種連接方法的結合。
 評估不那么直觀的網絡
評估不那么直觀的網絡
事實上,許多網絡可以通過串聯求和并行求和。人工分析應緩慢而仔細地進行,以確定兩個元素之間的關系,以及適當的順序,以在計算中保留串聯或并聯組件的性質。然而,并不是每一種電路排列都易于串聯或并聯的識別,需要利用各種轉換來更好地說明電路內的關系。一般來說,星形變換多邊形用于減少特定電路中的節點數量,盡管其實現有一個實際的限制,即元素的替換數量受到以下限制:
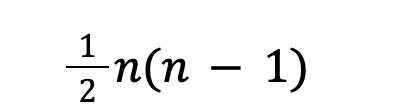
*對于n個元素數。
最有用的情況是當n = 3時,因為轉換后的網絡具有與原始網絡相同數量的元素,但也應該提到其他值。使用小于3個元素的轉換將生成具有更少組件的模型,而使用大于3個元素的轉換將增加組件的總數,同時減少節點數。前者的使用范圍有限,而后者只會使分析復雜化。回到特殊的n = 3的情況下,在一些情況下,設計師可能會遇到非正統的網絡結構。雖然在捕獲的示意圖中不太常見,但它們仍然可以在三個元素的節點交點上找到,比如在橋中發現的那些元素。這些轉換的形式上是基于網絡的視覺形狀的Y-Δ(delta)或T-π(pi)轉換,它們利用組件之間的級數和并行關系來創建所有三個元素之間的比例。刪除節點允許將電路重新解釋為串聯或并聯連接,進一步強調了在復雜電路分析中進行變換的優勢。

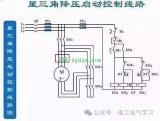
Δ-Y變換通常與三相電力系統有關
 進一步降低復雜性的等效電路模型
進一步降低復雜性的等效電路模型
復雜電路的簡化有時需要使用額外的算法來產生可工作的拓撲結構。最初為由電流源、電壓源和電阻器組成的線性直流電路設計的這兩種方法,可通常適用于固定頻率的線性交流電路:費溫定律:將電路替換為一個等效電壓源和串聯電阻,測量開路電壓。將電路轉換為費溫定理等效電路的三個步驟如下:
1. 確定等效電壓(Vth),即輸出端測量的電壓。通常,這是通過使用已知的源電壓和電壓分壓計算來確定留在輸出端的源電壓的分數來實現的。注意,打開電路(其中負載與等效電路隔離)會導致某些支路沒有電流流動。
2. 通過從輸出端子的電路來確定等效電阻(Rth)。這個電阻是通過假設所有電源的理想電阻,即電壓源的理想電阻為零,電流源的理想電阻為無窮大,并將它們分別替換為開路和短路。
3. 最后,費溫等效電路可以用Vth的電壓源和Rth的串聯電阻來表示。
Mayer-Norton電路理論-用等效電流源和并聯電阻(從負載角度)替代電路。作為Thévenin等效性的對立面,實現Mayer-Norton等效電路需要遵循三個步驟:
1.通過在負載處短路終端來找到等效電流(Ino)。首先找到總電流(通常使用歐姆定律,但其他方法也可獲得更快的結果)。一旦找到總電流,則計算輸出短路電流。
2.與Thévenin等效電路一樣,通過用短路和開路替換源,從輸出端評估等效電阻。
3.從負載處觀察,Mayer-Norton等效電路顯示為電流源Ino和并聯電阻Rth。
Thévenin和Mayer-Norton代表一種雙重方法,通常在電子學中看到,其中任一使用互補的模式提供等效性。盡管線性電路只占工程師和設計師將遇到的拓撲結構的一小部分,因為符合框架的設備數量有限,但等效電路具有相關源的附加用例。通常,當確定等效電壓或電流時,電壓和電流源將被替換為短路和開路,但不能輕易忽略相關源。相反,設計師可以將測試源連接到輸出端,并計算所得到的電流或電壓。
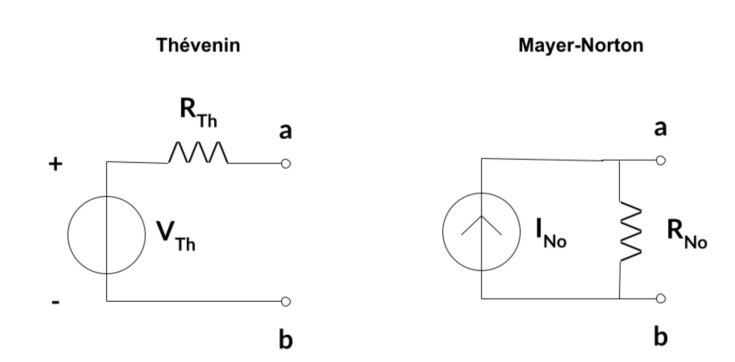
兩種等效電路模型的比較。
復雜電路簡化存在的目的是為工程師和設計師提供各種算法,以簡化電路設計過程。能夠用簡單的實踐方法測量廣泛網絡的響應,極大地提高了網絡分析的可讀性。此外,這些方法構成了電子節點分析的基礎,這對電路模擬非常必要。
Cadence的PCB設計和分析軟件提供了全面的設計和分析工具包,具備滿足最嚴格的板子規格的廣泛功能。對于布局,OrCAD PCB Designer提供了強大的功能,可以滿足當今全功能板的需求,并推動未來設計的創新。Cadence Allegro PCB Designer是一個完整的、高性能印制電路板設計套件。通過頂尖的技術,它為創建和編輯復雜、多層、高速、高密度的印制電路板設計提供了一個交互式、約束驅動的設計環境。它允許用戶在設計過程的任意階段定義、管理和驗證關鍵的高速信號,并能抓住今天最具挑戰性的設計問題。AllegroPCB Designer提高了設計效率和縮短設計周期,讓你的產品盡快進入量產。
-
電路
+關注
關注
172文章
5926瀏覽量
172353 -
電路分析
+關注
關注
62文章
518瀏覽量
98829 -
電路設計
+關注
關注
6676文章
2453瀏覽量
204492
發布評論請先 登錄
相關推薦
射頻分析儀的技術原理和應用場景
buck電路的穩定性分析方法
放大電路的基本分析方法有哪兩種
對放大電路的分析方法介紹
信號分析的方法有哪些
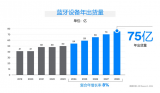
藍牙技術聯盟發布《2024年藍牙市場最新資訊》




 技術資訊 | 復雜電路分析與簡化方法
技術資訊 | 復雜電路分析與簡化方法











評論