我們知道,快速傅里葉變換 (FFT) 是信號處理的重要數(shù)學工具。一般而言,n點信號的離散傅里葉變換 (DFT) 的變換結果(頻域)也是n個數(shù)據(jù)點。但在實際應用中,對實際信號作FFT時,常常涉及到變換前數(shù)據(jù)需要補零 (Zero padding) 的問題。
一些論壇里,曾看到某些專業(yè)人士從信息論的角度分析認為:“Zero padding沒有增加時域信號的有效信息,因此,不會改變DFT/FFT的分辨率”。那么, 補零到底有什么用,什么時候需要補零呢? 對于一般的工程技術人員來說,基本就是調用現(xiàn)成代碼或模塊進行計算,很少考慮這些問題。其實,了解和搞清楚這個問題,對實際應用還是很有幫助的。接下來,我們將從以下幾個方面來簡要闡述如何補零,以及它對頻譜分析結果的影響。
什么是補零 ( Zero Padding )?
簡單來說,補零 (Zero Padding) 就是對變換前的時域或空域信號的尾部添加若干個0,以增加數(shù)據(jù)長度。如圖1所示,為含有1.00MHz和1.05MHz兩個頻率成分合成的正弦波實信號。
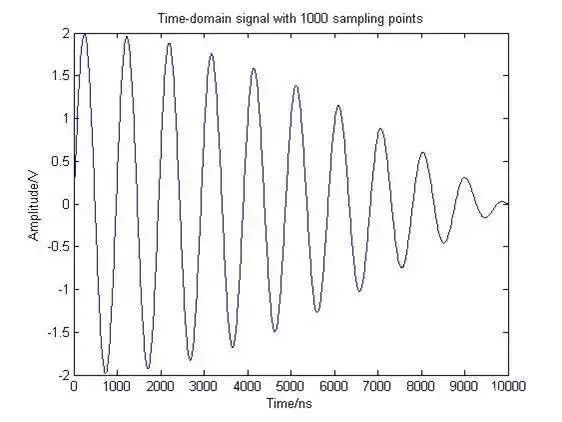
(a)
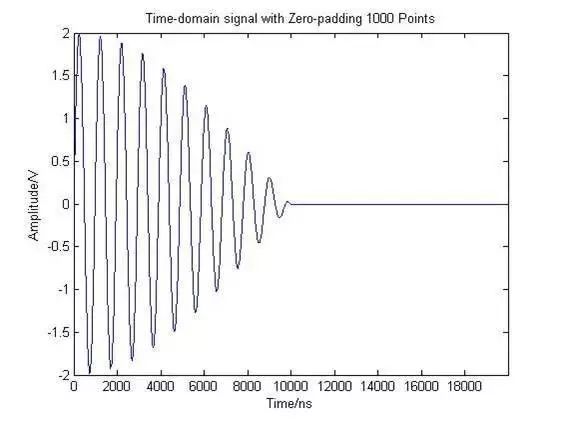
(b)
圖1 時域信號的補零示意圖
圖1(a)中信號長度為1000個樣點,采樣頻率為 fs =100MHz時,信號的實際時長則為10us。在其尾部添加1000個0,即數(shù)據(jù)增加到了2000個點(時長為20us),則變?yōu)閳D1(b)所示的波形。
這個過程就是通常所說的補零(ZeroPadding)。
為什么要Zero Padding?
最直接的理由就是,如果時域波形的數(shù)據(jù)樣點為2的整數(shù)冪的話,F(xiàn)FT計算將是最高效的,硬件 (FPGAs) 計算FFT,就是采用了這樣的Padding工作模式。那么,我們所關心的補零會不會影響計算輸出的頻率分辨率呢?
關于FFT頻率分辨率
這里涉及到兩種意義下的分辨率問題,一種叫“波形頻率分辨率 (Waveform frequency resolution”) 或叫視覺頻率分辨率 (Visual frequency resolution);另一種則叫做“FFT分辨率”。雖然,這個分類和命名不一定是很專業(yè)的術語,但卻有助于對“頻率分辨率”概念的理解。在沒有補零的情況下,這兩個概念通常容易被混淆,因為它們是等價的。
波形頻率分辨率是指可以被分辨的2個頻率的最小間隔 (Spacing);而FFT 分辨率則是頻譜中的數(shù)據(jù)點數(shù) (The number of points in the spectrum),它是與做FFT的點數(shù)直接相關的。
因此,波形頻率分辨率可定義為:
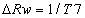
其中,T是實際信號的時間長度。
同樣,F(xiàn)FT分辨率可以定義為:
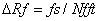
其中,fs為采樣頻率 (the sampling frequency),Nfft為FFT的點數(shù)。ΔRf代表了FFT頻率軸上的頻率取值的間隔 (Spacing)。
值得注意的是,可能有很好的FFT分辨率,但卻不一定能夠很好的把2個頻率成分簡單的分開。同樣,可能有很高的波形分辨率,但波形的能量峰值會通過整個頻譜而分散開(這是因為FFT的頻率泄漏現(xiàn)象)。
我們知道,信號的離散傅里葉變換 (DFT) 或快速傅里葉變換 (FFT) 是對波形的任何一邊補零形成的無限序列進行計算的。這就是,為什么FFT的每個頻率單元 (bin) 都具有明顯的sinc波的形狀。
波形頻率分辨率1/T與一個sinc函數(shù)空值間隔 (the space between nulls) 是一樣的。
例 析
下面以一個具有2種頻率成分的周期信號為例,說明Zero Padding與頻譜分辨率的關系:
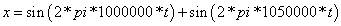
其中,f1 = 1.00MHz,f2 = 1.05MHz,頻率間隔為0.05MHz。也就是說,在我們的頻譜分析曲線上能看到2個頻率點的峰,若2個正弦波的幅度為1伏 ( V),那么我們期望在1MHz和1.05MHz的頻率點處的功率為10dBm。
分以下幾種情況進行分析:
1. 時域信號1000個點采樣,做相同樣點數(shù)的FFT。
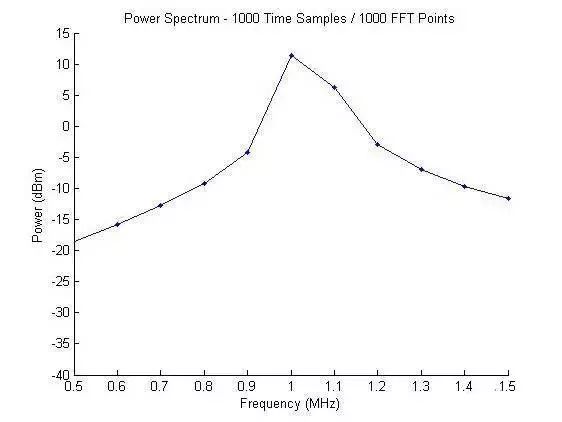
圖2 原始信號的功率譜 (1000點 FFT)
圖2中,我們并沒有看見期望的兩個脈沖,因為圖中僅出現(xiàn)一個脈沖點,其幅度約為11.4dBm。顯然,這個圖并不是我們想要的正確的頻譜圖。原因很簡單,沒有足夠的分辨率看見兩個峰值 (Peaks)。
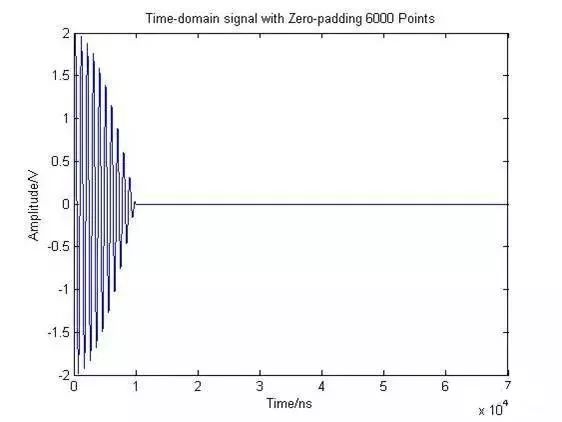
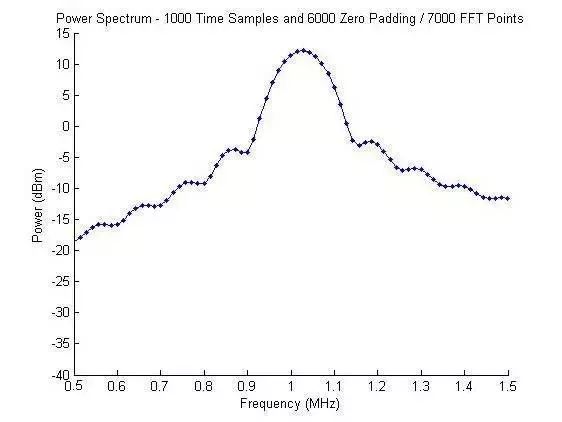
2. 時域信號1000個點采樣,后端補6000個零,做7000點數(shù)的FFT。
我們自然想到,采用補零方式增加FFT點數(shù),以使頻率軸上能增加更多點數(shù)。如采用7000個點做FFT,即需要在原1000點信號尾部增加6000個零值(即60us時長),則原始信號變?yōu)閳D3(a)所示,其FFT結果如圖3(b)所示。
(a)
(b)
圖3 原始信號補零及功率譜 (7000點 FFT)
圖3中,我們也并沒有看見期望的結果。仔細觀察一下,此圖到底告訴了我們什么呢?即通過增加更多FFT點數(shù)的做法,使得波形頻率分辨率公式中的sinc函數(shù)的定義更清晰。可以看出,sinc空值 (nulls) 間隔大約是0.1MHz。
由于給出信號的兩個正弦波的頻率間隔是按0.05MHz分隔的,因此,不管我們用多少FFT點數(shù) (Zero padding),都無法解決2個正弦波的問題。
再來看一下頻率分辨率ΔRf告訴了我們什么。盡管,F(xiàn)FT分辨率大約為14kHz(足夠的頻率分辨率),而波形頻率分辨率僅僅為100kHz。兩個信號的頻率間隔是50kHz,所以我們受限于波形頻率分辨率 ΔRw 。
3. 時域信號7000個點采樣,做7000點數(shù)的FFT。
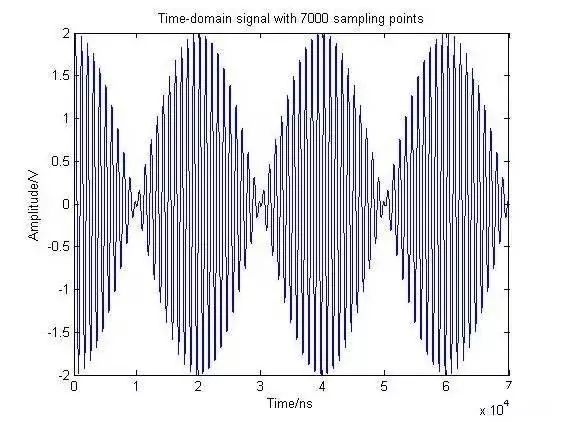
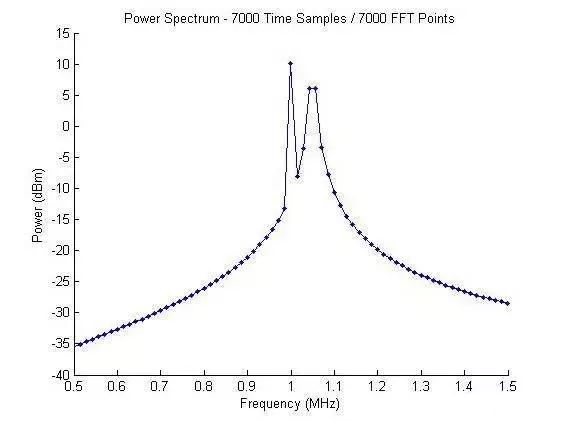
為了合理地解決這個頻譜的問題,需要增加用于FFT的時域數(shù)據(jù)的長度(點數(shù))。因此,我們直接采集波形的7000點作為輸入信號,取代補零 (Zero Padding) 方式到70us (7000 點) 。時間域信號及對應的功率譜分別如圖4a-4b所示。
(a)
(b)
圖4 按7000點采集的信號及其功率譜
通過時域數(shù)據(jù)的周期延拓,現(xiàn)在的波形頻率分辨率ΔRw也近似為14KHz。但從頻譜圖中,我們還是看不見2個正弦波。1MHz信號已按正確的10dBm功率值清晰地表征,而1.05MHz 信號變寬,且未以期望的10dBm 功率分布。這是為什么呢?
原因就是1.05MHz處并沒有FFT點的分布,此處的能量被多個FFT點分散(泄露)了。
給出的例子中,采樣頻率是100MHz,F(xiàn)FT點數(shù)為7000。頻譜圖中,點與點之間的間隔是14.28kHz。1MHz頻率剛好為頻率間隔的整數(shù)陪,而1.05MHz 卻不是。距1.05MHz最近的整數(shù)倍頻率為1.043MHz和1.057MHz,因此,能量被這2個FFT單元所分散。
4. 時域信號7000個點采樣,后端補1000個零,做8000點數(shù)的FFT。
為了解決這個問題,我們可以合理選擇FFT的點數(shù),以便這兩個點能在頻率軸上成為獨立分開的點。由于,我們并不需要更好的波形頻率分辨率,僅采用時域數(shù)據(jù)的零填充方式來調整FFT數(shù)據(jù)點的頻率間隔。
給時域信號增加1000零值 (10us),使得頻率間隔為12.5kHz,這樣,滿足了1 MHz and 1.05MHz兩個頻率都是這個間隔的整數(shù)倍。此時,給出的功率譜如圖5所示。可以看出,兩個頻率問題得到解決,而且功率均在期望的10dBm。
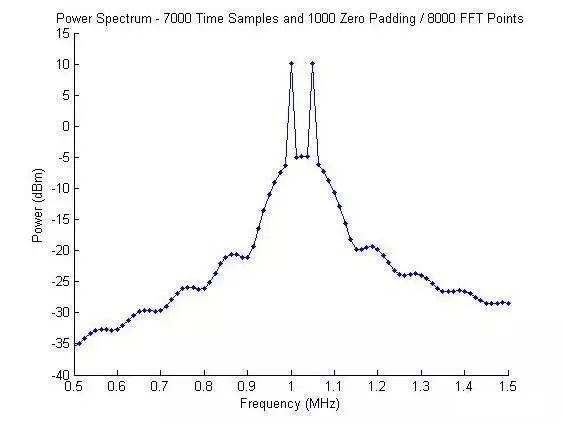
圖5 補零至8000點信號的功率譜
為了進一步觀察過度補零的現(xiàn)象,通過時域補更多的零值 (10000點) 來完成更多點數(shù)的FFT(確保具有正確的波形頻率分辨率 ΔRw ),我們就可以清晰地看到FFT單元 (bins) 的sinc波形狀,如圖6所示。
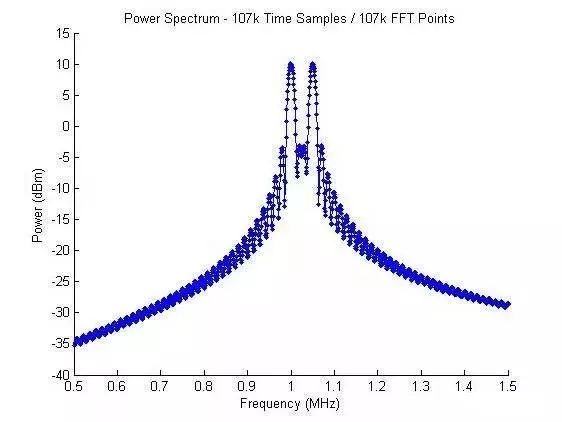
圖6 補零至107000點信號的功率譜
-
FFT
+關注
關注
15文章
434瀏覽量
59367 -
功率譜
+關注
關注
0文章
13瀏覽量
8343 -
信號處理器
+關注
關注
1文章
254瀏覽量
25272 -
時域分析
+關注
關注
0文章
35瀏覽量
11091 -
DFT算法
+關注
關注
0文章
27瀏覽量
7535
發(fā)布評論請先 登錄
相關推薦
新手一個,關于系統(tǒng)外擴8253接口電路,有個問題求教育==、
BLE一次廣播的字節(jié)數(shù)一定是32個嗎,剩余自動補零?
_SlNonOsMainLoopTask() 函數(shù)有什么用,什么時候調用?
調用STM32的DSP庫做fft運算補零是為了補充虛部嗎?
筆記本固態(tài)硬盤到底有什么用呢
異常處理向量表的設置中DCD這些偽指令到底有什么用?
為什么要用傅里葉變換?FFT你不知道的細節(jié)
關于賽靈思FPGA實現(xiàn)高效并行實時上采樣的分析和介紹
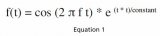
數(shù)據(jù)可視化到底有什么用?
關于FFT的信號補零操作




 傅里葉變換補零到底有什么用,什么時候需要補零呢?
傅里葉變換補零到底有什么用,什么時候需要補零呢?










評論