一、引言

系統數學模型時域表示：端口（輸入-輸出）描述（一元n階微分方程）與狀態方程描述（n元聯立一階微分方程）

二、系統數學模型（微分方程）的建立

建立方程式： 元件約束特性 + 網絡拓撲約束 （KVL+KCL）

三、用時域經典法求解微分方程

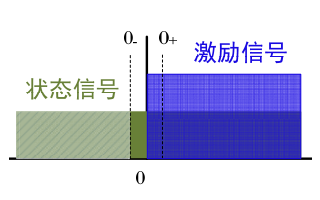
四、起始點的跳變——從0-到0+狀態的切換

五、零輸入響應與零狀態響應

六、沖激響應與階躍響應

七、卷積

八、卷積的性質

九、利用卷積分析通信系統多徑失真的消除方法

解卷積求出回波系統逆沖激響應函數→激勵卷積回波系統沖激響應函數卷積回波系統逆沖激響應函數=激勵本身

十、用算子符號表示微分方程

十一、總結

LTI 系統分析方法包括時間域和變換域兩方面的問題。時域直接求解系統微分、積分方程， 直觀且物理概念清晰 。系統數學模型的時域表示一般用端口描述與狀態方程描述的方法。本章主要介紹的是端口描述的方法。一般根據元件的約束特性和網絡拓樸約束構建系統的數學模型，即微分方程。可以采用 時域經典法 、零輸入零狀態法和卷積的方法來求解系統的微分方程。

時域經典法將微分方程的全解分解為齊次解與 特解 。采用高數所給結論求出解的形式并根據條件求出待定系數。根據其求解過程，齊次解與特解具有很清晰的物理意義： 齊次解對應完全由系統自身特性決定其形式（特征根與自然頻率）的自由響應 （求出形式及其特征根，當然最后的系數也要根據條件與激勵求出來）， 特解對應系統特性與外加激勵共同決定的強迫響應 。因此時域經典法具有清晰的物理概念，然而求解過程較為麻煩。同時，還需考慮 起始點的跳變 ，即0-到0+狀態的切換。 跳變由激勵的突然接入引起 。 起始狀態 （0-）表達的是 系統過去的信息 ， 初始狀態 （0+）表達的是 接入激勵后剛開始的初始條件 （作為求解微分方程的初始條件）。其可以根據 系統內部儲能的連續性 （電容與電感特性）或沖激函數匹配法來確定。

零輸入零狀態法則由上述起始條件與初始條件引出。 零輸入響應是沒有外加激勵信號，只由起始狀態（系統儲能）所產生的響應 ，沒有激勵的接入因此 不會產生跳變 。而 零狀態響應則不考慮起始時刻系統儲能的作用（認為原來系統沒有能量），由系統本身外加激勵信號所產生的響應 ，因此 可能發生跳變 （后面引入卷積后可以用卷積方法求解）。要注意自由響應與零輸入響應的區別。其 均滿足齊次方程的解 ，但 零輸入響應僅由系統結構和起始儲能狀態決定 ，而 自由響應的形式則由系統結構決定，其系數需要根據激勵信號和起始儲能狀態求出 。

卷積方法則是 將信號分解為沖激信號之和，借助系統沖激響應來求解系統對任意激勵信號的零狀態響應 。首先引入系統的 沖激響應 ，即單位沖激信號作為激勵，系統產生的 零狀態響應 （可見不考慮儲能）。根據 線性時不變系統的疊加原理 ，能夠得到系統接入不同激勵產生的零狀態響應（從δ(t)到e(t)，從h(t)到r(t)，推導過程就是卷積能夠求解零狀態的原因）。引入卷積能夠更方便地求解系統的 零狀態響應 （詳見第四章拉氏變換部分，根據數學推導，引入卷積能夠很巧妙地跳過起始條件到初始條件的繁瑣求解，將這一變化包含了進去）。卷積將一個函數拆分成一個個的沖激， 揭示了系統某一時刻的輸出是由無數個單一輸入共同作用（疊加）的結果 。而這種結果與之前所有時刻響應均有關的積分運算過程在信號處理上相當于一種 平滑與展寬的濾波 。卷積的詳細物理意義與應用見后續傅里葉變換與拉氏變換部分的介紹。