一、引言
時域研究——頻域研究
傅里葉級數——采用 三角函數系 ( 互為正交函數 )進行正交展開
二、周期信號的傅里葉級數分析

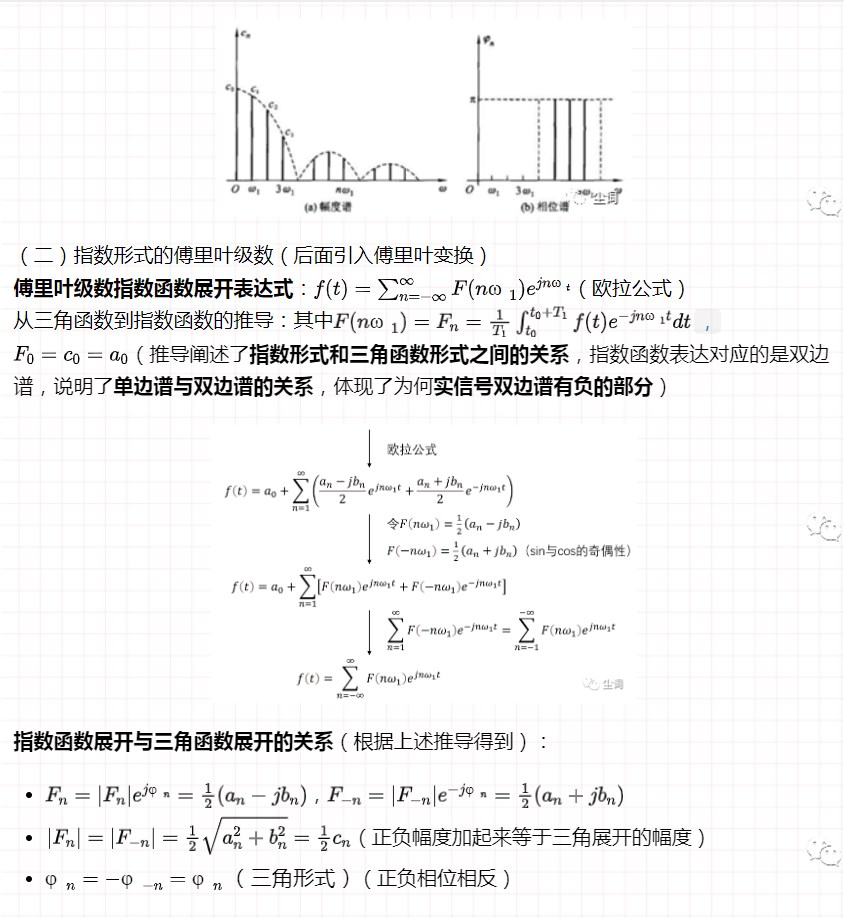


三、典型周期信號的傅里葉級數
(一)周期矩形脈沖信號
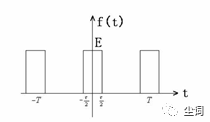
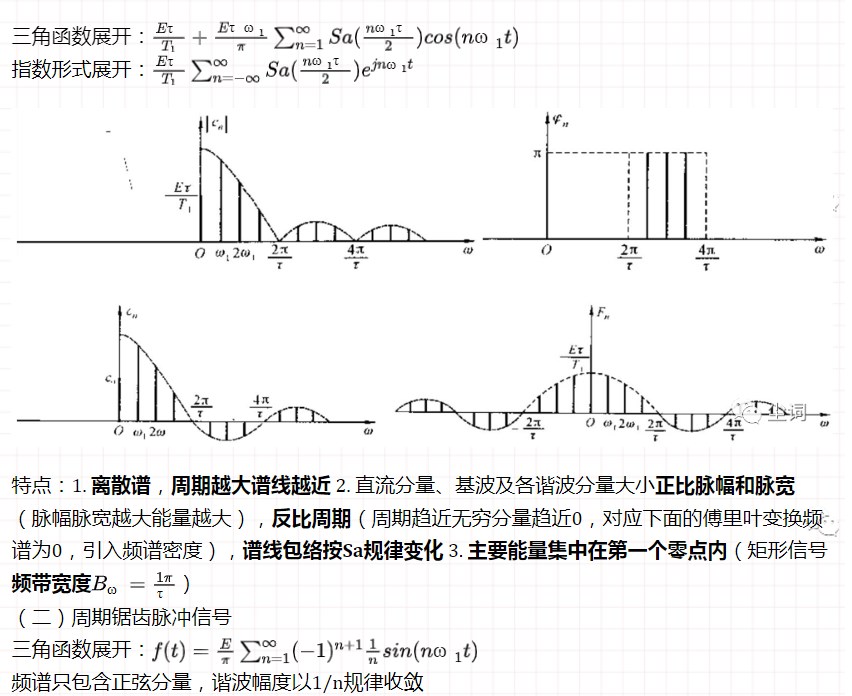

四、傅里葉變換
由傅里葉級數引出傅里葉變換:T→∞時,譜線間隔趨于0,值趨于無限小,由能量守恒得無限多無限小能量之和仍為信號的能量,此時頻譜失去意義,故引入頻譜密度函數
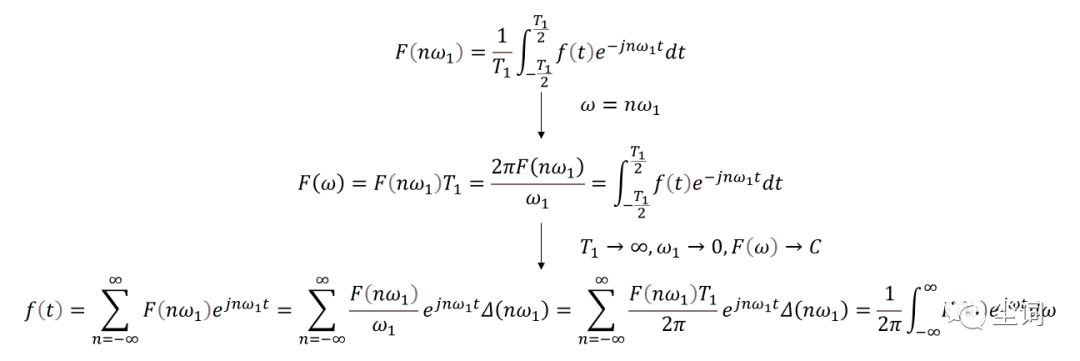
傅里葉變換:
傅里葉逆變換:
三角函數形式傅里葉變換:
(由幅度譜和相位譜奇偶性得到)
幅度雙邊譜左右對稱——幅度頻譜偶函數
相位譜關于原點對稱——相位頻譜奇函數

五、典型非周期信號的傅里葉變換
(一)單邊指數信號
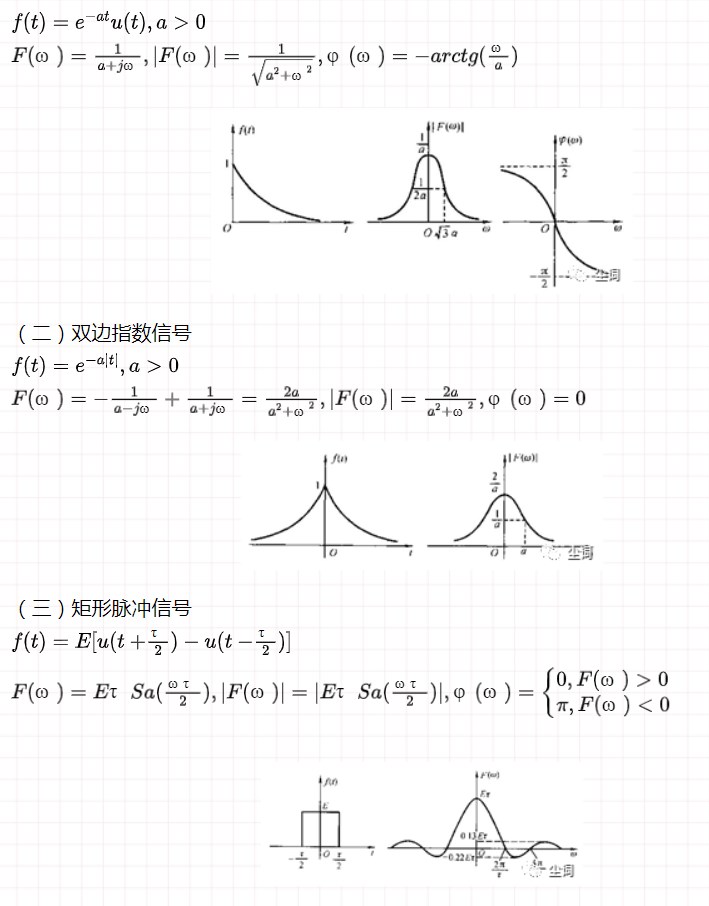
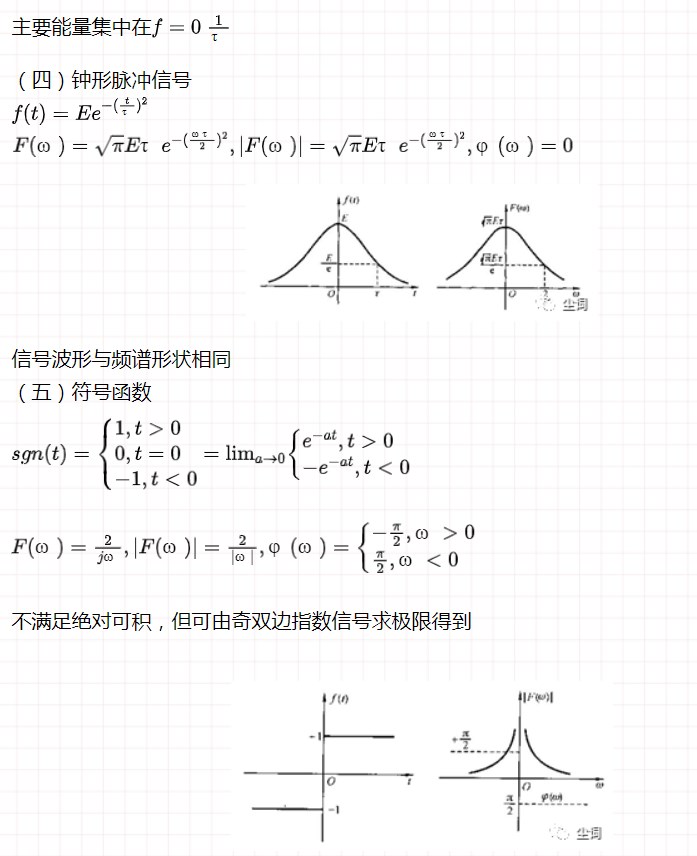
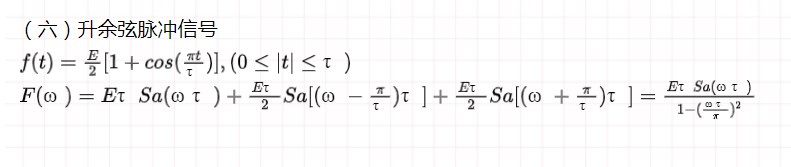
六、沖激函數和階躍函數的傅里葉變換
(一)沖激函數的傅里葉變換

聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
變換器
+關注
關注
17文章
2100瀏覽量
109345 -
低通濾波器
+關注
關注
14文章
474瀏覽量
47432 -
頻譜儀
+關注
關注
7文章
340瀏覽量
36072 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42612 -
直流信號
+關注
關注
0文章
39瀏覽量
8900
發布評論請先 登錄
相關推薦
傅里葉變換,建立信號頻譜
從本章開始由時域轉入變換域分析,首先討論傅里葉變換。傅里葉變換是在傅里葉級數正交函數展開的基礎上發展而產生的,這方面的問題也稱為傅里葉
發表于 08-05 11:49
?50次下載
傅里葉變換的時移特性
傅里葉變換的時移特性 傅里葉變換是一種非常重要的數學工具,可以將任何周期性信號或非周期性信號進行頻域分析,從而在通信、電子工程等領域中得到廣
短時傅里葉變換特點 短時傅里葉變換的意義
變化進行分析。與傅里葉變換相比,STFT可以捕捉信號在時間和頻率上的局部特征,是一種非常重要的信號處理技術。 STFT的特點 1. 局部性:
傅里葉變換公式理解
傅里葉變換公式理解 傅里葉變換是一種在數學、物理、工程和其他科學領域中常用的工具,它是一種將一個函數從時域轉換到頻域的方法。傅里葉變換可以將一個復雜的函數表示成一個頻域上各種周期函數的
傅里葉變換和離散傅里葉變換的關系
傅里葉變換和離散傅里葉變換的關系 傅里葉變換(Fourier Transform)是一種將時間域(或空間域)的信號轉換為頻率域(或波數域)的信號
傅里葉變換的定義 傅里葉變換的意義
連續傅里葉變換和離散傅里葉變換。最初傅里葉分析是作為熱過程的解析分析的工具被提出的。 傅里葉變換的意義主要體現在以下幾個方面: 1. 頻譜
傅里葉變換在信號處理中的應用
在現代通信和信號處理領域,傅里葉變換(FT)扮演著核心角色。它不僅幫助我們分析信號的頻率成分,還能用于濾波、壓縮和信號恢復等多種任務。
傅里葉變換的基本性質和定理
傅里葉變換是信號處理和分析中的一項基本工具,它能夠將一個信號從時間域(或空間域)轉換到頻率域。以下是傅里葉變換的基本性質和定理: 一、基本性




 傅里葉變換(對信號分析)(上)
傅里葉變換(對信號分析)(上)










評論