七、傅里葉變換的基本性質


八、卷積特性(卷積定理)
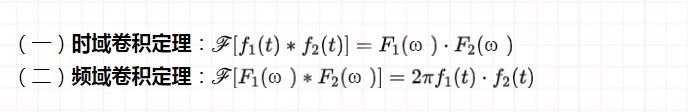
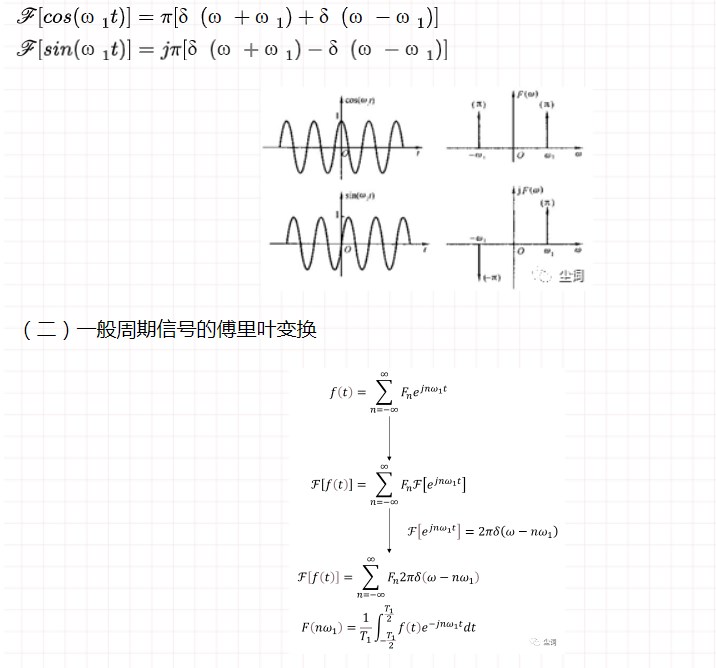
九、周期信號的傅里葉變換
雖然周期信號不滿足絕對可積條件,但認為沖激函數有意義下絕對可積稱為不必要的限制
頻移特性 ——余弦信號(周期)的傅里葉變換——導出其余信號的頻譜函數
(一)正弦、余弦信號的傅里葉變換

十、抽樣信號的傅里葉變換
(一)時域抽樣
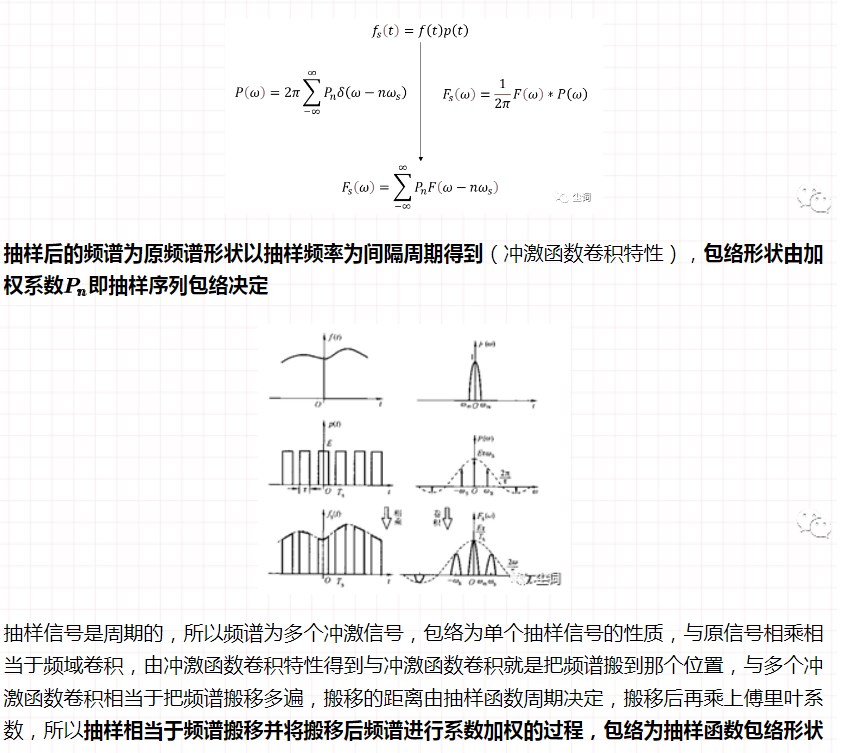
(二) 頻域抽樣 :頻域抽樣,時域周期延拓
時域頻域相對關系 : 離散——周期,連續——非周期 (反過來也一樣)
十一、抽樣定理

十二、總結
信號可以通過無限項正弦信號疊加而形成,也就是傅里葉級數的三角函數,但現實中疊加不能是無限的,相當于頻率加窗保留低頻項,扔掉高頻部分,因此產生了 吉布斯現象 。吉布斯現象的上沖是和窗函數(的時域波形,其旁瓣)有關的,從窗函數時頻域關系來解釋吉布斯現象。
傅里葉級數有三角函數形式、指數形式。傅里葉變換同樣三角函數形式、指數形式。兩者頻譜表示的內容不同,一為 幅度譜 ,一為 頻譜密度 ,但頻譜與頻譜密度之間有關系(差一個T)。
變換間頻譜的關系:


-
低通濾波器
+關注
關注
14文章
496瀏覽量
48264 -
時域分析
+關注
關注
0文章
41瀏覽量
11227 -
頻譜儀
+關注
關注
7文章
352瀏覽量
36887 -
傅里葉變換
+關注
關注
6文章
443瀏覽量
43161
發布評論請先 登錄



















評論