當我們涉及無線通信、信號處理和電子設備時，信號頻譜分析與功率譜密度是兩個至關重要的概念。它們幫助我們理解信號的特性、噪聲和頻率分布，從而優化通信系統、設計濾波器以及進行故障診斷。本文將初步探討信號頻譜分析與功率譜密度，一起理解其在工程和科技領域的應用。

信號頻譜分析

信號頻譜分析是將信號從時域轉換到頻域的過程，以便我們可以看清信號在各個頻率上的分布情況。頻譜圖顯示信號中各頻率分量的強度，幫助我們分析信號的頻率成分、調制方式以及可能的噪聲。常見的頻譜分析方法包括傅里葉變換、快速傅里葉變換（FFT）、小波變換等。

傅里葉變換：解析信號的頻域奧秘

傅里葉變換是信號處理領域中的基礎概念，它是將信號從時域轉換到頻域的重要方法。通過傅里葉變換，我們可以揭示信號的頻率成分，理解信號的周期性和振幅，從而在許多領域中實現廣泛的應用。本文將介紹傅里葉變換的基本原理、應用以及在科學和工程中的重要性。

傅里葉變換的原理

傅里葉變換是一種數學工具，用于將一個時域信號分解為多個不同頻率的正弦和余弦波的疊加。它的核心思想是，任何周期性信號都可以由不同頻率的正弦和余弦波組合而成。通過傅里葉變換，我們可以獲得信號在頻域中的頻率分布和振幅信息。

傅里葉變換的應用

1. 信號分析與濾波 ：傅里葉變換可以將信號從時域轉換到頻域，幫助我們分析信號的頻率成分。在濾波中，我們可以選擇特定頻率范圍內的分量，實現去除噪聲或突變的效果。
2. 圖像處理 ：傅里葉變換在圖像處理中也有廣泛應用。將圖像進行傅里葉變換后，可以將圖像分解為不同頻率的分量，實現圖像的平滑、銳化等處理。
3. 通信系統 ：傅里葉變換在通信系統中用于調制和解調信號。它可以將數字信號轉換為頻域信號，實現信號的傳輸和恢復。
4. 聲音處理 ：傅里葉變換在音頻處理中也有重要應用。將聲音信號進行傅里葉變換，可以分析聲音的頻率成分，實現音頻壓縮、降噪等處理。
5. 科學研究 ：傅里葉變換在科學研究中有廣泛應用，如天文學、地球物理學等領域。它可以幫助科學家分析復雜的信號數據，揭示隱藏的物理特性。

小結

傅里葉變換是一種強大的信號處理工具，可以將信號從時域轉換到頻域，揭示信號的頻率成分和特性。它在信號、圖像、聲音、通信等領域都有廣泛應用，幫助我們更好地分析、處理和理解數據。了解傅里葉變換的原理和應用，可以為科學研究、工程設計和技術創新提供有力支持。

快速傅里葉變換（FFT）：解析頻域的神奇算法

快速傅里葉變換（FFT）是一種高效的計算傅里葉變換的算法，它在信號處理、圖像處理、通信系統等領域中具有重要的應用。FFT算法的出現極大地提高了傅里葉變換的計算速度，使得我們能夠更快地從時域轉換到頻域，深入分析信號的頻率成分和特性。

FFT的基本原理

傅里葉變換是一種將信號從時域轉換到頻域的方法，但傳統的傅里葉變換算法的時間復雜度為O(n^2)，對于大規模的信號數據計算效率較低。FFT算法通過分治和迭代的思想，將復雜度降低到O(n log n)，極大地提高了計算速度。

FFT的基本思想是將信號分解為不同頻率的正弦和余弦波，然后將這些波的頻率分量合并計算，從而得到信號的頻譜。FFT算法通過將信號分解為多個子問題，逐層計算頻譜，最終得到完整的頻譜信息。

FFT的應用領域

1. 信號分析與濾波 ：在信號處理中，FFT可以幫助我們分析信號的頻率成分。通過將信號轉換到頻域，我們可以選擇特定頻率范圍內的分量，實現濾波和降噪的效果。
2. 通信系統 ：在通信系統中，FFT用于調制和解調信號。它可以將數字信號轉換為頻域信號，實現信號的傳輸和恢復。
3. 圖像處理 ：FFT在圖像處理中也有廣泛應用。通過對圖像進行FFT變換，可以分析圖像的頻率特性，實現圖像增強、去噪等處理。
4. 音頻處理 ：在音頻處理領域，FFT可以幫助我們分析音頻信號的頻率成分，實現音頻壓縮、均衡等處理。
5. 科學研究 ：FFT在科學研究中具有重要作用，如天文學、地球物理學等領域。它可以幫助科學家分析復雜的信號數據，揭示隱藏的物理特性。

FFT的實現與工具

FFT算法有多種實現方式，包括蝶形算法、快速拉賓算法等。在實際應用中，有許多開源工具和庫可以幫助我們進行FFT計算，如NumPy、MATLAB等。

快速傅里葉變換是一項強大的信號處理技術，通過高效的計算方法，可以從時域轉換到頻域，揭示信號的頻率分布和特性。它在多個領域中都有重要應用，幫助我們更好地理解和處理各種信號數據。

小波變換：從信號到頻譜的多尺度分析

在信號處理領域，小波變換是一種強大的工具，用于將信號從時域轉換到頻域，并在不同尺度上進行分析。與傳統的傅里葉變換或快速傅里葉變換不同，小波變換允許我們同時觀察信號的時間和頻率特性，提供了更詳細和全面的信息。本文將深入介紹小波變換的原理、應用以及其在現代科學和工程中的重要性。

小波變換的原理

小波變換使用一組稱為小波基函數的函數族，這些函數在時域和頻域上都具有局部性質。通過對信號進行小波變換，我們可以在時間和頻率上同時獲取信息，而不像傅里葉變換那樣僅僅提供頻率信息。小波基函數在時域上的伸縮和平移可以讓我們捕捉到信號中不同尺度的特征。

小波變換的應用

1. 信號分析與處理 ：小波變換在信號處理中廣泛應用，可以識別信號中的瞬態、脈沖、周期性等特征。通過對不同尺度下的小波系數進行分析，我們可以更好地了解信號的結構。
2. 圖像處理 ：小波變換可以應用于圖像處理，用于邊緣檢測、去噪、圖像壓縮等。由于小波變換的多尺度特性，它可以捕捉圖像中不同大小的特征。
3. 聲音處理 ：小波變換在音頻處理中有重要應用，可以分析聲音的諧波、噪聲、共振等特征，有助于音頻壓縮、降噪以及音頻特征提取。
4. 振動分析 ：在機械工程和結構健康監測中，小波變換可以幫助分析機械振動信號的頻率分量，用于故障診斷和狀態監測。
5. 金融分析 ：小波變換可用于分析金融時間序列數據，揭示不同時間尺度上的市場波動情況，以及趨勢和周期性變化。

小波變換與傅里葉變換的比較

盡管小波變換在許多應用中非常強大，但傅里葉變換仍然在某些情況下更加適用。以下是兩者之間的比較：

• 分辨率 ：小波變換具有多尺度分析的能力，可以捕捉信號的局部特征。傅里葉變換則提供信號的全局頻率信息。
• 計算效率 ：小波變換的計算相對復雜，尤其是連續小波變換。傅里葉變換的快速算法（FFT）可以在計算上更高效。
• 穩定性 ：小波變換對信號中的突變和瞬態有更好的穩定性，而傅里葉變換可能會產生頻譜泄漏。

小結

小波變換是信號處理領域中的重要工具，通過多尺度分析提供了更全面的信號信息。它在信號、圖像、聲音、振動等領域都有廣泛應用，幫助我們更好地理解和處理復雜的數據。了解小波變換的基本原理和應用，可以為工程、科研和技術創新提供強大的支持。

功率譜密度：揭示信號能量分布的重要工具

功率譜密度是信號處理中的一個關鍵概念，它描述了信號在不同頻率上的能量分布情況。通過分析信號的功率譜密度，我們可以深入了解信號的頻率成分和能量分布，從而在許多領域中做出更準確的判斷和決策。

功率譜密度的定義

功率譜密度是一個表示信號在不同頻率上的功率分布的函數。在頻譜分析中，我們通常使用傅里葉變換來將信號從時域轉換到頻域，然后計算信號的功率譜密度。功率譜密度可以告訴我們在不同頻率范圍內信號的功率大小。

為什么需要功率譜密度？

功率譜密度在許多應用中都扮演著重要的角色：

1. 信號特征分析 ：通過分析信號的功率譜密度，我們可以了解信號的頻率成分，從而判斷信號的類型、周期性等特征。
2. 通信系統 ：在通信系統中，功率譜密度可以幫助我們合理規劃信道帶寬和頻率分配，以提高通信質量和效率。
3. 噪聲分析 ：功率譜密度可以幫助我們分析信號中的噪聲分布情況，進而選擇合適的濾波方法來降低噪聲影響。
4. 振動分析 ：在振動領域，功率譜密度可以用來分析結構的振動特性，幫助工程師檢測結構的異常和問題。

計算功率譜密度

計算功率譜密度需要以下步驟：

1. 獲取信號數據 ：首先，需要獲取要分析的信號數據，可以是時間域的采樣數據。
2. 進行傅里葉變換 ：將信號數據進行傅里葉變換，將信號從時域轉換到頻域。
3. 計算信號功率 ：計算每個頻率分量上的信號功率，通常是對傅里葉變換結果的幅值平方。
4. 繪制功率譜密度圖 ：將不同頻率分量的功率繪制成圖表，可以是柱狀圖或曲線圖，展示信號在不同頻率上的能量分布情況。

應用案例

在無線通信中，功率譜密度可以幫助確定信號在頻域上的占用情況，從而避免不同信號之間的干擾。在音頻處理中，功率譜密度可以幫助我們分析音頻信號的頻譜特性，用于音頻編碼和解碼。

功率譜密度是一個有力的工具，能夠幫助我們深入了解信號在頻率域上的特性和能量分布情況。在信號處理、通信、工程等領域，它都具有廣泛的應用價值，幫助我們做出更準確的分析和決策。

python示例

頻譜

示例代碼：

复制import numpy as np
import matplotlib.pyplot as plt

# 生成一個信號，例如一個包含兩個頻率成分的正弦波
fs = 1000  # 采樣率
t = np.linspace(0, 1, fs, endpoint=False)
freq1 = 50  # 第一個頻率成分
freq2 = 150  # 第二個頻率成分
signal = np.sin(2 * np.pi * freq1 * t) + np.sin(2 * np.pi * freq2 * t)

# 使用快速傅里葉變換計算信號的頻譜
fft_result = np.fft.fft(signal)
freqs = np.fft.fftfreq(len(fft_result), 1/fs)
magnitude = np.abs(fft_result)

# 繪制原始信號和頻譜
plt.figure(figsize=(10, 6))

plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Original Signal')

plt.subplot(2, 1, 2)
plt.plot(freqs, magnitude)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.title('Spectrum')

plt.tight_layout()
plt.show()

輸出：

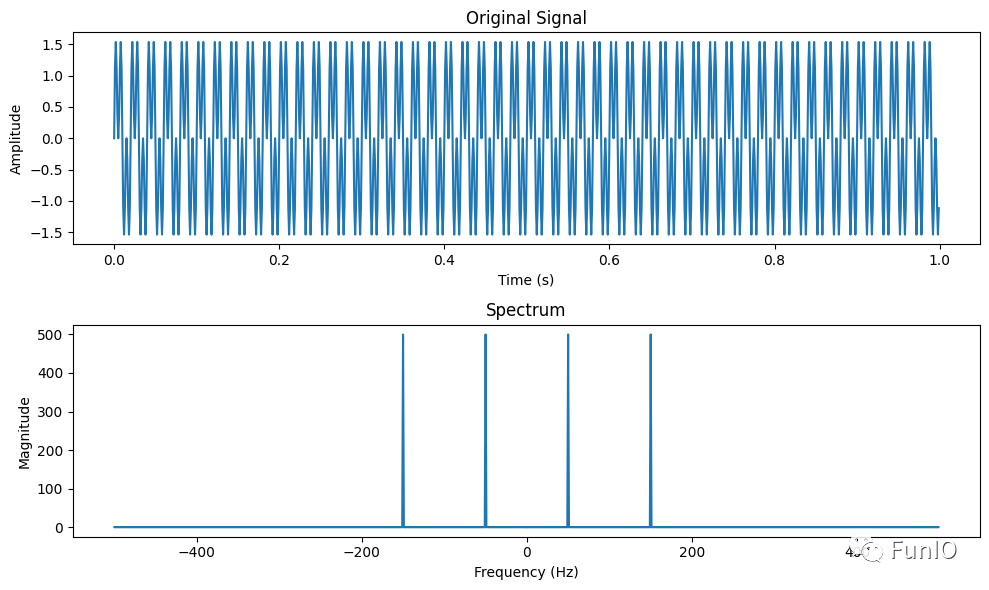
python頻譜分析示例

功率譜

示例代碼：

复制import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 生成一個示例信號（正弦波加噪聲）
fs = 1000  # 采樣率
t = np.arange(0, 10, 1/fs)  # 時間向量
freq = 50  # 正弦波頻率
signal_data = np.sin(2*np.pi*freq*t) + 0.5*np.random.randn(len(t))

# 計算功率譜密度
frequencies, power_density = signal.welch(signal_data, fs, nperseg=1024)

# 繪制功率譜密度圖
plt.figure(figsize=(10, 6))
plt.semilogy(frequencies, power_density)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power Density')
plt.title('Power Spectral Density')
plt.grid()
plt.show()

輸出：

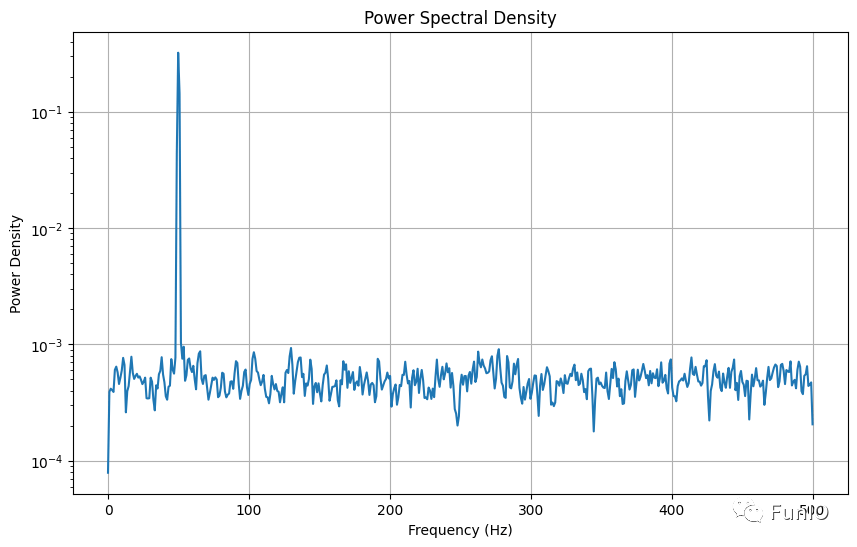
python功率譜分析示例

信號頻譜分析與功率譜密度在多個領域有重要應用：

1. 通信系統設計 ：在通信系統中，了解信號頻譜分布有助于選擇合適的調制方式和頻率分配，以最大化信號傳輸效率。
2. 無線電頻譜管理 ：在無線電頻譜管理中，監測各頻段的信號功率譜密度可以避免頻段之間的干擾。
3. 信號處理與濾波器設計 ：根據信號的功率譜密度特點，設計合適的濾波器以去除噪聲或選擇特定頻率分量。
4. 噪聲分析 ：功率譜密度分析有助于識別信號中的噪聲成分，并估計其影響。
5. 天文學與地震學 ：在這些領域，頻譜分析幫助科學家研究天體和地震信號的特性。
6. 信號故障診斷 ：通過分析信號的頻譜分布，可以識別信號中的異常或故障。

總結

信號頻譜分析與功率譜密度是理解信號特性、優化通信系統和進行故障診斷的關鍵工具。通過將信號從時域轉換到頻域，我們可以獲得信號在不同頻率上的分布情況，從而更好地理解信號的性質。在現代無線通信、信號處理和工程領域，頻譜分析與功率譜密度的應用無處不在，為我們帶來了許多技術和科學的突破。